ODE Discovery for Longitudinal Heterogeneous Treatment Effects Inference

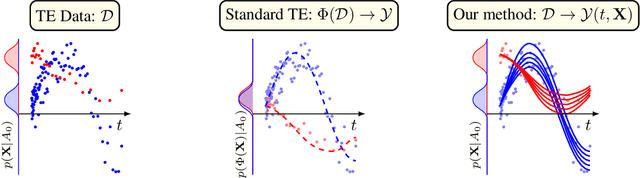
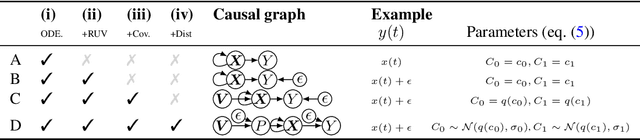
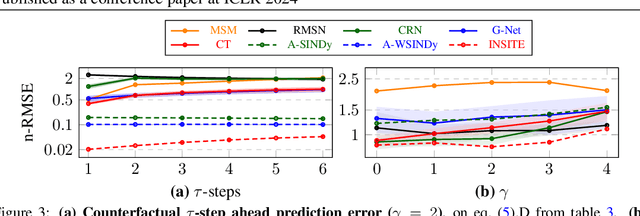
Inferring unbiased treatment effects has received widespread attention in the machine learning community. In recent years, our community has proposed numerous solutions in standard settings, high-dimensional treatment settings, and even longitudinal settings. While very diverse, the solution has mostly relied on neural networks for inference and simultaneous correction of assignment bias. New approaches typically build on top of previous approaches by proposing new (or refined) architectures and learning algorithms. However, the end result -- a neural-network-based inference machine -- remains unchallenged. In this paper, we introduce a different type of solution in the longitudinal setting: a closed-form ordinary differential equation (ODE). While we still rely on continuous optimization to learn an ODE, the resulting inference machine is no longer a neural network. Doing so yields several advantages such as interpretability, irregular sampling, and a different set of identification assumptions. Above all, we consider the introduction of a completely new type of solution to be our most important contribution as it may spark entirely new innovations in treatment effects in general. We facilitate this by formulating our contribution as a framework that can transform any ODE discovery method into a treatment effects method.

DAGnosis: Localized Identification of Data Inconsistencies using Structures

Identification and appropriate handling of inconsistencies in data at deployment time is crucial to reliably use machine learning models. While recent data-centric methods are able to identify such inconsistencies with respect to the training set, they suffer from two key limitations: (1) suboptimality in settings where features exhibit statistical independencies, due to their usage of compressive representations and (2) lack of localization to pin-point why a sample might be flagged as inconsistent, which is important to guide future data collection. We solve these two fundamental limitations using directed acyclic graphs (DAGs) to encode the training set's features probability distribution and independencies as a structure. Our method, called DAGnosis, leverages these structural interactions to bring valuable and insightful data-centric conclusions. DAGnosis unlocks the localization of the causes of inconsistencies on a DAG, an aspect overlooked by previous approaches. Moreover, we show empirically that leveraging these interactions (1) leads to more accurate conclusions in detecting inconsistencies, as well as (2) provides more detailed insights into why some samples are flagged.

Learning continuous-valued treatment effects through representation balancing

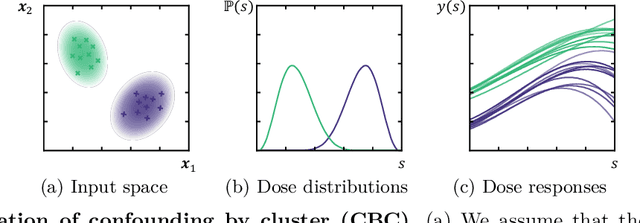
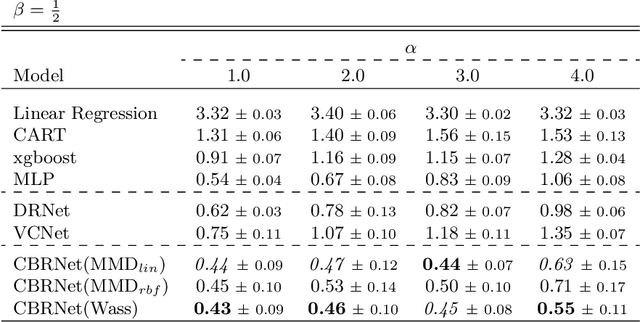
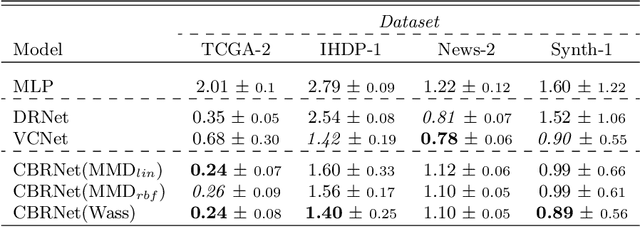
Estimating the effects of treatments with an associated dose on an instance's outcome, the "dose response", is relevant in a variety of domains, from healthcare to business, economics, and beyond. Such effects, also known as continuous-valued treatment effects, are typically estimated from observational data, which may be subject to dose selection bias. This means that the allocation of doses depends on pre-treatment covariates. Previous studies have shown that conventional machine learning approaches fail to learn accurate individual estimates of dose responses under the presence of dose selection bias. In this work, we propose CBRNet, a causal machine learning approach to estimate an individual dose response from observational data. CBRNet adopts the Neyman-Rubin potential outcome framework and extends the concept of balanced representation learning for overcoming selection bias to continuous-valued treatments. Our work is the first to apply representation balancing in a continuous-valued treatment setting. We evaluate our method on a newly proposed benchmark. Our experiments demonstrate CBRNet's ability to accurately learn treatment effects under selection bias and competitive performance with respect to other state-of-the-art methods.

Learning Representations without Compositional Assumptions

This paper addresses unsupervised representation learning on tabular data containing multiple views generated by distinct sources of measurement. Traditional methods, which tackle this problem using the multi-view framework, are constrained by predefined assumptions that assume feature sets share the same information and representations should learn globally shared factors. However, this assumption is not always valid for real-world tabular datasets with complex dependencies between feature sets, resulting in localized information that is harder to learn. To overcome this limitation, we propose a data-driven approach that learns feature set dependencies by representing feature sets as graph nodes and their relationships as learnable edges. Furthermore, we introduce LEGATO, a novel hierarchical graph autoencoder that learns a smaller, latent graph to aggregate information from multiple views dynamically. This approach results in latent graph components that specialize in capturing localized information from different regions of the input, leading to superior downstream performance.

Causal Deep Learning

Causality has the potential to truly transform the way we solve a large number of real-world problems. Yet, so far, its potential remains largely unlocked since most work so far requires strict assumptions which do not hold true in practice. To address this challenge and make progress in solving real-world problems, we propose a new way of thinking about causality - we call this causal deep learning. The framework which we propose for causal deep learning spans three dimensions: (1) a structural dimension, which allows incomplete causal knowledge rather than assuming either full or no causal knowledge; (2) a parametric dimension, which encompasses parametric forms which are typically ignored; and finally, (3) a temporal dimension, which explicitly allows for situations which capture exposure times or temporal structure. Together, these dimensions allow us to make progress on a variety of real-world problems by leveraging (sometimes incomplete) causal knowledge and/or combining diverse causal deep learning methods. This new framework also enables researchers to compare systematically across existing works as well as identify promising research areas which can lead to real-world impact.

Navigating causal deep learning

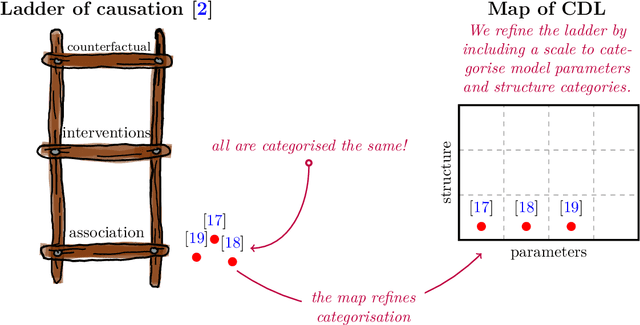
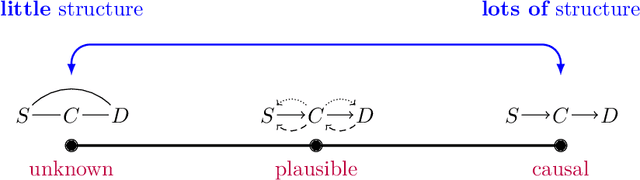
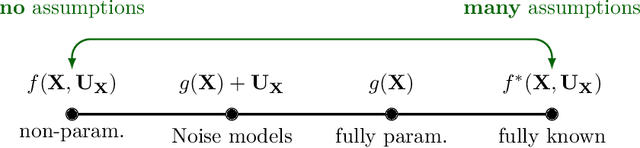
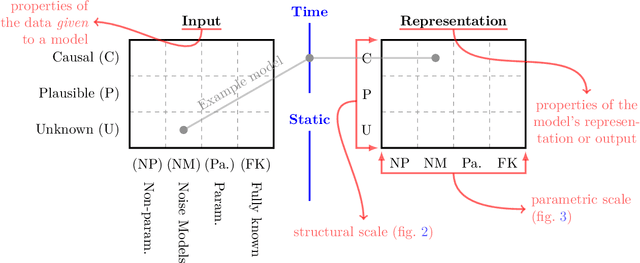
Causal deep learning (CDL) is a new and important research area in the larger field of machine learning. With CDL, researchers aim to structure and encode causal knowledge in the extremely flexible representation space of deep learning models. Doing so will lead to more informed, robust, and general predictions and inference -- which is important! However, CDL is still in its infancy. For example, it is not clear how we ought to compare different methods as they are so different in their output, the way they encode causal knowledge, or even how they represent this knowledge. This is a living paper that categorises methods in causal deep learning beyond Pearl's ladder of causation. We refine the rungs in Pearl's ladder, while also adding a separate dimension that categorises the parametric assumptions of both input and representation, arriving at the map of causal deep learning. Our map covers machine learning disciplines such as supervised learning, reinforcement learning, generative modelling and beyond. Our paradigm is a tool which helps researchers to: find benchmarks, compare methods, and most importantly: identify research gaps. With this work we aim to structure the avalanche of papers being published on causal deep learning. While papers on the topic are being published daily, our map remains fixed. We open-source our map for others to use as they see fit: perhaps to offer guidance in a related works section, or to better highlight the contribution of their paper.

Differentiable and Transportable Structure Learning

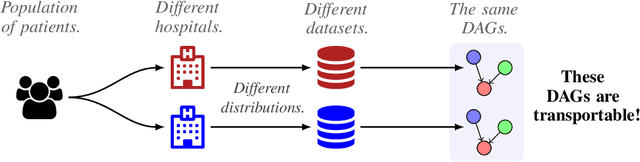
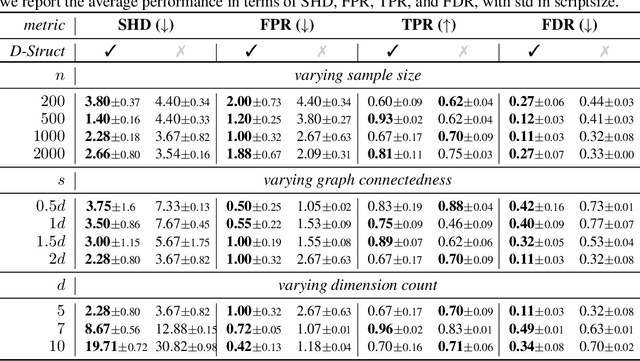
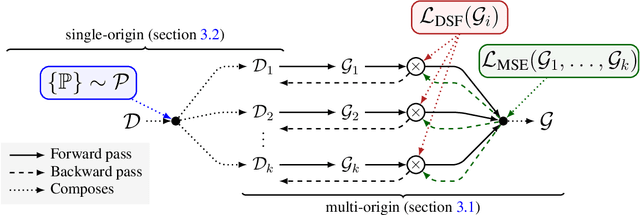
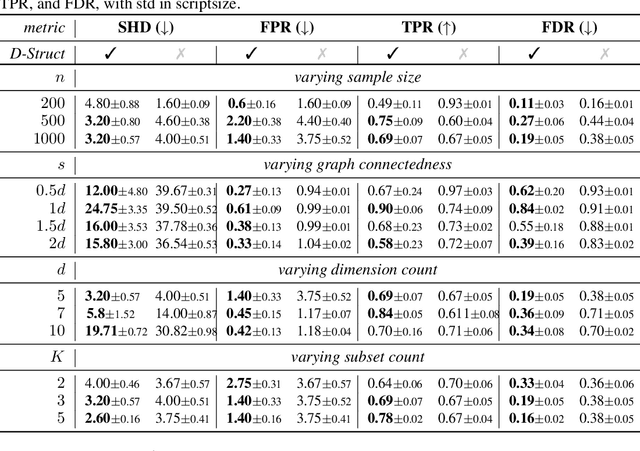
We are interested in unsupervised structure learning with a particular focus on directed acyclic graphical (DAG) models. Compute required to infer these structures is typically super-exponential in the amount of variables, as inference requires a sweep of a combinatorially large space of potential structures. That is, until recent advances allowed to search this space using a differentiable metric, drastically reducing search time. While this technique -- named NOTEARS -- is widely considered a seminal work in DAG-discovery, it concedes an important property in favour of differentiability: transportability. In our paper we introduce D-Struct which recovers transportability in the found structures through a novel architecture and loss function, while remaining completely differentiable. As D-Struct remains differentiable, one can easily adopt our method in differentiable architectures as was previously done with NOTEARS. In our experiments we empirically validate D-Struct with respect to edge accuracy and the structural Hamming distance.

Combining Observational and Randomized Data for Estimating Heterogeneous Treatment Effects

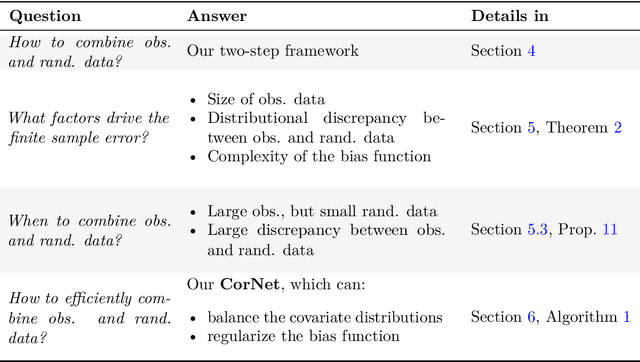
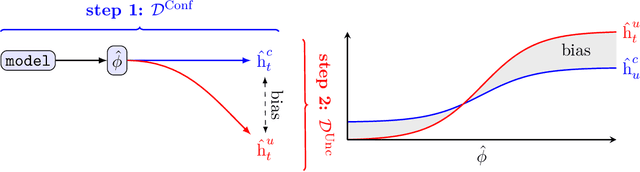
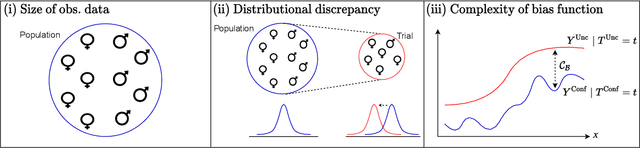
Estimating heterogeneous treatment effects is an important problem across many domains. In order to accurately estimate such treatment effects, one typically relies on data from observational studies or randomized experiments. Currently, most existing works rely exclusively on observational data, which is often confounded and, hence, yields biased estimates. While observational data is confounded, randomized data is unconfounded, but its sample size is usually too small to learn heterogeneous treatment effects. In this paper, we propose to estimate heterogeneous treatment effects by combining large amounts of observational data and small amounts of randomized data via representation learning. In particular, we introduce a two-step framework: first, we use observational data to learn a shared structure (in form of a representation); and then, we use randomized data to learn the data-specific structures. We analyze the finite sample properties of our framework and compare them to several natural baselines. As such, we derive conditions for when combining observational and randomized data is beneficial, and for when it is not. Based on this, we introduce a sample-efficient algorithm, called CorNet. We use extensive simulation studies to verify the theoretical properties of CorNet and multiple real-world datasets to demonstrate our method's superiority compared to existing methods.

To Impute or not to Impute? -- Missing Data in Treatment Effect Estimation

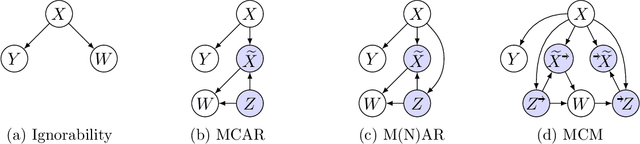
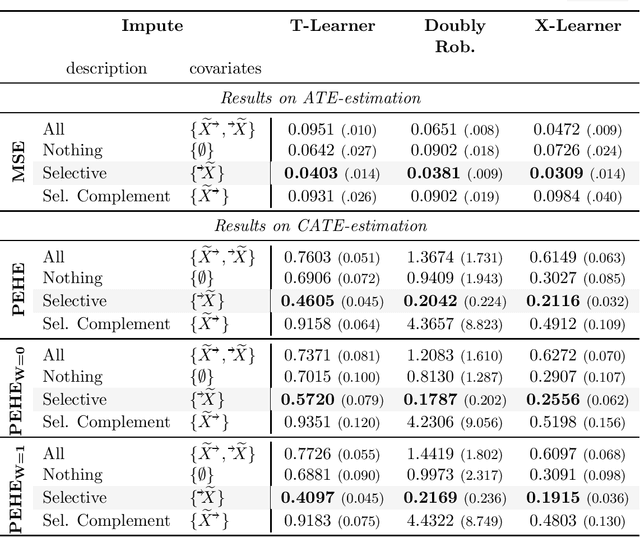
Missing data is a systemic problem in practical scenarios that causes noise and bias when estimating treatment effects. This makes treatment effect estimation from data with missingness a particularly tricky endeavour. A key reason for this is that standard assumptions on missingness are rendered insufficient due to the presence of an additional variable, treatment, besides the individual and the outcome. Having a treatment variable introduces additional complexity with respect to why some variables are missing that is not fully explored by previous work. In our work we identify a new missingness mechanism, which we term mixed confounded missingness (MCM), where some missingness determines treatment selection and other missingness is determined by treatment selection. Given MCM, we show that naively imputing all data leads to poor performing treatment effects models, as the act of imputation effectively removes information necessary to provide unbiased estimates. However, no imputation at all also leads to biased estimates, as missingness determined by treatment divides the population in distinct subpopulations, where estimates across these populations will be biased. Our solution is selective imputation, where we use insights from MCM to inform precisely which variables should be imputed and which should not. We empirically demonstrate how various learners benefit from selective imputation compared to other solutions for missing data.

Disentangled Counterfactual Recurrent Networks for Treatment Effect Inference over Time

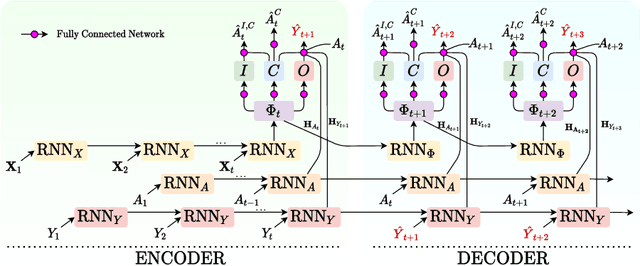
Choosing the best treatment-plan for each individual patient requires accurate forecasts of their outcome trajectories as a function of the treatment, over time. While large observational data sets constitute rich sources of information to learn from, they also contain biases as treatments are rarely assigned randomly in practice. To provide accurate and unbiased forecasts, we introduce the Disentangled Counterfactual Recurrent Network (DCRN), a novel sequence-to-sequence architecture that estimates treatment outcomes over time by learning representations of patient histories that are disentangled into three separate latent factors: a treatment factor, influencing only treatment selection; an outcome factor, influencing only the outcome; and a confounding factor, influencing both. With an architecture that is completely inspired by the causal structure of treatment influence over time, we advance forecast accuracy and disease understanding, as our architecture allows for practitioners to infer which patient features influence which part in a patient's trajectory, contrasting other approaches in this domain. We demonstrate that DCRN outperforms current state-of-the-art methods in forecasting treatment responses, on both real and simulated data.