Combining Observational and Randomized Data for Estimating Heterogeneous Treatment Effects
Paper and Code
Feb 25, 2022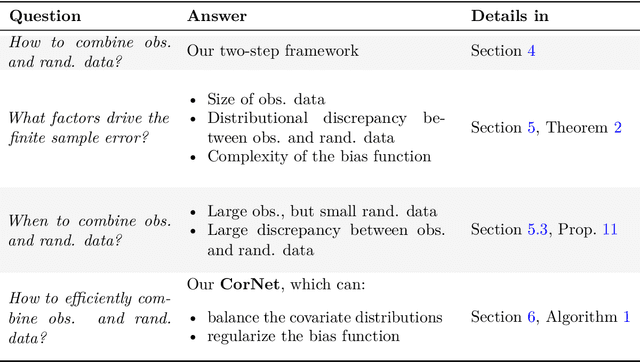
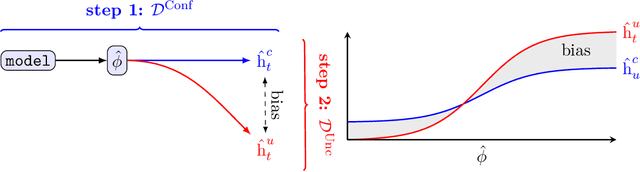
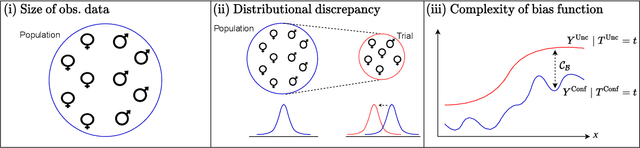

Estimating heterogeneous treatment effects is an important problem across many domains. In order to accurately estimate such treatment effects, one typically relies on data from observational studies or randomized experiments. Currently, most existing works rely exclusively on observational data, which is often confounded and, hence, yields biased estimates. While observational data is confounded, randomized data is unconfounded, but its sample size is usually too small to learn heterogeneous treatment effects. In this paper, we propose to estimate heterogeneous treatment effects by combining large amounts of observational data and small amounts of randomized data via representation learning. In particular, we introduce a two-step framework: first, we use observational data to learn a shared structure (in form of a representation); and then, we use randomized data to learn the data-specific structures. We analyze the finite sample properties of our framework and compare them to several natural baselines. As such, we derive conditions for when combining observational and randomized data is beneficial, and for when it is not. Based on this, we introduce a sample-efficient algorithm, called CorNet. We use extensive simulation studies to verify the theoretical properties of CorNet and multiple real-world datasets to demonstrate our method's superiority compared to existing methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge