Wasserstein GANs Work Because They Fail (to Approximate the Wasserstein Distance)
Paper and Code
Mar 05, 2021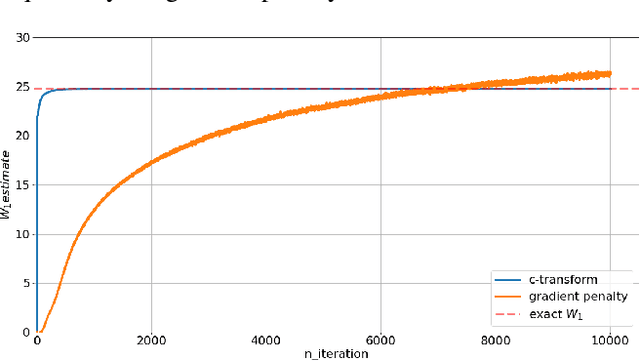
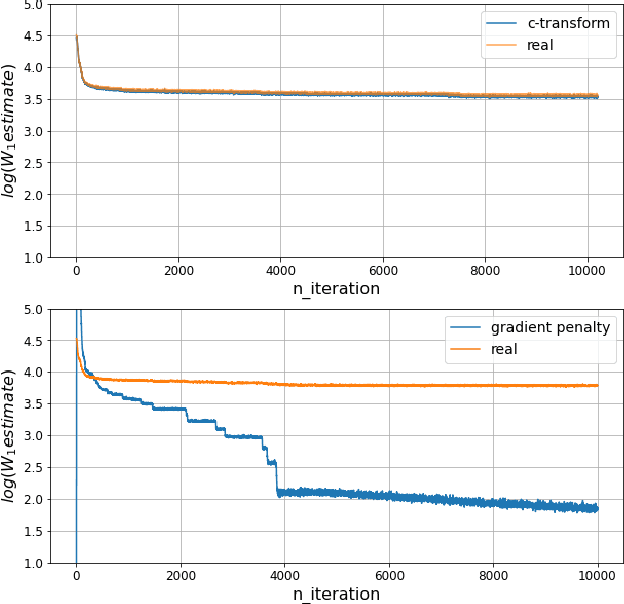

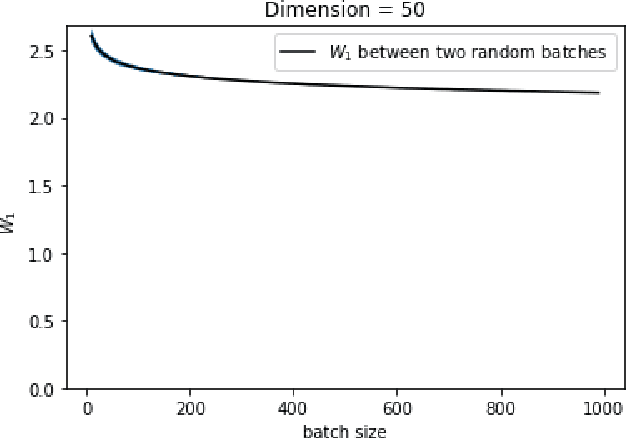
Wasserstein GANs are based on the idea of minimising the Wasserstein distance between a real and a generated distribution. We provide an in-depth mathematical analysis of differences between the theoretical setup and the reality of training Wasserstein GANs. In this work, we gather both theoretical and empirical evidence that the WGAN loss is not a meaningful approximation of the Wasserstein distance. Moreover, we argue that the Wasserstein distance is not even a desirable loss function for deep generative models, and conclude that the success of Wasserstein GANs can in truth be attributed to a failure to approximate the Wasserstein distance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge