Zero-Shot Context Generalization in Reinforcement Learning from Few Training Contexts

Deep reinforcement learning (DRL) has achieved remarkable success across multiple domains, including competitive games, natural language processing, and robotics. Despite these advancements, policies trained via DRL often struggle to generalize to evaluation environments with different parameters. This challenge is typically addressed by training with multiple contexts and/or by leveraging additional structure in the problem. However, obtaining sufficient training data across diverse contexts can be impractical in real-world applications. In this work, we consider contextual Markov decision processes (CMDPs) with transition and reward functions that exhibit regularity in context parameters. We introduce the context-enhanced Bellman equation (CEBE) to improve generalization when training on a single context. We prove both analytically and empirically that the CEBE yields a first-order approximation to the Q-function trained across multiple contexts. We then derive context sample enhancement (CSE) as an efficient data augmentation method for approximating the CEBE in deterministic control environments. We numerically validate the performance of CSE in simulation environments, showcasing its potential to improve generalization in DRL.

Demystifying Topological Message-Passing with Relational Structures: A Case Study on Oversquashing in Simplicial Message-Passing

Topological deep learning (TDL) has emerged as a powerful tool for modeling higher-order interactions in relational data. However, phenomena such as oversquashing in topological message-passing remain understudied and lack theoretical analysis. We propose a unifying axiomatic framework that bridges graph and topological message-passing by viewing simplicial and cellular complexes and their message-passing schemes through the lens of relational structures. This approach extends graph-theoretic results and algorithms to higher-order structures, facilitating the analysis and mitigation of oversquashing in topological message-passing networks. Through theoretical analysis and empirical studies on simplicial networks, we demonstrate the potential of this framework to advance TDL.

Stratified Non-Negative Tensor Factorization

Non-negative matrix factorization (NMF) and non-negative tensor factorization (NTF) decompose non-negative high-dimensional data into non-negative low-rank components. NMF and NTF methods are popular for their intrinsic interpretability and effectiveness on large-scale data. Recent work developed Stratified-NMF, which applies NMF to regimes where data may come from different sources (strata) with different underlying distributions, and seeks to recover both strata-dependent information and global topics shared across strata. Applying Stratified-NMF to multi-modal data requires flattening across modes, and therefore loses geometric structure contained implicitly within the tensor. To address this problem, we extend Stratified-NMF to the tensor setting by developing a multiplicative update rule and demonstrating the method on text and image data. We find that Stratified-NTF can identify interpretable topics with lower memory requirements than Stratified-NMF. We also introduce a regularized version of the method and demonstrate its effects on image data.

Narrative Analysis of True Crime Podcasts With Knowledge Graph-Augmented Large Language Models

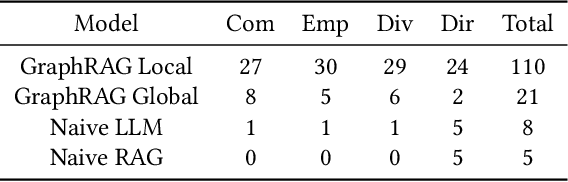
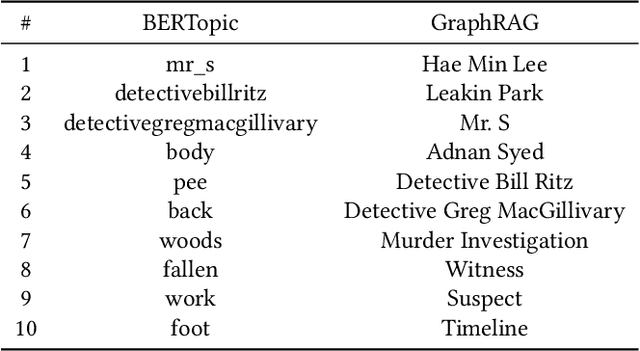
Narrative data spans all disciplines and provides a coherent model of the world to the reader or viewer. Recent advancement in machine learning and Large Language Models (LLMs) have enable great strides in analyzing natural language. However, Large language models (LLMs) still struggle with complex narrative arcs as well as narratives containing conflicting information. Recent work indicates LLMs augmented with external knowledge bases can improve the accuracy and interpretability of the resulting models. In this work, we analyze the effectiveness of applying knowledge graphs (KGs) in understanding true-crime podcast data from both classical Natural Language Processing (NLP) and LLM approaches. We directly compare KG-augmented LLMs (KGLLMs) with classical methods for KG construction, topic modeling, and sentiment analysis. Additionally, the KGLLM allows us to query the knowledge base in natural language and test its ability to factually answer questions. We examine the robustness of the model to adversarial prompting in order to test the model's ability to deal with conflicting information. Finally, we apply classical methods to understand more subtle aspects of the text such as the use of hearsay and sentiment in narrative construction and propose future directions. Our results indicate that KGLLMs outperform LLMs on a variety of metrics, are more robust to adversarial prompts, and are more capable of summarizing the text into topics.

Spectroscopy-Guided Discovery of Three-Dimensional Structures of Disordered Materials with Diffusion Models

The ability to rapidly develop materials with desired properties has a transformative impact on a broad range of emerging technologies. In this work, we introduce a new framework based on the diffusion model, a recent generative machine learning method to predict 3D structures of disordered materials from a target property. For demonstration, we apply the model to identify the atomic structures of amorphous carbons ($a$-C) as a representative material system from the target X-ray absorption near edge structure (XANES) spectra--a common experimental technique to probe atomic structures of materials. We show that conditional generation guided by XANES spectra reproduces key features of the target structures. Furthermore, we show that our model can steer the generative process to tailor atomic arrangements for a specific XANES spectrum. Finally, our generative model exhibits a remarkable scale-agnostic property, thereby enabling generation of realistic, large-scale structures through learning from a small-scale dataset (i.e., with small unit cells). Our work represents a significant stride in bridging the gap between materials characterization and atomic structure determination; in addition, it can be leveraged for materials discovery in exploring various material properties as targeted.

Stratified-NMF for Heterogeneous Data

Non-negative matrix factorization (NMF) is an important technique for obtaining low dimensional representations of datasets. However, classical NMF does not take into account data that is collected at different times or in different locations, which may exhibit heterogeneity. We resolve this problem by solving a modified NMF objective, Stratified-NMF, that simultaneously learns strata-dependent statistics and a shared topics matrix. We develop multiplicative update rules for this novel objective and prove convergence of the objective. Then, we experiment on synthetic data to demonstrate the efficiency and accuracy of the method. Lastly, we apply our method to three real world datasets and empirically investigate their learned features.

Efficient Algorithms for the CCA Family: Unconstrained Objectives with Unbiased Gradients

The Canonical Correlation Analysis (CCA) family of methods is foundational in multi-view learning. Regularised linear CCA methods can be seen to generalise Partial Least Squares (PLS) and unified with a Generalized Eigenvalue Problem (GEP) framework. However, classical algorithms for these linear methods are computationally infeasible for large-scale data. Extensions to Deep CCA show great promise, but current training procedures are slow and complicated. First we propose a novel unconstrained objective that characterizes the top subspace of GEPs. Our core contribution is a family of fast algorithms for stochastic PLS, stochastic CCA, and Deep CCA, simply obtained by applying stochastic gradient descent (SGD) to the corresponding CCA objectives. These methods show far faster convergence and recover higher correlations than the previous state-of-the-art on all standard CCA and Deep CCA benchmarks. This speed allows us to perform a first-of-its-kind PLS analysis of an extremely large biomedical dataset from the UK Biobank, with over 33,000 individuals and 500,000 variants. Finally, we not only match the performance of `CCA-family' Self-Supervised Learning (SSL) methods on CIFAR-10 and CIFAR-100 with minimal hyper-parameter tuning, but also establish the first solid theoretical links to classical CCA, laying the groundwork for future insights.

Novel Batch Active Learning Approach and Its Application to Synthetic Aperture Radar Datasets

Active learning improves the performance of machine learning methods by judiciously selecting a limited number of unlabeled data points to query for labels, with the aim of maximally improving the underlying classifier's performance. Recent gains have been made using sequential active learning for synthetic aperture radar (SAR) data arXiv:2204.00005. In each iteration, sequential active learning selects a query set of size one while batch active learning selects a query set of multiple datapoints. While batch active learning methods exhibit greater efficiency, the challenge lies in maintaining model accuracy relative to sequential active learning methods. We developed a novel, two-part approach for batch active learning: Dijkstra's Annulus Core-Set (DAC) for core-set generation and LocalMax for batch sampling. The batch active learning process that combines DAC and LocalMax achieves nearly identical accuracy as sequential active learning but is more efficient, proportional to the batch size. As an application, a pipeline is built based on transfer learning feature embedding, graph learning, DAC, and LocalMax to classify the FUSAR-Ship and OpenSARShip datasets. Our pipeline outperforms the state-of-the-art CNN-based methods.

Multi-modal Variational Autoencoders for normative modelling across multiple imaging modalities

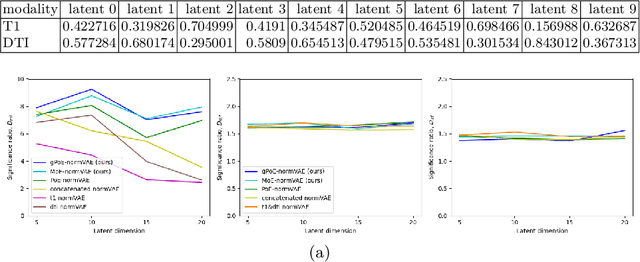
One of the challenges of studying common neurological disorders is disease heterogeneity including differences in causes, neuroimaging characteristics, comorbidities, or genetic variation. Normative modelling has become a popular method for studying such cohorts where the 'normal' behaviour of a physiological system is modelled and can be used at subject level to detect deviations relating to disease pathology. For many heterogeneous diseases, we expect to observe abnormalities across a range of neuroimaging and biological variables. However, thus far, normative models have largely been developed for studying a single imaging modality. We aim to develop a multi-modal normative modelling framework where abnormality is aggregated across variables of multiple modalities and is better able to detect deviations than uni-modal baselines. We propose two multi-modal VAE normative models to detect subject level deviations across T1 and DTI data. Our proposed models were better able to detect diseased individuals, capture disease severity, and correlate with patient cognition than baseline approaches. We also propose a multivariate latent deviation metric, measuring deviations from the joint latent space, which outperformed feature-based metrics.

Score-based denoising for atomic structure identification

We propose an accurate method for removing thermal vibrations that complicate the task of analyzing complex dynamics in atomistic simulation of condensed matter. Our method iteratively subtracts thermal noises or perturbations in atomic positions using a denoising score function trained on synthetically noised but otherwise perfect crystal lattices. The resulting denoised structures clearly reveal underlying crystal order while retaining disorder associated with crystal defects. Purely geometric, agnostic to interatomic potentials, and trained without inputs from explicit simulations, our denoiser can be applied to simulation data generated from vastly different interatomic interactions. Followed by a simple phase classification tool such as the Common Neighbor Analysis, the denoiser outperforms other existing methods and reaches perfect classification accuracy on a recently proposed benchmark dataset consisting of perturbed crystal structures (DC3). Demonstrated here in a wide variety of atomistic simulation contexts, the denoiser is general, robust, and readily extendable to delineate order from disorder in structurally and chemically complex materials.