Efficient Algorithms for the CCA Family: Unconstrained Objectives with Unbiased Gradients

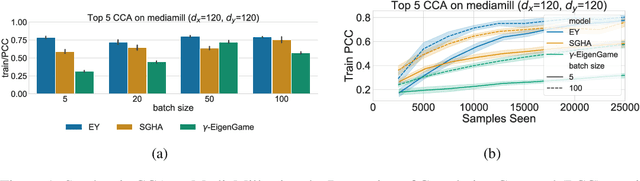
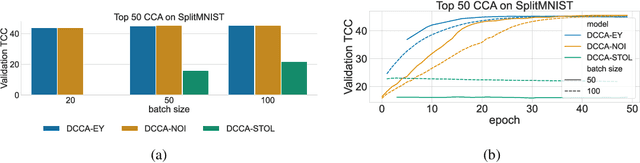
The Canonical Correlation Analysis (CCA) family of methods is foundational in multi-view learning. Regularised linear CCA methods can be seen to generalise Partial Least Squares (PLS) and unified with a Generalized Eigenvalue Problem (GEP) framework. However, classical algorithms for these linear methods are computationally infeasible for large-scale data. Extensions to Deep CCA show great promise, but current training procedures are slow and complicated. First we propose a novel unconstrained objective that characterizes the top subspace of GEPs. Our core contribution is a family of fast algorithms for stochastic PLS, stochastic CCA, and Deep CCA, simply obtained by applying stochastic gradient descent (SGD) to the corresponding CCA objectives. These methods show far faster convergence and recover higher correlations than the previous state-of-the-art on all standard CCA and Deep CCA benchmarks. This speed allows us to perform a first-of-its-kind PLS analysis of an extremely large biomedical dataset from the UK Biobank, with over 33,000 individuals and 500,000 variants. Finally, we not only match the performance of `CCA-family' Self-Supervised Learning (SSL) methods on CIFAR-10 and CIFAR-100 with minimal hyper-parameter tuning, but also establish the first solid theoretical links to classical CCA, laying the groundwork for future insights.