Improving Neuropathological Reconstruction Fidelity via AI Slice Imputation

Neuropathological analyses benefit from spatially precise volumetric reconstructions that enhance anatomical delineation and improve morphometric accuracy. Our prior work has shown the feasibility of reconstructing 3D brain volumes from 2D dissection photographs. However these outputs sometimes exhibit coarse, overly smooth reconstructions of structures, especially under high anisotropy (i.e., reconstructions from thick slabs). Here, we introduce a computationally efficient super-resolution step that imputes slices to generate anatomically consistent isotropic volumes from anisotropic 3D reconstructions of dissection photographs. By training on domain-randomized synthetic data, we ensure that our method generalizes across dissection protocols and remains robust to large slab thicknesses. The imputed volumes yield improved automated segmentations, achieving higher Dice scores, particularly in cortical and white matter regions. Validation on surface reconstruction and atlas registration tasks demonstrates more accurate cortical surfaces and MRI registration. By enhancing the resolution and anatomical fidelity of photograph-based reconstructions, our approach strengthens the bridge between neuropathology and neuroimaging. Our method is publicly available at https://surfer.nmr.mgh.harvard.edu/fswiki/mri_3d_photo_recon

Conditional diffusion models for guided anomaly detection in brain images using fluid-driven anomaly randomization

Supervised machine learning has enabled accurate pathology detection in brain MRI, but requires training data from diseased subjects that may not be readily available in some scenarios, for example, in the case of rare diseases. Reconstruction-based unsupervised anomaly detection, in particular using diffusion models, has gained popularity in the medical field as it allows for training on healthy images alone, eliminating the need for large disease-specific cohorts. These methods assume that a model trained on normal data cannot accurately represent or reconstruct anomalies. However, this assumption often fails with models failing to reconstruct healthy tissue or accurately reconstruct abnormal regions i.e., failing to remove anomalies. In this work, we introduce a novel conditional diffusion model framework for anomaly detection and healthy image reconstruction in brain MRI. Our weakly supervised approach integrates synthetically generated pseudo-pathology images into the modeling process to better guide the reconstruction of healthy images. To generate these pseudo-pathologies, we apply fluid-driven anomaly randomization to augment real pathology segmentation maps from an auxiliary dataset, ensuring that the synthetic anomalies are both realistic and anatomically coherent. We evaluate our model's ability to detect pathology, using both synthetic anomaly datasets and real pathology from the ATLAS dataset. In our extensive experiments, our model: (i) consistently outperforms variational autoencoders, and conditional and unconditional latent diffusion; and (ii) surpasses on most datasets, the performance of supervised inpainting methods with access to paired diseased/healthy images.

Disentangled Diffusion Autoencoder for Harmonization of Multi-site Neuroimaging Data

Combining neuroimaging datasets from multiple sites and scanners can help increase statistical power and thus provide greater insight into subtle neuroanatomical effects. However, site-specific effects pose a challenge by potentially obscuring the biological signal and introducing unwanted variance. Existing harmonization techniques, which use statistical models to remove such effects, have been shown to incompletely remove site effects while also failing to preserve biological variability. More recently, generative models using GANs or autoencoder-based approaches, have been proposed for site adjustment. However, such methods are known for instability during training or blurry image generation. In recent years, diffusion models have become increasingly popular for their ability to generate high-quality synthetic images. In this work, we introduce the disentangled diffusion autoencoder (DDAE), a novel diffusion model designed for controlling specific aspects of an image. We apply the DDAE to the task of harmonizing MR images by generating high-quality site-adjusted images that preserve biological variability. We use data from 7 different sites and demonstrate the DDAE's superiority in generating high-resolution, harmonized 2D MR images over previous approaches. As far as we are aware, this work marks the first diffusion-based model for site adjustment of neuroimaging data.

A tutorial on multi-view autoencoders using the multi-view-AE library

There has been a growing interest in recent years in modelling multiple modalities (or views) of data to for example, understand the relationship between modalities or to generate missing data. Multi-view autoencoders have gained significant traction for their adaptability and versatility in modelling multi-modal data, demonstrating an ability to tailor their approach to suit the characteristics of the data at hand. However, most multi-view autoencoders have inconsistent notation and are often implemented using different coding frameworks. To address this, we present a unified mathematical framework for multi-view autoencoders, consolidating their formulations. Moreover, we offer insights into the motivation and theoretical advantages of each model. To facilitate accessibility and practical use, we extend the documentation and functionality of the previously introduced \texttt{multi-view-AE} library. This library offers Python implementations of numerous multi-view autoencoder models, presented within a user-friendly framework. Through benchmarking experiments, we evaluate our implementations against previous ones, demonstrating comparable or superior performance. This work aims to establish a cohesive foundation for multi-modal modelling, serving as a valuable educational resource in the field.

Efficient Algorithms for the CCA Family: Unconstrained Objectives with Unbiased Gradients

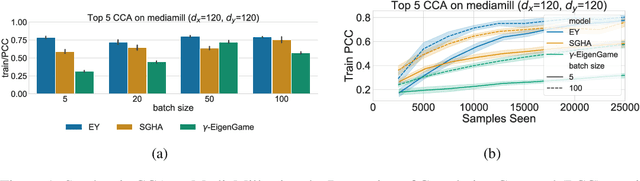
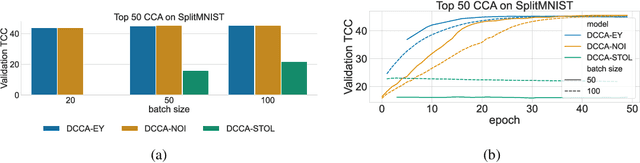
The Canonical Correlation Analysis (CCA) family of methods is foundational in multi-view learning. Regularised linear CCA methods can be seen to generalise Partial Least Squares (PLS) and unified with a Generalized Eigenvalue Problem (GEP) framework. However, classical algorithms for these linear methods are computationally infeasible for large-scale data. Extensions to Deep CCA show great promise, but current training procedures are slow and complicated. First we propose a novel unconstrained objective that characterizes the top subspace of GEPs. Our core contribution is a family of fast algorithms for stochastic PLS, stochastic CCA, and Deep CCA, simply obtained by applying stochastic gradient descent (SGD) to the corresponding CCA objectives. These methods show far faster convergence and recover higher correlations than the previous state-of-the-art on all standard CCA and Deep CCA benchmarks. This speed allows us to perform a first-of-its-kind PLS analysis of an extremely large biomedical dataset from the UK Biobank, with over 33,000 individuals and 500,000 variants. Finally, we not only match the performance of `CCA-family' Self-Supervised Learning (SSL) methods on CIFAR-10 and CIFAR-100 with minimal hyper-parameter tuning, but also establish the first solid theoretical links to classical CCA, laying the groundwork for future insights.

Multi-modal Variational Autoencoders for normative modelling across multiple imaging modalities

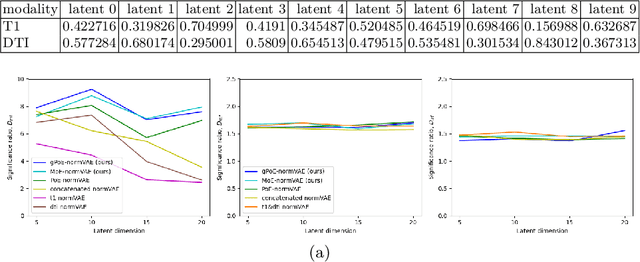
One of the challenges of studying common neurological disorders is disease heterogeneity including differences in causes, neuroimaging characteristics, comorbidities, or genetic variation. Normative modelling has become a popular method for studying such cohorts where the 'normal' behaviour of a physiological system is modelled and can be used at subject level to detect deviations relating to disease pathology. For many heterogeneous diseases, we expect to observe abnormalities across a range of neuroimaging and biological variables. However, thus far, normative models have largely been developed for studying a single imaging modality. We aim to develop a multi-modal normative modelling framework where abnormality is aggregated across variables of multiple modalities and is better able to detect deviations than uni-modal baselines. We propose two multi-modal VAE normative models to detect subject level deviations across T1 and DTI data. Our proposed models were better able to detect diseased individuals, capture disease severity, and correlate with patient cognition than baseline approaches. We also propose a multivariate latent deviation metric, measuring deviations from the joint latent space, which outperformed feature-based metrics.

A Generalized EigenGame with Extensions to Multiview Representation Learning

Generalized Eigenvalue Problems (GEPs) encompass a range of interesting dimensionality reduction methods. Development of efficient stochastic approaches to these problems would allow them to scale to larger datasets. Canonical Correlation Analysis (CCA) is one example of a GEP for dimensionality reduction which has found extensive use in problems with two or more views of the data. Deep learning extensions of CCA require large mini-batch sizes, and therefore large memory consumption, in the stochastic setting to achieve good performance and this has limited its application in practice. Inspired by the Generalized Hebbian Algorithm, we develop an approach to solving stochastic GEPs in which all constraints are softly enforced by Lagrange multipliers. Then by considering the integral of this Lagrangian function, its pseudo-utility, and inspired by recent formulations of Principal Components Analysis and GEPs as games with differentiable utilities, we develop a game-theory inspired approach to solving GEPs. We show that our approaches share much of the theoretical grounding of the previous Hebbian and game theoretic approaches for the linear case but our method permits extension to general function approximators like neural networks for certain GEPs for dimensionality reduction including CCA which means our method can be used for deep multiview representation learning. We demonstrate the effectiveness of our method for solving GEPs in the stochastic setting using canonical multiview datasets and demonstrate state-of-the-art performance for optimizing Deep CCA.