Oversquashing in GNNs through the lens of information contraction and graph expansion

The quality of signal propagation in message-passing graph neural networks (GNNs) strongly influences their expressivity as has been observed in recent works. In particular, for prediction tasks relying on long-range interactions, recursive aggregation of node features can lead to an undesired phenomenon called "oversquashing". We present a framework for analyzing oversquashing based on information contraction. Our analysis is guided by a model of reliable computation due to von Neumann that lends a new insight into oversquashing as signal quenching in noisy computation graphs. Building on this, we propose a graph rewiring algorithm aimed at alleviating oversquashing. Our algorithm employs a random local edge flip primitive motivated by an expander graph construction. We compare the spectral expansion properties of our algorithm with that of an existing curvature-based non-local rewiring strategy. Synthetic experiments show that while our algorithm in general has a slower rate of expansion, it is overall computationally cheaper, preserves the node degrees exactly and never disconnects the graph.

Learning curves for Gaussian process regression with power-law priors and targets

We study the power-law asymptotics of learning curves for Gaussian process regression (GPR). When the eigenspectrum of the prior decays with rate $\alpha$ and the eigenexpansion coefficients of the target function decay with rate $\beta$, we show that the generalization error behaves as $\tilde O(n^{\max\{\frac{1}{\alpha}-1, \frac{1-2\beta}{\alpha}\}})$ with high probability over the draw of $n$ input samples. Under similar assumptions, we show that the generalization error of kernel ridge regression (KRR) has the same asymptotics. Infinitely wide neural networks can be related to KRR with respect to the neural tangent kernel (NTK), which in several cases is known to have a power-law spectrum. Hence our methods can be applied to study the generalization error of infinitely wide neural networks. We present toy experiments demonstrating the theory.

Information Complexity and Generalization Bounds

We present a unifying picture of PAC-Bayesian and mutual information-based upper bounds on the generalization error of randomized learning algorithms. As we show, Tong Zhang's information exponential inequality (IEI) gives a general recipe for constructing bounds of both flavors. We show that several important results in the literature can be obtained as simple corollaries of the IEI under different assumptions on the loss function. Moreover, we obtain new bounds for data-dependent priors and unbounded loss functions. Optimizing the bounds gives rise to variants of the Gibbs algorithm, for which we discuss two practical examples for learning with neural networks, namely, Entropy- and PAC-Bayes- SGD. Further, we use an Occam's factor argument to show a PAC-Bayesian bound that incorporates second-order curvature information of the training loss.

The Variational Deficiency Bottleneck

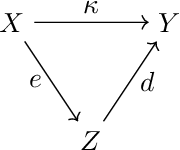
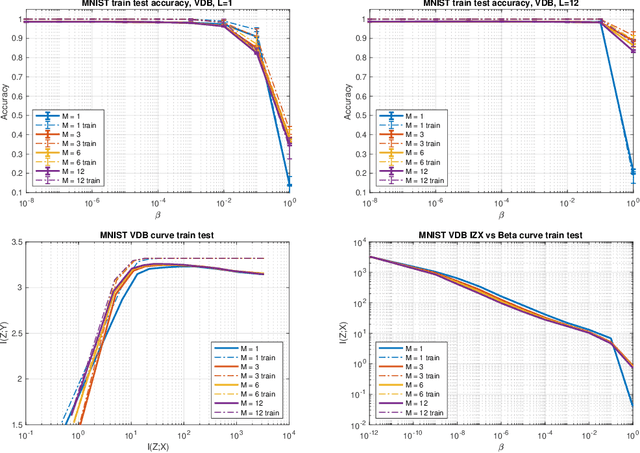
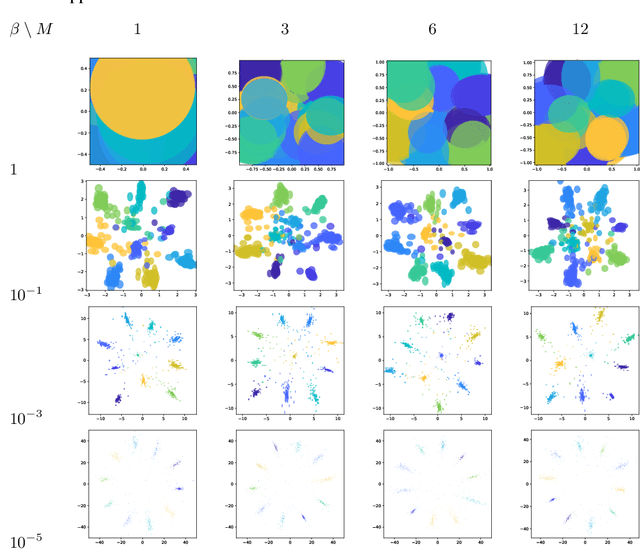
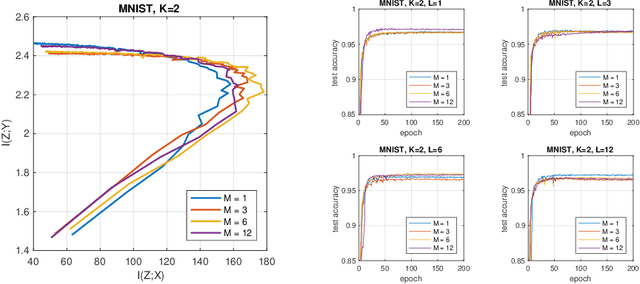
We introduce a bottleneck method for learning data representations based on channel deficiency, rather than the more traditional information sufficiency. A variational upper bound allows us to implement this method efficiently. The bound itself is bounded above by the variational information bottleneck objective, and the two methods coincide in the regime of single-shot Monte Carlo approximations. The notion of deficiency provides a principled way of approximating complicated channels by relatively simpler ones. The deficiency of one channel w.r.t. another has an operational interpretation in terms of the optimal risk gap of decision problems, capturing classification as a special case. Unsupervised generalizations are possible, such as the deficiency autoencoder, which can also be formulated in a variational form. Experiments demonstrate that the deficiency bottleneck can provide advantages in terms of minimal sufficiency as measured by information bottleneck curves, while retaining a good test performance in classification and reconstruction tasks.