The Variational Deficiency Bottleneck

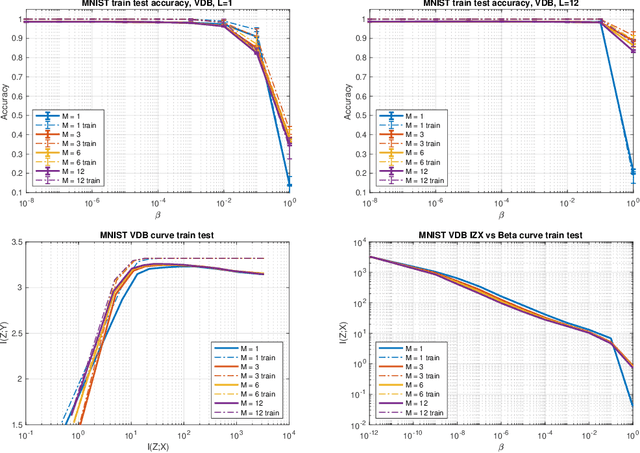
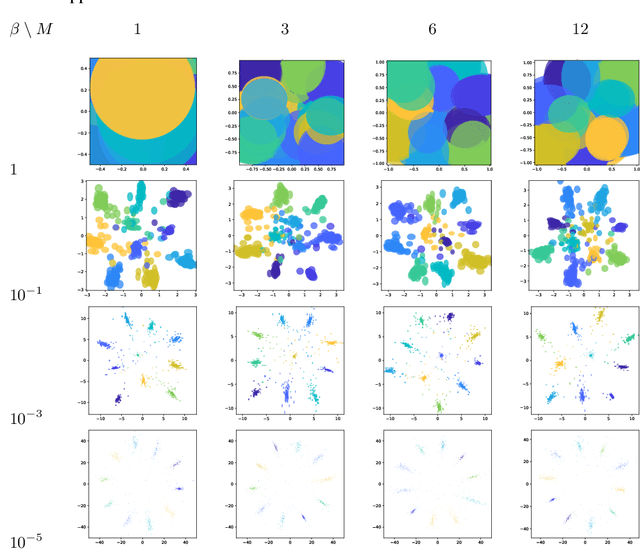
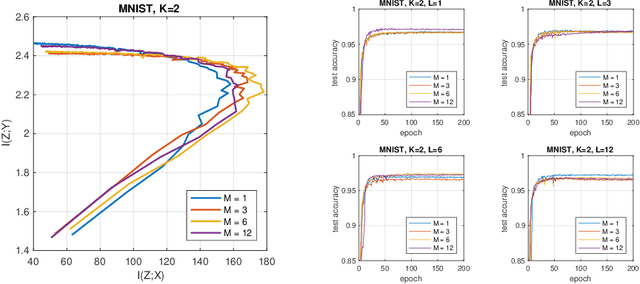
We introduce a bottleneck method for learning data representations based on channel deficiency, rather than the more traditional information sufficiency. A variational upper bound allows us to implement this method efficiently. The bound itself is bounded above by the variational information bottleneck objective, and the two methods coincide in the regime of single-shot Monte Carlo approximations. The notion of deficiency provides a principled way of approximating complicated channels by relatively simpler ones. The deficiency of one channel w.r.t. another has an operational interpretation in terms of the optimal risk gap of decision problems, capturing classification as a special case. Unsupervised generalizations are possible, such as the deficiency autoencoder, which can also be formulated in a variational form. Experiments demonstrate that the deficiency bottleneck can provide advantages in terms of minimal sufficiency as measured by information bottleneck curves, while retaining a good test performance in classification and reconstruction tasks.