Towards Understanding How Transformer Perform Multi-step Reasoning with Matching Operation

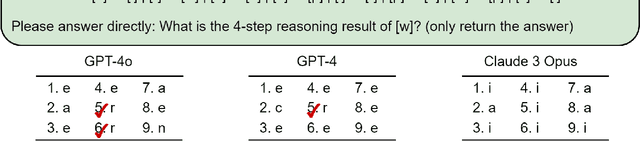
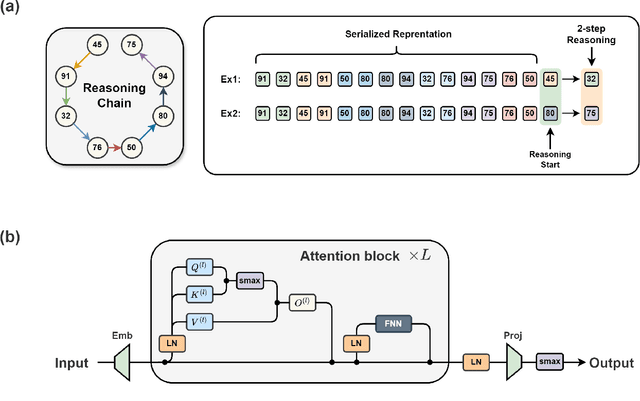
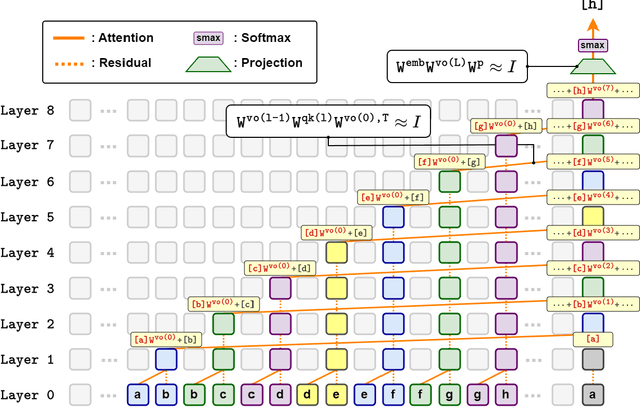
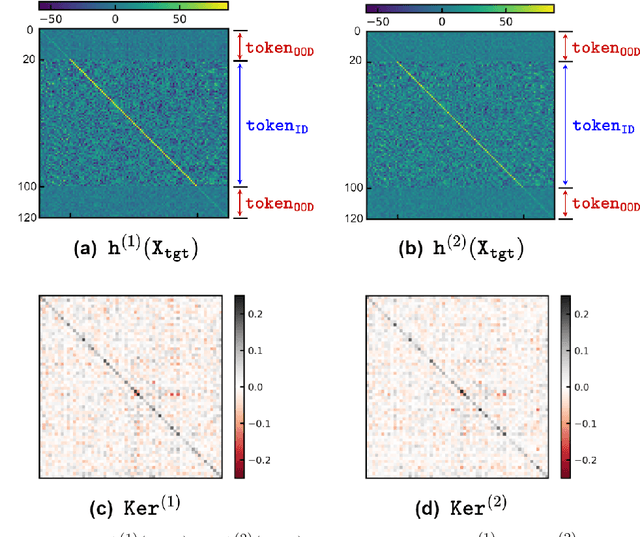
Large language models have consistently struggled with complex reasoning tasks, such as mathematical problem-solving. Investigating the internal reasoning mechanisms of these models can help us design better model architectures and training strategies, ultimately enhancing their reasoning capabilities. In this study, we examine the matching mechanism employed by Transformer for multi-step reasoning on a constructed dataset. We investigate factors that influence the model's matching mechanism and discover that small initialization and post-LayerNorm can facilitate the formation of the matching mechanism, thereby enhancing the model's reasoning ability. Moreover, we propose a method to improve the model's reasoning capability by adding orthogonal noise. Finally, we investigate the parallel reasoning mechanism of Transformers and propose a conjecture on the upper bound of the model's reasoning ability based on this phenomenon. These insights contribute to a deeper understanding of the reasoning processes in large language models and guide designing more effective reasoning architectures and training strategies.

Regularized maximum correntropy machine

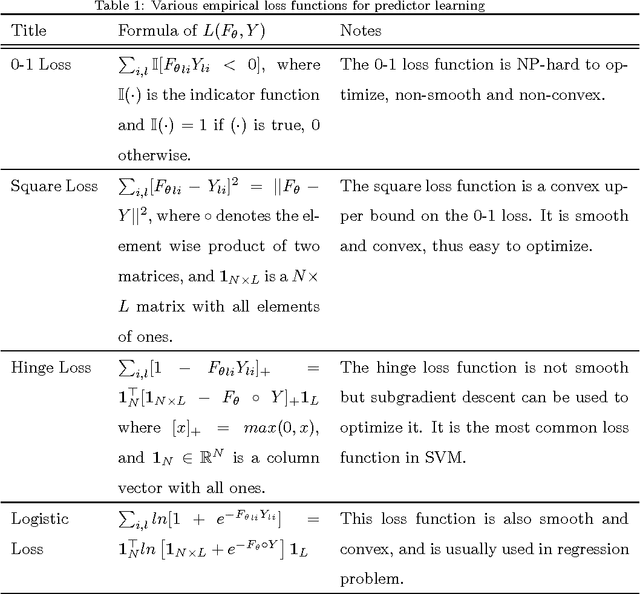
In this paper we investigate the usage of regularized correntropy framework for learning of classifiers from noisy labels. The class label predictors learned by minimizing transitional loss functions are sensitive to the noisy and outlying labels of training samples, because the transitional loss functions are equally applied to all the samples. To solve this problem, we propose to learn the class label predictors by maximizing the correntropy between the predicted labels and the true labels of the training samples, under the regularized Maximum Correntropy Criteria (MCC) framework. Moreover, we regularize the predictor parameter to control the complexity of the predictor. The learning problem is formulated by an objective function considering the parameter regularization and MCC simultaneously. By optimizing the objective function alternately, we develop a novel predictor learning algorithm. The experiments on two chal- lenging pattern classification tasks show that it significantly outperforms the machines with transitional loss functions.