Jim Jing-Yan Wang
Cross-model convolutional neural network for multiple modality data representation
Nov 19, 2016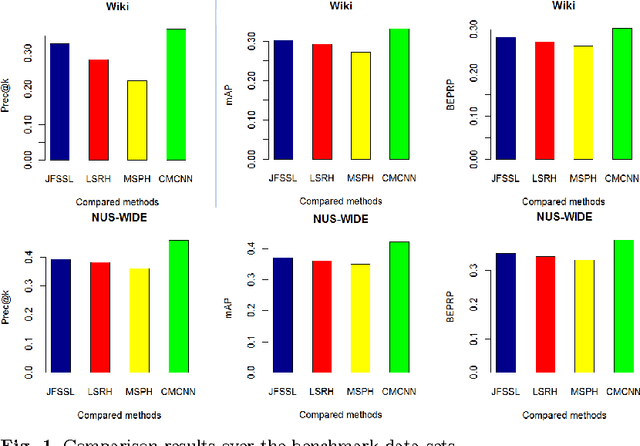
Abstract:A novel data representation method of convolutional neural net- work (CNN) is proposed in this paper to represent data of different modalities. We learn a CNN model for the data of each modality to map the data of differ- ent modalities to a common space, and regularize the new representations in the common space by a cross-model relevance matrix. We further impose that the class label of data points can also be predicted from the CNN representa- tions in the common space. The learning problem is modeled as a minimiza- tion problem, which is solved by an augmented Lagrange method (ALM) with updating rules of Alternating direction method of multipliers (ADMM). The experiments over benchmark of sequence data of multiple modalities show its advantage.
When coding meets ranking: A joint framework based on local learning
Nov 02, 2016



Abstract:Sparse coding, which represents a data point as a sparse reconstruction code with regard to a dictionary, has been a popular data representation method. Meanwhile, in database retrieval problems, learning the ranking scores from data points plays an important role. Up to now, these two problems have always been considered separately, assuming that data coding and ranking are two independent and irrelevant problems. However, is there any internal relationship between sparse coding and ranking score learning? If yes, how to explore and make use of this internal relationship? In this paper, we try to answer these questions by developing the first joint sparse coding and ranking score learning algorithm. To explore the local distribution in the sparse code space, and also to bridge coding and ranking problems, we assume that in the neighborhood of each data point, the ranking scores can be approximated from the corresponding sparse codes by a local linear function. By considering the local approximation error of ranking scores, the reconstruction error and sparsity of sparse coding, and the query information provided by the user, we construct a unified objective function for learning of sparse codes, the dictionary and ranking scores. We further develop an iterative algorithm to solve this optimization problem.
Optimizing Top Precision Performance Measure of Content-Based Image Retrieval by Learning Similarity Function
Aug 20, 2016

Abstract:In this paper we study the problem of content-based image retrieval. In this problem, the most popular performance measure is the top precision measure, and the most important component of a retrieval system is the similarity function used to compare a query image against a database image. However, up to now, there is no existing similarity learning method proposed to optimize the top precision measure. To fill this gap, in this paper, we propose a novel similarity learning method to maximize the top precision measure. We model this problem as a minimization problem with an objective function as the combination of the losses of the relevant images ranked behind the top-ranked irrelevant image, and the squared Frobenius norm of the similarity function parameter. This minimization problem is solved as a quadratic programming problem. The experiments over two benchmark data sets show the advantages of the proposed method over other similarity learning methods when the top precision is used as the performance measure.
A novel transfer learning method based on common space mapping and weighted domain matching
Aug 16, 2016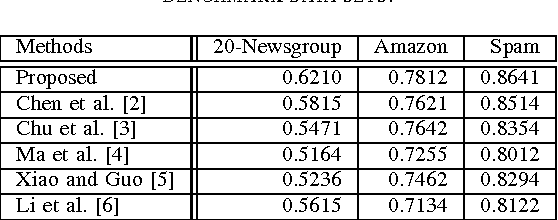
Abstract:In this paper, we propose a novel learning framework for the problem of domain transfer learning. We map the data of two domains to one single common space, and learn a classifier in this common space. Then we adapt the common classifier to the two domains by adding two adaptive functions to it respectively. In the common space, the target domain data points are weighted and matched to the target domain in term of distributions. The weighting terms of source domain data points and the target domain classification responses are also regularized by the local reconstruction coefficients. The novel transfer learning framework is evaluated over some benchmark cross-domain data sets, and it outperforms the existing state-of-the-art transfer learning methods.
Semi-supervised structured output prediction by local linear regression and sub-gradient descent
Aug 16, 2016

Abstract:We propose a novel semi-supervised structured output prediction method based on local linear regression in this paper. The existing semi-supervise structured output prediction methods learn a global predictor for all the data points in a data set, which ignores the differences of local distributions of the data set, and the effects to the structured output prediction. To solve this problem, we propose to learn the missing structured outputs and local predictors for neighborhoods of different data points jointly. Using the local linear regression strategy, in the neighborhood of each data point, we propose to learn a local linear predictor by minimizing both the complexity of the predictor and the upper bound of the structured prediction loss. The minimization problem is solved by sub-gradient descent algorithms. We conduct experiments over two benchmark data sets, and the results show the advantages of the proposed method.
Sparse Coding with Earth Mover's Distance for Multi-Instance Histogram Representation
Mar 14, 2016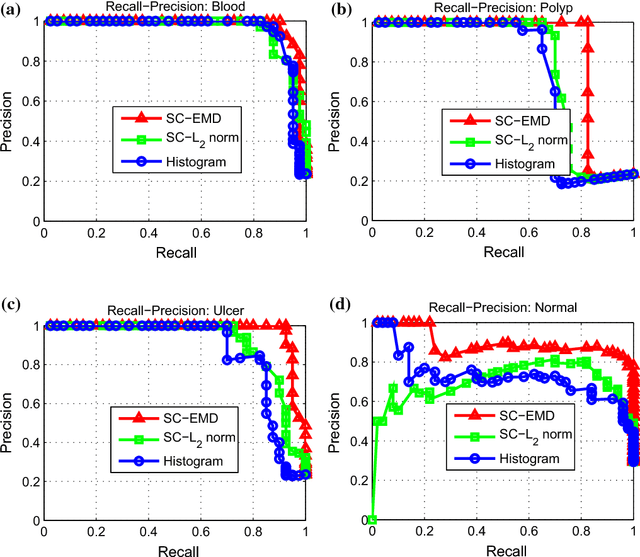
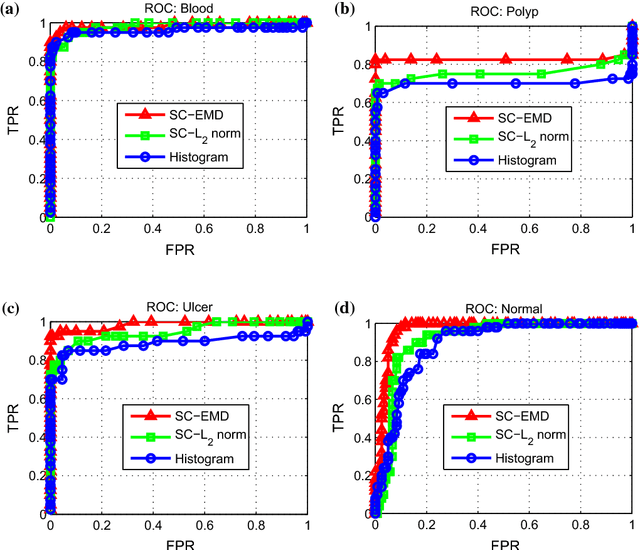
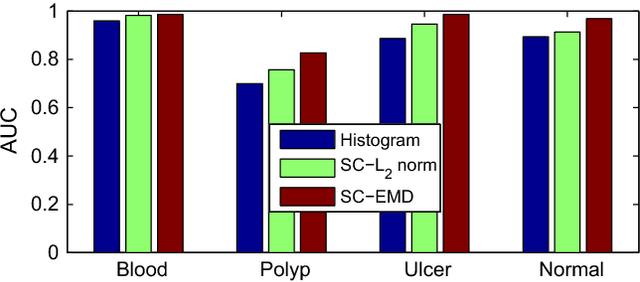
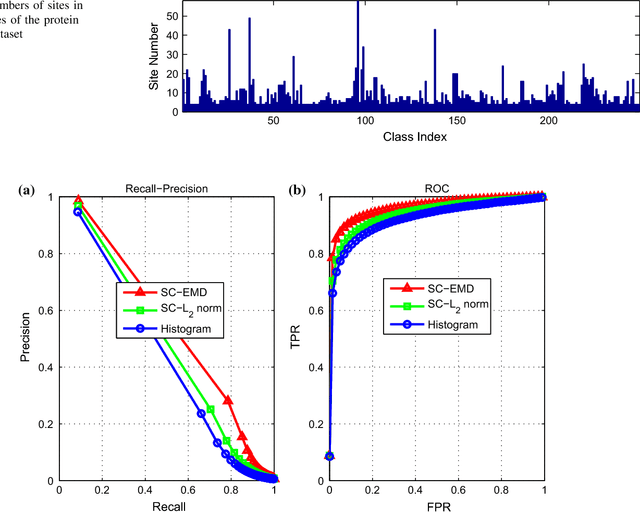
Abstract:Sparse coding (Sc) has been studied very well as a powerful data representation method. It attempts to represent the feature vector of a data sample by reconstructing it as the sparse linear combination of some basic elements, and a $L_2$ norm distance function is usually used as the loss function for the reconstruction error. In this paper, we investigate using Sc as the representation method within multi-instance learning framework, where a sample is given as a bag of instances, and further represented as a histogram of the quantized instances. We argue that for the data type of histogram, using $L_2$ norm distance is not suitable, and propose to use the earth mover's distance (EMD) instead of $L_2$ norm distance as a measure of the reconstruction error. By minimizing the EMD between the histogram of a sample and the its reconstruction from some basic histograms, a novel sparse coding method is developed, which is refereed as SC-EMD. We evaluate its performances as a histogram representation method in tow multi-instance learning problems --- abnormal image detection in wireless capsule endoscopy videos, and protein binding site retrieval. The encouraging results demonstrate the advantages of the new method over the traditional method using $L_2$ norm distance.
Supervised cross-modal factor analysis for multiple modal data classification
Aug 18, 2015

Abstract:In this paper we study the problem of learning from multiple modal data for purpose of document classification. In this problem, each document is composed two different modals of data, i.e., an image and a text. Cross-modal factor analysis (CFA) has been proposed to project the two different modals of data to a shared data space, so that the classification of a image or a text can be performed directly in this space. A disadvantage of CFA is that it has ignored the supervision information. In this paper, we improve CFA by incorporating the supervision information to represent and classify both image and text modals of documents. We project both image and text data to a shared data space by factor analysis, and then train a class label predictor in the shared space to use the class label information. The factor analysis parameter and the predictor parameter are learned jointly by solving one single objective function. With this objective function, we minimize the distance between the projections of image and text of the same document, and the classification error of the projection measured by hinge loss function. The objective function is optimized by an alternate optimization strategy in an iterative algorithm. Experiments in two different multiple modal document data sets show the advantage of the proposed algorithm over other CFA methods.
Regularized maximum correntropy machine
Jan 18, 2015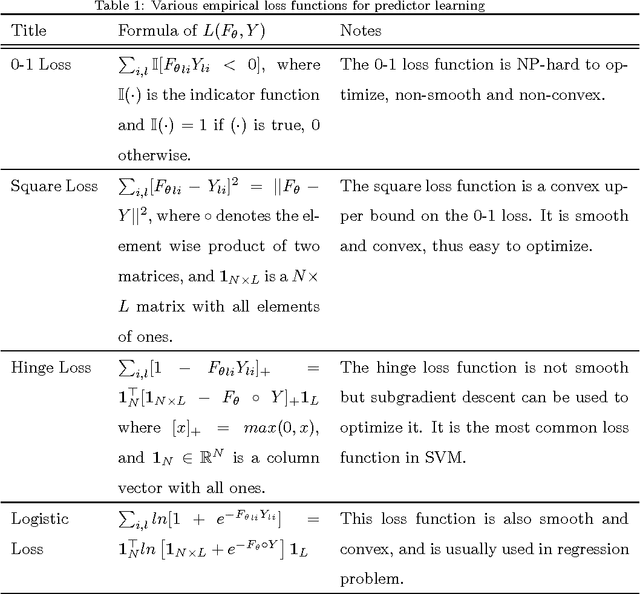



Abstract:In this paper we investigate the usage of regularized correntropy framework for learning of classifiers from noisy labels. The class label predictors learned by minimizing transitional loss functions are sensitive to the noisy and outlying labels of training samples, because the transitional loss functions are equally applied to all the samples. To solve this problem, we propose to learn the class label predictors by maximizing the correntropy between the predicted labels and the true labels of the training samples, under the regularized Maximum Correntropy Criteria (MCC) framework. Moreover, we regularize the predictor parameter to control the complexity of the predictor. The learning problem is formulated by an objective function considering the parameter regularization and MCC simultaneously. By optimizing the objective function alternately, we develop a novel predictor learning algorithm. The experiments on two chal- lenging pattern classification tasks show that it significantly outperforms the machines with transitional loss functions.
Semi-Supervised Sparse Coding
Jan 16, 2015



Abstract:Sparse coding approximates the data sample as a sparse linear combination of some basic codewords and uses the sparse codes as new presentations. In this paper, we investigate learning discriminative sparse codes by sparse coding in a semi-supervised manner, where only a few training samples are labeled. By using the manifold structure spanned by the data set of both labeled and unlabeled samples and the constraints provided by the labels of the labeled samples, we learn the variable class labels for all the samples. Furthermore, to improve the discriminative ability of the learned sparse codes, we assume that the class labels could be predicted from the sparse codes directly using a linear classifier. By solving the codebook, sparse codes, class labels and classifier parameters simultaneously in a unified objective function, we develop a semi-supervised sparse coding algorithm. Experiments on two real-world pattern recognition problems demonstrate the advantage of the proposed methods over supervised sparse coding methods on partially labeled data sets.
Multi-view learning for multivariate performance measures optimization
Jan 16, 2015Abstract:In this paper, we propose the problem of optimizing multivariate performance measures from multi-view data, and an effective method to solve it. This problem has two features: the data points are presented by multiple views, and the target of learning is to optimize complex multivariate performance measures. We propose to learn a linear discriminant functions for each view, and combine them to construct a overall multivariate mapping function for mult-view data. To learn the parameters of the linear dis- criminant functions of different views to optimize multivariate performance measures, we formulate a optimization problem. In this problem, we propose to minimize the complexity of the linear discriminant functions of each view, encourage the consistences of the responses of different views over the same data points, and minimize the upper boundary of a given multivariate performance measure. To optimize this problem, we employ the cutting-plane method in an iterative algorithm. In each iteration, we update a set of constrains, and optimize the mapping function parameter of each view one by one.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge