Zhiwei Bai
Adaptive Preconditioners Trigger Loss Spikes in Adam
Jun 05, 2025Abstract:Loss spikes emerge commonly during training across neural networks of varying architectures and scales when using the Adam optimizer. In this work, we investigate the underlying mechanism responsible for Adam spikes. While previous explanations attribute these phenomena to the lower-loss-as-sharper characteristics of the loss landscape, our analysis reveals that Adam's adaptive preconditioners themselves can trigger spikes. Specifically, we identify a critical regime where squared gradients become substantially smaller than the second-order moment estimates, causing the latter to undergo a $\beta_2$-exponential decay and to respond sluggishly to current gradient information. This mechanism can push the maximum eigenvalue of the preconditioned Hessian beyond the classical stability threshold $2/\eta$ for a sustained period, inducing instability. This instability further leads to an alignment between the gradient and the maximum eigendirection, and a loss spike occurs precisely when the gradient-directional curvature exceeds $2/\eta$. We verify this mechanism through extensive experiments on fully connected networks, convolutional networks, and Transformer architectures.
Scalable Complexity Control Facilitates Reasoning Ability of LLMs
May 29, 2025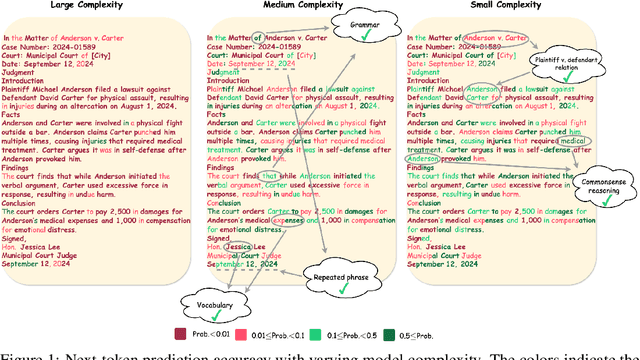
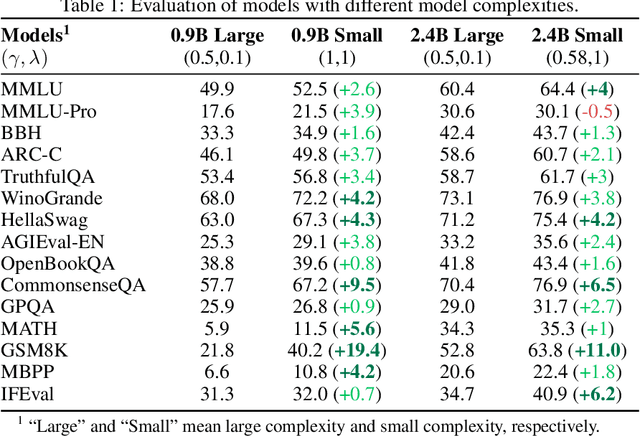
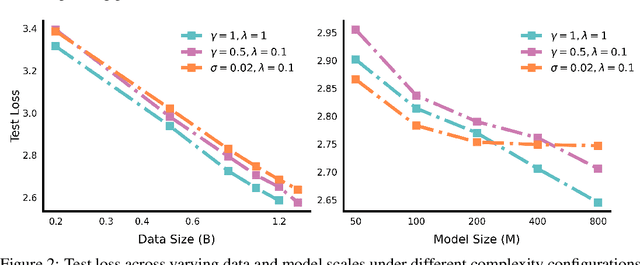
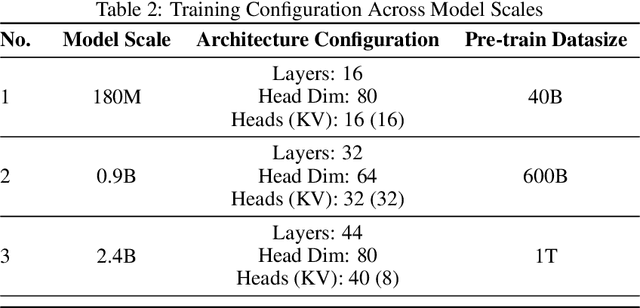
Abstract:The reasoning ability of large language models (LLMs) has been rapidly advancing in recent years, attracting interest in more fundamental approaches that can reliably enhance their generalizability. This work demonstrates that model complexity control, conveniently implementable by adjusting the initialization rate and weight decay coefficient, improves the scaling law of LLMs consistently over varying model sizes and data sizes. This gain is further illustrated by comparing the benchmark performance of 2.4B models pretrained on 1T tokens with different complexity hyperparameters. Instead of fixing the initialization std, we found that a constant initialization rate (the exponent of std) enables the scaling law to descend faster in both model and data sizes. These results indicate that complexity control is a promising direction for the continual advancement of LLMs.
Local Linear Recovery Guarantee of Deep Neural Networks at Overparameterization
Jun 26, 2024
Abstract:Determining whether deep neural network (DNN) models can reliably recover target functions at overparameterization is a critical yet complex issue in the theory of deep learning. To advance understanding in this area, we introduce a concept we term "local linear recovery" (LLR), a weaker form of target function recovery that renders the problem more amenable to theoretical analysis. In the sense of LLR, we prove that functions expressible by narrower DNNs are guaranteed to be recoverable from fewer samples than model parameters. Specifically, we establish upper limits on the optimistic sample sizes, defined as the smallest sample size necessary to guarantee LLR, for functions in the space of a given DNN. Furthermore, we prove that these upper bounds are achieved in the case of two-layer tanh neural networks. Our research lays a solid groundwork for future investigations into the recovery capabilities of DNNs in overparameterized scenarios.
Connectivity Shapes Implicit Regularization in Matrix Factorization Models for Matrix Completion
May 22, 2024



Abstract:Matrix factorization models have been extensively studied as a valuable test-bed for understanding the implicit biases of overparameterized models. Although both low nuclear norm and low rank regularization have been studied for these models, a unified understanding of when, how, and why they achieve different implicit regularization effects remains elusive. In this work, we systematically investigate the implicit regularization of matrix factorization for solving matrix completion problems. We empirically discover that the connectivity of observed data plays a crucial role in the implicit bias, with a transition from low nuclear norm to low rank as data shifts from disconnected to connected with increased observations. We identify a hierarchy of intrinsic invariant manifolds in the loss landscape that guide the training trajectory to evolve from low-rank to higher-rank solutions. Based on this finding, we theoretically characterize the training trajectory as following the hierarchical invariant manifold traversal process, generalizing the characterization of Li et al. (2020) to include the disconnected case. Furthermore, we establish conditions that guarantee minimum nuclear norm, closely aligning with our experimental findings, and we provide a dynamics characterization condition for ensuring minimum rank. Our work reveals the intricate interplay between data connectivity, training dynamics, and implicit regularization in matrix factorization models.
Disentangle Sample Size and Initialization Effect on Perfect Generalization for Single-Neuron Target
May 22, 2024



Abstract:Overparameterized models like deep neural networks have the intriguing ability to recover target functions with fewer sampled data points than parameters (see arXiv:2307.08921). To gain insights into this phenomenon, we concentrate on a single-neuron target recovery scenario, offering a systematic examination of how initialization and sample size influence the performance of two-layer neural networks. Our experiments reveal that a smaller initialization scale is associated with improved generalization, and we identify a critical quantity called the "initial imbalance ratio" that governs training dynamics and generalization under small initialization, supported by theoretical proofs. Additionally, we empirically delineate two critical thresholds in sample size--termed the "optimistic sample size" and the "separation sample size"--that align with the theoretical frameworks established by (see arXiv:2307.08921 and arXiv:2309.00508). Our results indicate a transition in the model's ability to recover the target function: below the optimistic sample size, recovery is unattainable; at the optimistic sample size, recovery becomes attainable albeit with a set of initialization of zero measure. Upon reaching the separation sample size, the set of initialization that can successfully recover the target function shifts from zero to positive measure. These insights, derived from a simplified context, provide a perspective on the intricate yet decipherable complexities of perfect generalization in overparameterized neural networks.
Optimistic Estimate Uncovers the Potential of Nonlinear Models
Jul 18, 2023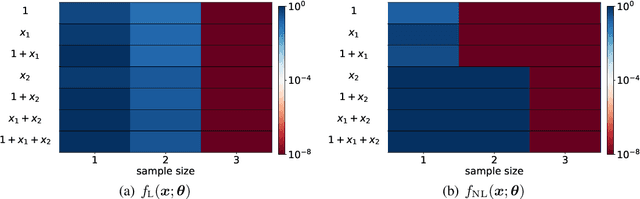
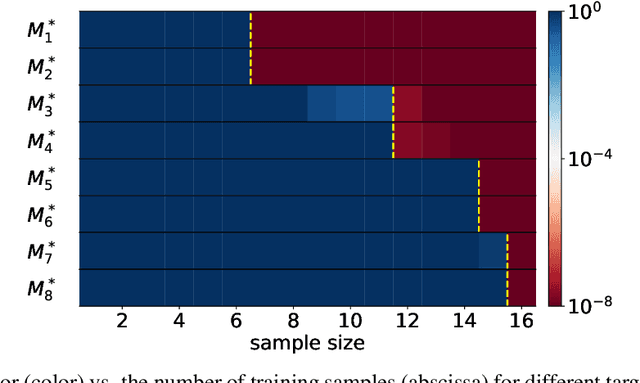
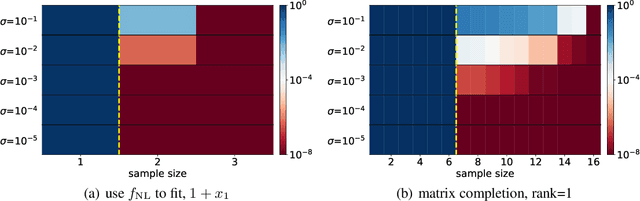
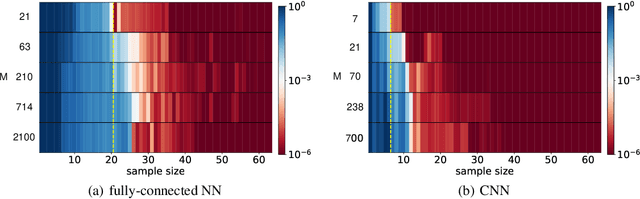
Abstract:We propose an optimistic estimate to evaluate the best possible fitting performance of nonlinear models. It yields an optimistic sample size that quantifies the smallest possible sample size to fit/recover a target function using a nonlinear model. We estimate the optimistic sample sizes for matrix factorization models, deep models, and deep neural networks (DNNs) with fully-connected or convolutional architecture. For each nonlinear model, our estimates predict a specific subset of targets that can be fitted at overparameterization, which are confirmed by our experiments. Our optimistic estimate reveals two special properties of the DNN models -- free expressiveness in width and costly expressiveness in connection. These properties suggest the following architecture design principles of DNNs: (i) feel free to add neurons/kernels; (ii) restrain from connecting neurons. Overall, our optimistic estimate theoretically unveils the vast potential of nonlinear models in fitting at overparameterization. Based on this framework, we anticipate gaining a deeper understanding of how and why numerous nonlinear models such as DNNs can effectively realize their potential in practice in the near future.
Linear Stability Hypothesis and Rank Stratification for Nonlinear Models
Nov 21, 2022



Abstract:Models with nonlinear architectures/parameterizations such as deep neural networks (DNNs) are well known for their mysteriously good generalization performance at overparameterization. In this work, we tackle this mystery from a novel perspective focusing on the transition of the target recovery/fitting accuracy as a function of the training data size. We propose a rank stratification for general nonlinear models to uncover a model rank as an "effective size of parameters" for each function in the function space of the corresponding model. Moreover, we establish a linear stability theory proving that a target function almost surely becomes linearly stable when the training data size equals its model rank. Supported by our experiments, we propose a linear stability hypothesis that linearly stable functions are preferred by nonlinear training. By these results, model rank of a target function predicts a minimal training data size for its successful recovery. Specifically for the matrix factorization model and DNNs of fully-connected or convolutional architectures, our rank stratification shows that the model rank for specific target functions can be much lower than the size of model parameters. This result predicts the target recovery capability even at heavy overparameterization for these nonlinear models as demonstrated quantitatively by our experiments. Overall, our work provides a unified framework with quantitative prediction power to understand the mysterious target recovery behavior at overparameterization for general nonlinear models.
Embedding Principle in Depth for the Loss Landscape Analysis of Deep Neural Networks
May 26, 2022



Abstract:Unraveling the general structure underlying the loss landscapes of deep neural networks (DNNs) is important for the theoretical study of deep learning. Inspired by the embedding principle of DNN loss landscape, we prove in this work an embedding principle in depth that loss landscape of an NN "contains" all critical points of the loss landscapes for shallower NNs. Specifically, we propose a critical lifting operator that any critical point of a shallower network can be lifted to a critical manifold of the target network while preserving the outputs. Through lifting, local minimum of an NN can become a strict saddle point of a deeper NN, which can be easily escaped by first-order methods. The embedding principle in depth reveals a large family of critical points in which layer linearization happens, i.e., computation of certain layers is effectively linear for the training inputs. We empirically demonstrate that, through suppressing layer linearization, batch normalization helps avoid the lifted critical manifolds, resulting in a faster decay of loss. We also demonstrate that increasing training data reduces the lifted critical manifold thus could accelerate the training. Overall, the embedding principle in depth well complements the embedding principle (in width), resulting in a complete characterization of the hierarchical structure of critical points/manifolds of a DNN loss landscape.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge