Adaptive Preconditioners Trigger Loss Spikes in Adam

Loss spikes emerge commonly during training across neural networks of varying architectures and scales when using the Adam optimizer. In this work, we investigate the underlying mechanism responsible for Adam spikes. While previous explanations attribute these phenomena to the lower-loss-as-sharper characteristics of the loss landscape, our analysis reveals that Adam's adaptive preconditioners themselves can trigger spikes. Specifically, we identify a critical regime where squared gradients become substantially smaller than the second-order moment estimates, causing the latter to undergo a $\beta_2$-exponential decay and to respond sluggishly to current gradient information. This mechanism can push the maximum eigenvalue of the preconditioned Hessian beyond the classical stability threshold $2/\eta$ for a sustained period, inducing instability. This instability further leads to an alignment between the gradient and the maximum eigendirection, and a loss spike occurs precisely when the gradient-directional curvature exceeds $2/\eta$. We verify this mechanism through extensive experiments on fully connected networks, convolutional networks, and Transformer architectures.

Scalable Complexity Control Facilitates Reasoning Ability of LLMs

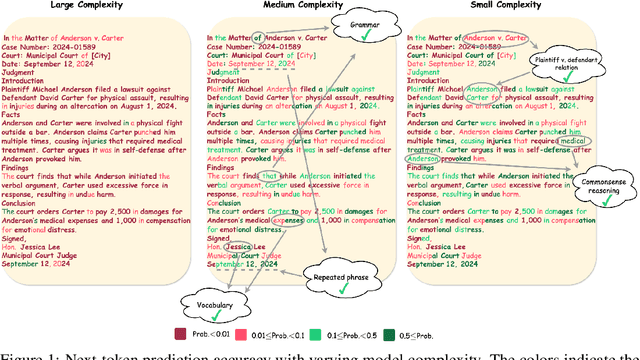
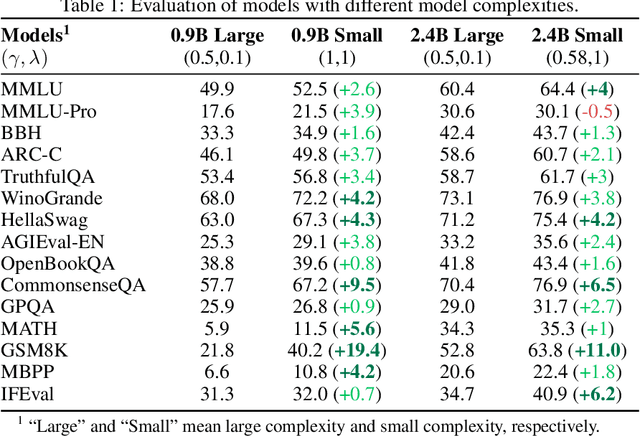
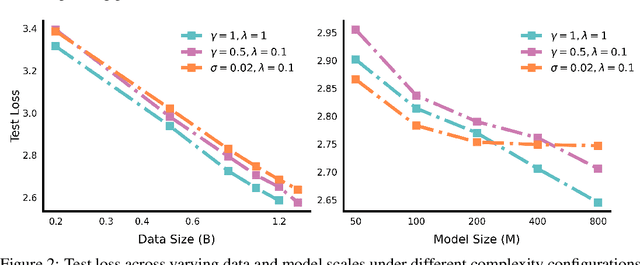
The reasoning ability of large language models (LLMs) has been rapidly advancing in recent years, attracting interest in more fundamental approaches that can reliably enhance their generalizability. This work demonstrates that model complexity control, conveniently implementable by adjusting the initialization rate and weight decay coefficient, improves the scaling law of LLMs consistently over varying model sizes and data sizes. This gain is further illustrated by comparing the benchmark performance of 2.4B models pretrained on 1T tokens with different complexity hyperparameters. Instead of fixing the initialization std, we found that a constant initialization rate (the exponent of std) enables the scaling law to descend faster in both model and data sizes. These results indicate that complexity control is a promising direction for the continual advancement of LLMs.

MemOS: An Operating System for Memory-Augmented Generation (MAG) in Large Language Models

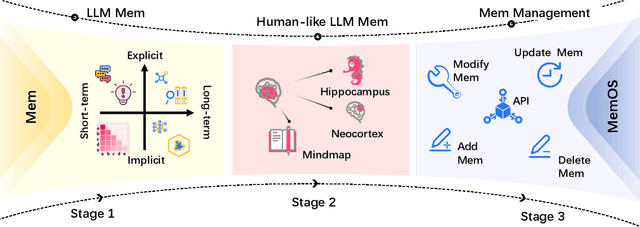
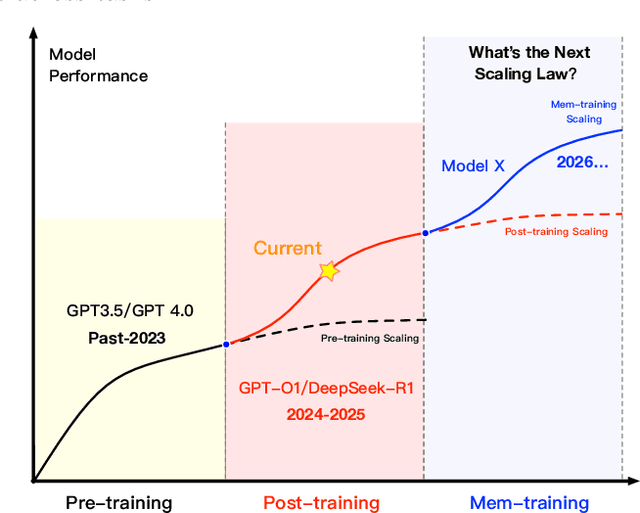
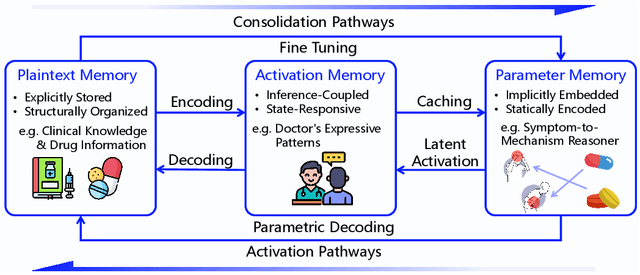
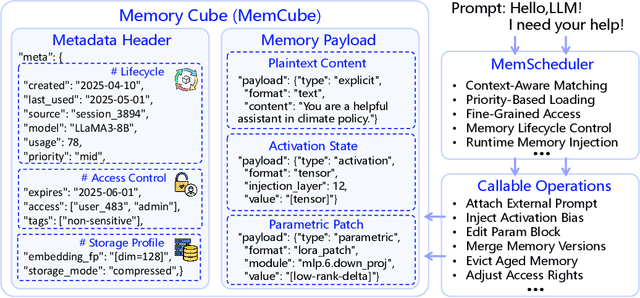
Large Language Models (LLMs) have emerged as foundational infrastructure in the pursuit of Artificial General Intelligence (AGI). Despite their remarkable capabilities in language perception and generation, current LLMs fundamentally lack a unified and structured architecture for handling memory. They primarily rely on parametric memory (knowledge encoded in model weights) and ephemeral activation memory (context-limited runtime states). While emerging methods like Retrieval-Augmented Generation (RAG) incorporate plaintext memory, they lack lifecycle management and multi-modal integration, limiting their capacity for long-term knowledge evolution. To address this, we introduce MemOS, a memory operating system designed for LLMs that, for the first time, elevates memory to a first-class operational resource. It builds unified mechanisms for representation, organization, and governance across three core memory types: parametric, activation, and plaintext. At its core is the MemCube, a standardized memory abstraction that enables tracking, fusion, and migration of heterogeneous memory, while offering structured, traceable access across tasks and contexts. MemOS establishes a memory-centric execution framework with strong controllability, adaptability, and evolvability. It fills a critical gap in current LLM infrastructure and lays the groundwork for continual adaptation, personalized intelligence, and cross-platform coordination in next-generation intelligent systems.

$\text{Memory}^3$: Language Modeling with Explicit Memory

The training and inference of large language models (LLMs) are together a costly process that transports knowledge from raw data to meaningful computation. Inspired by the memory hierarchy of the human brain, we reduce this cost by equipping LLMs with explicit memory, a memory format cheaper than model parameters and text retrieval-augmented generation (RAG). Conceptually, with most of its knowledge externalized to explicit memories, the LLM can enjoy a smaller parameter size, training cost, and inference cost, all proportional to the amount of remaining "abstract knowledge". As a preliminary proof of concept, we train from scratch a 2.4B LLM, which achieves better performance than much larger LLMs as well as RAG models, and maintains higher decoding speed than RAG. The model is named $\text{Memory}^3$, since explicit memory is the third form of memory in LLMs after implicit memory (model parameters) and working memory (context key-values). We introduce a memory circuitry theory to support the externalization of knowledge, and present novel techniques including a memory sparsification mechanism that makes storage tractable and a two-stage pretraining scheme that facilitates memory formation.

A Mathematical Framework for Learning Probability Distributions

The modeling of probability distributions, specifically generative modeling and density estimation, has become an immensely popular subject in recent years by virtue of its outstanding performance on sophisticated data such as images and texts. Nevertheless, a theoretical understanding of its success is still incomplete. One mystery is the paradox between memorization and generalization: In theory, the model is trained to be exactly the same as the empirical distribution of the finite samples, whereas in practice, the trained model can generate new samples or estimate the likelihood of unseen samples. Likewise, the overwhelming diversity of distribution learning models calls for a unified perspective on this subject. This paper provides a mathematical framework such that all the well-known models can be derived based on simple principles. To demonstrate its efficacy, we present a survey of our results on the approximation error, training error and generalization error of these models, which can all be established based on this framework. In particular, the aforementioned paradox is resolved by proving that these models enjoy implicit regularization during training, so that the generalization error at early-stopping avoids the curse of dimensionality. Furthermore, we provide some new results on landscape analysis and the mode collapse phenomenon.

Generalization Error of GAN from the Discriminator's Perspective

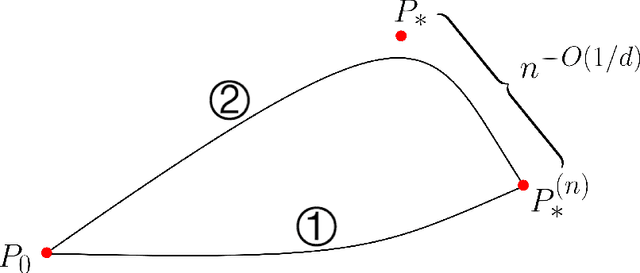
The generative adversarial network (GAN) is a well-known model for learning high-dimensional distributions, but the mechanism for its generalization ability is not understood. In particular, GAN is vulnerable to the memorization phenomenon, the eventual convergence to the empirical distribution. We consider a simplified GAN model with the generator replaced by a density, and analyze how the discriminator contributes to generalization. We show that with early stopping, the generalization error measured by Wasserstein metric escapes from the curse of dimensionality, despite that in the long term, memorization is inevitable. In addition, we present a hardness of learning result for WGAN.

Generalization and Memorization: The Bias Potential Model

Models for learning probability distributions such as generative models and density estimators behave quite differently from models for learning functions. One example is found in the memorization phenomenon, namely the ultimate convergence to the empirical distribution, that occurs in generative adversarial networks (GANs). For this reason, the issue of generalization is more subtle than that for supervised learning. For the bias potential model, we show that dimension-independent generalization accuracy is achievable if early stopping is adopted, despite that in the long term, the model either memorizes the samples or diverges.