Scalable Complexity Control Facilitates Reasoning Ability of LLMs

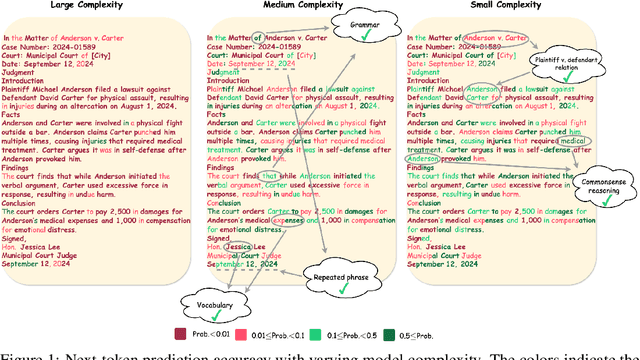
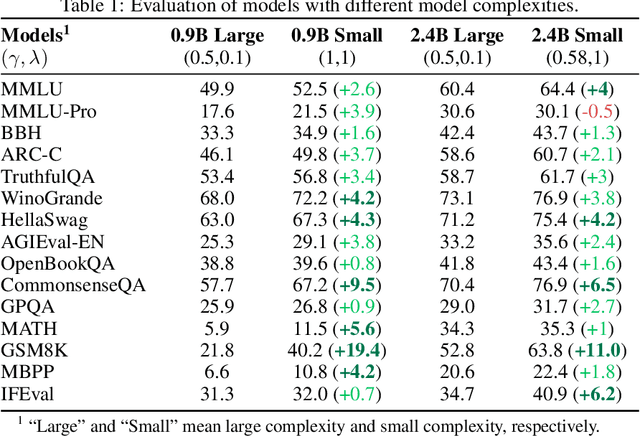
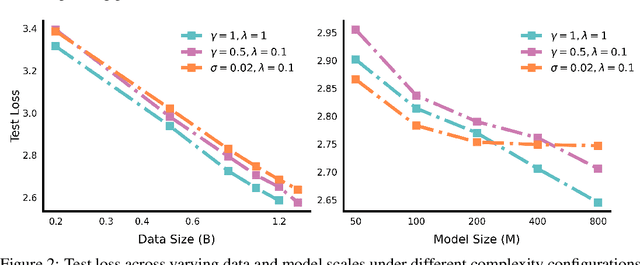
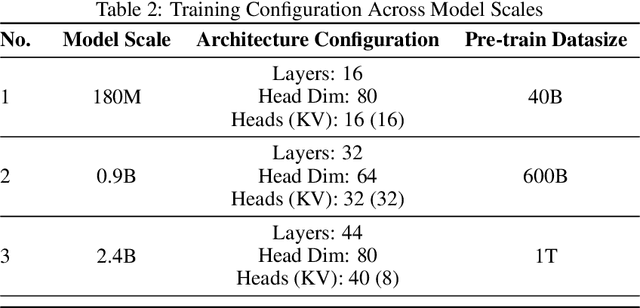
The reasoning ability of large language models (LLMs) has been rapidly advancing in recent years, attracting interest in more fundamental approaches that can reliably enhance their generalizability. This work demonstrates that model complexity control, conveniently implementable by adjusting the initialization rate and weight decay coefficient, improves the scaling law of LLMs consistently over varying model sizes and data sizes. This gain is further illustrated by comparing the benchmark performance of 2.4B models pretrained on 1T tokens with different complexity hyperparameters. Instead of fixing the initialization std, we found that a constant initialization rate (the exponent of std) enables the scaling law to descend faster in both model and data sizes. These results indicate that complexity control is a promising direction for the continual advancement of LLMs.

Reasoning Bias of Next Token Prediction Training

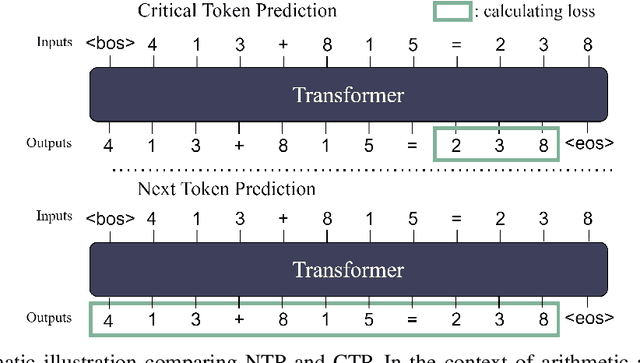
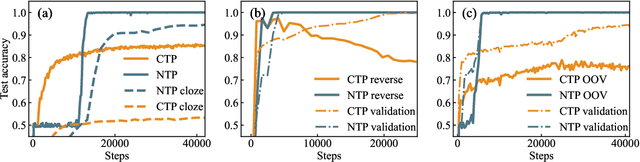
Since the inception of Large Language Models (LLMs), the quest to efficiently train them for superior reasoning capabilities has been a pivotal challenge. The dominant training paradigm for LLMs is based on next token prediction (NTP). Alternative methodologies, called Critical Token Prediction (CTP), focused exclusively on specific critical tokens (such as the answer in Q\&A dataset), aiming to reduce the overfitting of extraneous information and noise. Contrary to initial assumptions, our research reveals that despite NTP's exposure to noise during training, it surpasses CTP in reasoning ability. We attribute this counterintuitive outcome to the regularizing influence of noise on the training dynamics. Our empirical analysis shows that NTP-trained models exhibit enhanced generalization and robustness across various benchmark reasoning datasets, demonstrating greater resilience to perturbations and achieving flatter loss minima. These findings illuminate that NTP is instrumental in fostering reasoning abilities during pretraining, whereas CTP is more effective for finetuning, thereby enriching our comprehension of optimal training strategies in LLM development.

Complexity Control Facilitates Reasoning-Based Compositional Generalization in Transformers

Transformers have demonstrated impressive capabilities across various tasks, yet their performance on compositional problems remains a subject of debate. In this study, we investigate the internal mechanisms underlying Transformers' behavior in compositional tasks. We find that complexity control strategies significantly influence whether the model learns primitive-level rules that generalize out-of-distribution (reasoning-based solutions) or relies solely on memorized mappings (memory-based solutions). By applying masking strategies to the model's information circuits and employing multiple complexity metrics, we reveal distinct internal working mechanisms associated with different solution types. Further analysis reveals that reasoning-based solutions exhibit a lower complexity bias, which aligns with the well-studied neuron condensation phenomenon. This lower complexity bias is hypothesized to be the key factor enabling these solutions to learn reasoning rules. We validate these conclusions across multiple real-world datasets, including image generation and natural language processing tasks, confirming the broad applicability of our findings.

Initialization is Critical to Whether Transformers Fit Composite Functions by Inference or Memorizing

Transformers have shown impressive capabilities across various tasks, but their performance on compositional problems remains a topic of debate. In this work, we investigate the mechanisms of how transformers behave on unseen compositional tasks using anchor functions. We discover that the parameter initialization scale plays a critical role in determining whether the model learns inferential solutions, which capture the underlying compositional primitives, or symmetric solutions, which simply memorize mappings without understanding the compositional structure. By analyzing the information flow and vector representations within the model, we reveal the distinct mechanisms underlying these solution types. We further find that inferential solutions exhibit low complexity bias, which we hypothesize is a key factor enabling them to learn individual mappings for single anchors. Building upon our understanding of these mechanisms, we can predict the learning behavior of models with different initialization scales when faced with data of varying inferential complexity. Our findings provide valuable insights into the role of initialization scale in shaping the type of solution learned by transformers and their ability to learn and generalize compositional functions.