Uncovering Critical Sets of Deep Neural Networks via Sample-Independent Critical Lifting

This paper investigates the sample dependence of critical points for neural networks. We introduce a sample-independent critical lifting operator that associates a parameter of one network with a set of parameters of another, thus defining sample-dependent and sample-independent lifted critical points. We then show by example that previously studied critical embeddings do not capture all sample-independent lifted critical points. Finally, we demonstrate the existence of sample-dependent lifted critical points for sufficiently large sample sizes and prove that saddles appear among them.

Local Linear Recovery Guarantee of Deep Neural Networks at Overparameterization

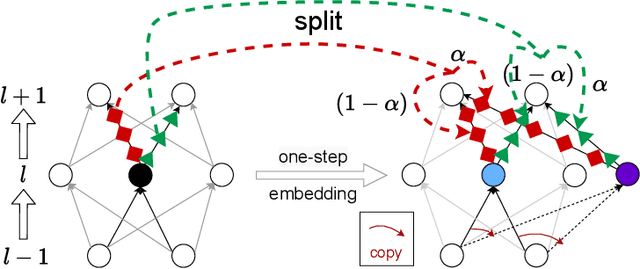
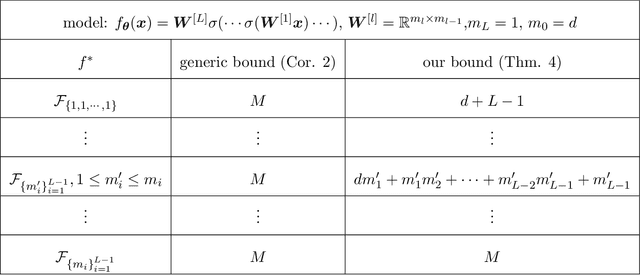
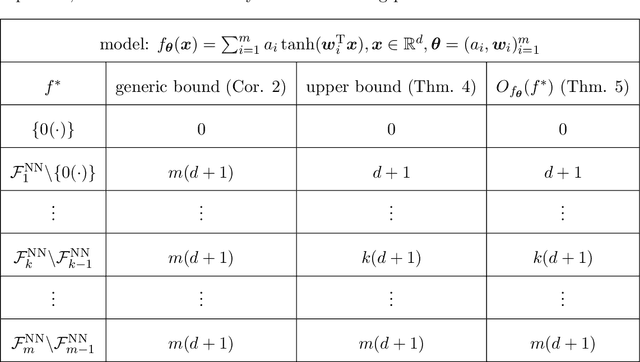
Determining whether deep neural network (DNN) models can reliably recover target functions at overparameterization is a critical yet complex issue in the theory of deep learning. To advance understanding in this area, we introduce a concept we term "local linear recovery" (LLR), a weaker form of target function recovery that renders the problem more amenable to theoretical analysis. In the sense of LLR, we prove that functions expressible by narrower DNNs are guaranteed to be recoverable from fewer samples than model parameters. Specifically, we establish upper limits on the optimistic sample sizes, defined as the smallest sample size necessary to guarantee LLR, for functions in the space of a given DNN. Furthermore, we prove that these upper bounds are achieved in the case of two-layer tanh neural networks. Our research lays a solid groundwork for future investigations into the recovery capabilities of DNNs in overparameterized scenarios.

Geometry of Critical Sets and Existence of Saddle Branches for Two-layer Neural Networks

This paper presents a comprehensive analysis of critical point sets in two-layer neural networks. To study such complex entities, we introduce the critical embedding operator and critical reduction operator as our tools. Given a critical point, we use these operators to uncover the whole underlying critical set representing the same output function, which exhibits a hierarchical structure. Furthermore, we prove existence of saddle branches for any critical set whose output function can be represented by a narrower network. Our results provide a solid foundation to the further study of optimization and training behavior of neural networks.

Structure and Gradient Dynamics Near Global Minima of Two-layer Neural Networks

Under mild assumptions, we investigate the structure of loss landscape of two-layer neural networks near global minima, determine the set of parameters which give perfect generalization, and fully characterize the gradient flows around it. With novel techniques, our work uncovers some simple aspects of the complicated loss landscape and reveals how model, target function, samples and initialization affect the training dynamics differently. Based on these results, we also explain why (overparametrized) neural networks could generalize well.

Optimistic Estimate Uncovers the Potential of Nonlinear Models

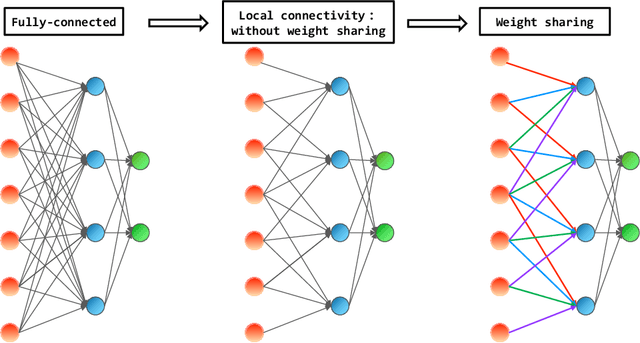
We propose an optimistic estimate to evaluate the best possible fitting performance of nonlinear models. It yields an optimistic sample size that quantifies the smallest possible sample size to fit/recover a target function using a nonlinear model. We estimate the optimistic sample sizes for matrix factorization models, deep models, and deep neural networks (DNNs) with fully-connected or convolutional architecture. For each nonlinear model, our estimates predict a specific subset of targets that can be fitted at overparameterization, which are confirmed by our experiments. Our optimistic estimate reveals two special properties of the DNN models -- free expressiveness in width and costly expressiveness in connection. These properties suggest the following architecture design principles of DNNs: (i) feel free to add neurons/kernels; (ii) restrain from connecting neurons. Overall, our optimistic estimate theoretically unveils the vast potential of nonlinear models in fitting at overparameterization. Based on this framework, we anticipate gaining a deeper understanding of how and why numerous nonlinear models such as DNNs can effectively realize their potential in practice in the near future.

Linear Stability Hypothesis and Rank Stratification for Nonlinear Models

Models with nonlinear architectures/parameterizations such as deep neural networks (DNNs) are well known for their mysteriously good generalization performance at overparameterization. In this work, we tackle this mystery from a novel perspective focusing on the transition of the target recovery/fitting accuracy as a function of the training data size. We propose a rank stratification for general nonlinear models to uncover a model rank as an "effective size of parameters" for each function in the function space of the corresponding model. Moreover, we establish a linear stability theory proving that a target function almost surely becomes linearly stable when the training data size equals its model rank. Supported by our experiments, we propose a linear stability hypothesis that linearly stable functions are preferred by nonlinear training. By these results, model rank of a target function predicts a minimal training data size for its successful recovery. Specifically for the matrix factorization model and DNNs of fully-connected or convolutional architectures, our rank stratification shows that the model rank for specific target functions can be much lower than the size of model parameters. This result predicts the target recovery capability even at heavy overparameterization for these nonlinear models as demonstrated quantitatively by our experiments. Overall, our work provides a unified framework with quantitative prediction power to understand the mysterious target recovery behavior at overparameterization for general nonlinear models.

Limitation of characterizing implicit regularization by data-independent functions

In recent years, understanding the implicit regularization of neural networks (NNs) has become a central task of deep learning theory. However, implicit regularization is in itself not completely defined and well understood. In this work, we make an attempt to mathematically define and study the implicit regularization. Importantly, we explore the limitation of a common approach of characterizing the implicit regularization by data-independent functions. We propose two dynamical mechanisms, i.e., Two-point and One-point Overlapping mechanisms, based on which we provide two recipes for producing classes of one-hidden-neuron NNs that provably cannot be fully characterized by a type of or all data-independent functions. Our results signify the profound data-dependency of implicit regularization in general, inspiring us to study in detail the data-dependency of NN implicit regularization in the future.