Understanding and Mitigating the High Computational Cost in Path Data Diffusion

Advancements in mobility services, navigation systems, and smart transportation technologies have made it possible to collect large amounts of path data. Modeling the distribution of this path data, known as the Path Generation (PG) problem, is crucial for understanding urban mobility patterns and developing intelligent transportation systems. Recent studies have explored using diffusion models to address the PG problem due to their ability to capture multimodal distributions and support conditional generation. A recent work devises a diffusion process explicitly in graph space and achieves state-of-the-art performance. However, this method suffers a high computation cost in terms of both time and memory, which prohibits its application. In this paper, we analyze this method both theoretically and experimentally and find that the main culprit of its high computation cost is its explicit design of the diffusion process in graph space. To improve efficiency, we devise a Latent-space Path Diffusion (LPD) model, which operates in latent space instead of graph space. Our LPD significantly reduces both time and memory costs by up to 82.8% and 83.1%, respectively. Despite these reductions, our approach does not suffer from performance degradation. It outperforms the state-of-the-art method in most scenarios by 24.5%~34.0%.

Loss Jump During Loss Switch in Solving PDEs with Neural Networks

Using neural networks to solve partial differential equations (PDEs) is gaining popularity as an alternative approach in the scientific computing community. Neural networks can integrate different types of information into the loss function. These include observation data, governing equations, and variational forms, etc. These loss functions can be broadly categorized into two types: observation data loss directly constrains and measures the model output, while other loss functions indirectly model the performance of the network, which can be classified as model loss. However, this alternative approach lacks a thorough understanding of its underlying mechanisms, including theoretical foundations and rigorous characterization of various phenomena. This work focuses on investigating how different loss functions impact the training of neural networks for solving PDEs. We discover a stable loss-jump phenomenon: when switching the loss function from the data loss to the model loss, which includes different orders of derivative information, the neural network solution significantly deviates from the exact solution immediately. Further experiments reveal that this phenomenon arises from the different frequency preferences of neural networks under different loss functions. We theoretically analyze the frequency preference of neural networks under model loss. This loss-jump phenomenon provides a valuable perspective for examining the underlying mechanisms of neural networks in solving PDEs.

Data-informed Deep Optimization

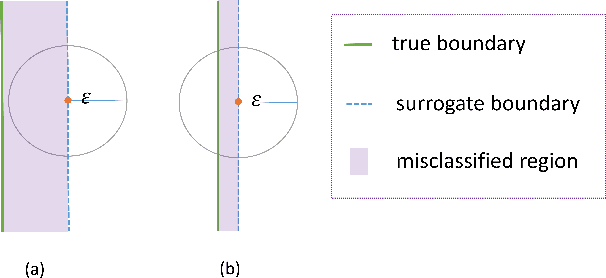
Complex design problems are common in the scientific and industrial fields. In practice, objective functions or constraints of these problems often do not have explicit formulas, and can be estimated only at a set of sampling points through experiments or simulations. Such optimization problems are especially challenging when design parameters are high-dimensional due to the curse of dimensionality. In this work, we propose a data-informed deep optimization (DiDo) approach as follows: first, we use a deep neural network (DNN) classifier to learn the feasible region; second, we sample feasible points based on the DNN classifier for fitting of the objective function; finally, we find optimal points of the DNN-surrogate optimization problem by gradient descent. To demonstrate the effectiveness of our DiDo approach, we consider a practical design case in industry, in which our approach yields good solutions using limited size of training data. We further use a 100-dimension toy example to show the effectiveness of our model for higher dimensional problems. Our results indicate that the DiDo approach empowered by DNN is flexible and promising for solving general high-dimensional design problems in practice.

MOD-Net: A Machine Learning Approach via Model-Operator-Data Network for Solving PDEs

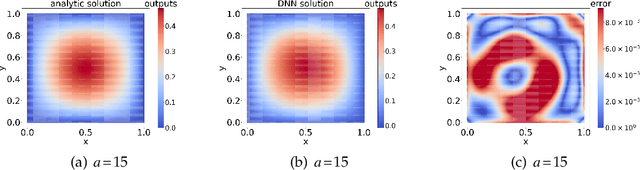
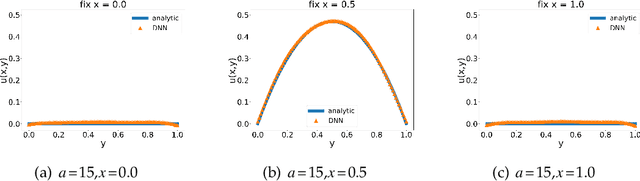
In this paper, we propose a model-operator-data network (MOD-Net) for solving PDEs. A MOD-Net is driven by a model to solve PDEs based on operator representation with regularization from data. In this work, we use a deep neural network to parameterize the Green's function. The empirical risk consists of the mean square of the governing equation, boundary conditions, and a few labels, which are numerically computed by traditional schemes on coarse grid points with cheap computation cost. With only the labeled dataset or only the model constraints, it is insufficient to accurately train a MOD-Net for complicate problems. Intuitively, the labeled dataset works as a regularization in addition to the model constraints. The MOD-Net is much efficient than original neural operator because the MOD-Net also uses the information of governing equation and the boundary conditions of the PDE rather than purely the expensive labels. Since the MOD-Net learns the Green's function of a PDE, it solves a type of PDEs but not a specific case. We numerically show MOD-Net is very efficient in solving Poisson equation and one-dimensional Boltzmann equation. For non-linear PDEs, where the concept of the Green's function does not apply, the non-linear MOD-Net can be similarly used as an ansatz for solving non-linear PDEs.

Predicting Individual Treatment Effects of Large-scale Team Competitions in a Ride-sharing Economy

Millions of drivers worldwide have enjoyed financial benefits and work schedule flexibility through a ride-sharing economy, but meanwhile they have suffered from the lack of a sense of identity and career achievement. Equipped with social identity and contest theories, financially incentivized team competitions have been an effective instrument to increase drivers' productivity, job satisfaction, and retention, and to improve revenue over cost for ride-sharing platforms. While these competitions are overall effective, the decisive factors behind the treatment effects and how they affect the outcomes of individual drivers have been largely mysterious. In this study, we analyze data collected from more than 500 large-scale team competitions organized by a leading ride-sharing platform, building machine learning models to predict individual treatment effects. Through a careful investigation of features and predictors, we are able to reduce out-sample prediction error by more than 24%. Through interpreting the best-performing models, we discover many novel and actionable insights regarding how to optimize the design and the execution of team competitions on ride-sharing platforms. A simulated analysis demonstrates that by simply changing a few contest design options, the average treatment effect of a real competition is expected to increase by as much as 26%. Our procedure and findings shed light on how to analyze and optimize large-scale online field experiments in general.