Breaking the $\log(1/Δ_2)$ Barrier: Better Batched Best Arm Identification with Adaptive Grids

We investigate the problem of batched best arm identification in multi-armed bandits, where we aim to identify the best arm from a set of $n$ arms while minimizing both the number of samples and batches. We introduce an algorithm that achieves near-optimal sample complexity and features an instance-sensitive batch complexity, which breaks the $\log(1/\Delta_2)$ barrier. The main contribution of our algorithm is a novel sample allocation scheme that effectively balances exploration and exploitation for batch sizes. Experimental results indicate that our approach is more batch-efficient across various setups. We also extend this framework to the problem of batched best arm identification in linear bandits and achieve similar improvements.

Optimal Streaming Algorithms for Multi-Armed Bandits

This paper studies two variants of the best arm identification (BAI) problem under the streaming model, where we have a stream of $n$ arms with reward distributions supported on $[0,1]$ with unknown means. The arms in the stream are arriving one by one, and the algorithm cannot access an arm unless it is stored in a limited size memory. We first study the streaming \eps-$top$-$k$ arms identification problem, which asks for $k$ arms whose reward means are lower than that of the $k$-th best arm by at most $\eps$ with probability at least $1-\delta$. For general $\eps \in (0,1)$, the existing solution for this problem assumes $k = 1$ and achieves the optimal sample complexity $O(\frac{n}{\eps^2} \log \frac{1}{\delta})$ using $O(\log^*(n))$ ($\log^*(n)$ equals the number of times that we need to apply the logarithm function on $n$ before the results is no more than 1.) memory and a single pass of the stream. We propose an algorithm that works for any $k$ and achieves the optimal sample complexity $O(\frac{n}{\eps^2} \log\frac{k}{\delta})$ using a single-arm memory and a single pass of the stream. Second, we study the streaming BAI problem, where the objective is to identify the arm with the maximum reward mean with at least $1-\delta$ probability, using a single-arm memory and as few passes of the input stream as possible. We present a single-arm-memory algorithm that achieves a near instance-dependent optimal sample complexity within $O(\log \Delta_2^{-1})$ passes, where $\Delta_2$ is the gap between the mean of the best arm and that of the second best arm.

Best Arm Identification with Minimal Regret

Motivated by real-world applications that necessitate responsible experimentation, we introduce the problem of best arm identification (BAI) with minimal regret. This innovative variant of the multi-armed bandit problem elegantly amalgamates two of its most ubiquitous objectives: regret minimization and BAI. More precisely, the agent's goal is to identify the best arm with a prescribed confidence level $\delta$, while minimizing the cumulative regret up to the stopping time. Focusing on single-parameter exponential families of distributions, we leverage information-theoretic techniques to establish an instance-dependent lower bound on the expected cumulative regret. Moreover, we present an intriguing impossibility result that underscores the tension between cumulative regret and sample complexity in fixed-confidence BAI. Complementarily, we design and analyze the Double KL-UCB algorithm, which achieves asymptotic optimality as the confidence level tends to zero. Notably, this algorithm employs two distinct confidence bounds to guide arm selection in a randomized manner. Our findings elucidate a fresh perspective on the inherent connections between regret minimization and BAI.

Optimal Batched Linear Bandits

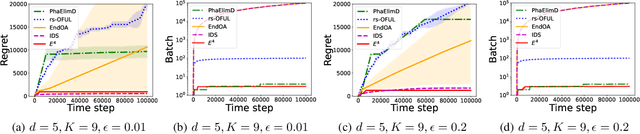
We introduce the E$^4$ algorithm for the batched linear bandit problem, incorporating an Explore-Estimate-Eliminate-Exploit framework. With a proper choice of exploration rate, we prove E$^4$ achieves the finite-time minimax optimal regret with only $O(\log\log T)$ batches, and the asymptotically optimal regret with only $3$ batches as $T\rightarrow\infty$, where $T$ is the time horizon. We further prove a lower bound on the batch complexity of linear contextual bandits showing that any asymptotically optimal algorithm must require at least $3$ batches in expectation as $T\rightarrow\infty$, which indicates E$^4$ achieves the asymptotic optimality in regret and batch complexity simultaneously. To the best of our knowledge, E$^4$ is the first algorithm for linear bandits that simultaneously achieves the minimax and asymptotic optimality in regret with the corresponding optimal batch complexities. In addition, we show that with another choice of exploration rate E$^4$ achieves an instance-dependent regret bound requiring at most $O(\log T)$ batches, and maintains the minimax optimality and asymptotic optimality. We conduct thorough experiments to evaluate our algorithm on randomly generated instances and the challenging \textit{End of Optimism} instances \citep{lattimore2017end} which were shown to be hard to learn for optimism based algorithms. Empirical results show that E$^4$ consistently outperforms baseline algorithms with respect to regret minimization, batch complexity, and computational efficiency.

Sparsity-Agnostic Linear Bandits with Adaptive Adversaries

We study stochastic linear bandits where, in each round, the learner receives a set of actions (i.e., feature vectors), from which it chooses an element and obtains a stochastic reward. The expected reward is a fixed but unknown linear function of the chosen action. We study sparse regret bounds, that depend on the number $S$ of non-zero coefficients in the linear reward function. Previous works focused on the case where $S$ is known, or the action sets satisfy additional assumptions. In this work, we obtain the first sparse regret bounds that hold when $S$ is unknown and the action sets are adversarially generated. Our techniques combine online to confidence set conversions with a novel randomized model selection approach over a hierarchy of nested confidence sets. When $S$ is known, our analysis recovers state-of-the-art bounds for adversarial action sets. We also show that a variant of our approach, using Exp3 to dynamically select the confidence sets, can be used to improve the empirical performance of stochastic linear bandits while enjoying a regret bound with optimal dependence on the time horizon.

Multi-Armed Bandits with Abstention

We introduce a novel extension of the canonical multi-armed bandit problem that incorporates an additional strategic element: abstention. In this enhanced framework, the agent is not only tasked with selecting an arm at each time step, but also has the option to abstain from accepting the stochastic instantaneous reward before observing it. When opting for abstention, the agent either suffers a fixed regret or gains a guaranteed reward. Given this added layer of complexity, we ask whether we can develop efficient algorithms that are both asymptotically and minimax optimal. We answer this question affirmatively by designing and analyzing algorithms whose regrets meet their corresponding information-theoretic lower bounds. Our results offer valuable quantitative insights into the benefits of the abstention option, laying the groundwork for further exploration in other online decision-making problems with such an option. Numerical results further corroborate our theoretical findings.

Finite-Time Frequentist Regret Bounds of Multi-Agent Thompson Sampling on Sparse Hypergraphs

We study the multi-agent multi-armed bandit (MAMAB) problem, where $m$ agents are factored into $\rho$ overlapping groups. Each group represents a hyperedge, forming a hypergraph over the agents. At each round of interaction, the learner pulls a joint arm (composed of individual arms for each agent) and receives a reward according to the hypergraph structure. Specifically, we assume there is a local reward for each hyperedge, and the reward of the joint arm is the sum of these local rewards. Previous work introduced the multi-agent Thompson sampling (MATS) algorithm \citep{verstraeten2020multiagent} and derived a Bayesian regret bound. However, it remains an open problem how to derive a frequentist regret bound for Thompson sampling in this multi-agent setting. To address these issues, we propose an efficient variant of MATS, the $\epsilon$-exploring Multi-Agent Thompson Sampling ($\epsilon$-MATS) algorithm, which performs MATS exploration with probability $\epsilon$ while adopts a greedy policy otherwise. We prove that $\epsilon$-MATS achieves a worst-case frequentist regret bound that is sublinear in both the time horizon and the local arm size. We also derive a lower bound for this setting, which implies our frequentist regret upper bound is optimal up to constant and logarithm terms, when the hypergraph is sufficiently sparse. Thorough experiments on standard MAMAB problems demonstrate the superior performance and the improved computational efficiency of $\epsilon$-MATS compared with existing algorithms in the same setting.

Optimal Batched Best Arm Identification

We study the batched best arm identification (BBAI) problem, where the learner's goal is to identify the best arm while switching the policy as less as possible. In particular, we aim to find the best arm with probability $1-\delta$ for some small constant $\delta>0$ while minimizing both the sample complexity (total number of arm pulls) and the batch complexity (total number of batches). We propose the three-batch best arm identification (Tri-BBAI) algorithm, which is the first batched algorithm that achieves the optimal sample complexity in the asymptotic setting (i.e., $\delta\rightarrow 0$) and runs only in at most $3$ batches. Based on Tri-BBAI, we further propose the almost optimal batched best arm identification (Opt-BBAI) algorithm, which is the first algorithm that achieves the near-optimal sample and batch complexity in the non-asymptotic setting (i.e., $\delta>0$ is arbitrarily fixed), while enjoying the same batch and sample complexity as Tri-BBAI when $\delta$ tends to zero. Moreover, in the non-asymptotic setting, the complexity of previous batch algorithms is usually conditioned on the event that the best arm is returned (with a probability of at least $1-\delta$), which is potentially unbounded in cases where a sub-optimal arm is returned. In contrast, the complexity of Opt-BBAI does not rely on such an event. This is achieved through a novel procedure that we design for checking whether the best arm is eliminated, which is of independent interest.

Finite-Time Regret of Thompson Sampling Algorithms for Exponential Family Multi-Armed Bandits

We study the regret of Thompson sampling (TS) algorithms for exponential family bandits, where the reward distribution is from a one-dimensional exponential family, which covers many common reward distributions including Bernoulli, Gaussian, Gamma, Exponential, etc. We propose a Thompson sampling algorithm, termed ExpTS, which uses a novel sampling distribution to avoid the under-estimation of the optimal arm. We provide a tight regret analysis for ExpTS, which simultaneously yields both the finite-time regret bound as well as the asymptotic regret bound. In particular, for a $K$-armed bandit with exponential family rewards, ExpTS over a horizon $T$ is sub-UCB (a strong criterion for the finite-time regret that is problem-dependent), minimax optimal up to a factor $\sqrt{\log K}$, and asymptotically optimal, for exponential family rewards. Moreover, we propose ExpTS$^+$, by adding a greedy exploitation step in addition to the sampling distribution used in ExpTS, to avoid the over-estimation of sub-optimal arms. ExpTS$^+$ is an anytime bandit algorithm and achieves the minimax optimality and asymptotic optimality simultaneously for exponential family reward distributions. Our proof techniques are general and conceptually simple and can be easily applied to analyze standard Thompson sampling with specific reward distributions.

MOTS: Minimax Optimal Thompson Sampling

Thompson sampling is one of the most widely used algorithms for many online decision problems, due to its simplicity in implementation and superior empirical performance over other state-of-the-art methods. Despite its popularity and empirical success, it has remained an open problem whether Thompson sampling can achieve the minimax optimal regret $O(\sqrt{KT})$ for $K$-armed bandit problems, where $T$ is the total time horizon. In this paper, we solve this long open problem by proposing a new Thompson sampling algorithm called MOTS that adaptively truncates the sampling result of the chosen arm at each time step. We prove that this simple variant of Thompson sampling achieves the minimax optimal regret bound $O(\sqrt{KT})$ for finite time horizon $T$ and also the asymptotic optimal regret bound when $T$ grows to infinity as well. This is the first time that the minimax optimality of multi-armed bandit problems has been attained by Thompson sampling type of algorithms.