Best Arm Identification with Minimal Regret

Motivated by real-world applications that necessitate responsible experimentation, we introduce the problem of best arm identification (BAI) with minimal regret. This innovative variant of the multi-armed bandit problem elegantly amalgamates two of its most ubiquitous objectives: regret minimization and BAI. More precisely, the agent's goal is to identify the best arm with a prescribed confidence level $\delta$, while minimizing the cumulative regret up to the stopping time. Focusing on single-parameter exponential families of distributions, we leverage information-theoretic techniques to establish an instance-dependent lower bound on the expected cumulative regret. Moreover, we present an intriguing impossibility result that underscores the tension between cumulative regret and sample complexity in fixed-confidence BAI. Complementarily, we design and analyze the Double KL-UCB algorithm, which achieves asymptotic optimality as the confidence level tends to zero. Notably, this algorithm employs two distinct confidence bounds to guide arm selection in a randomized manner. Our findings elucidate a fresh perspective on the inherent connections between regret minimization and BAI.

Multi-Armed Bandits with Abstention

We introduce a novel extension of the canonical multi-armed bandit problem that incorporates an additional strategic element: abstention. In this enhanced framework, the agent is not only tasked with selecting an arm at each time step, but also has the option to abstain from accepting the stochastic instantaneous reward before observing it. When opting for abstention, the agent either suffers a fixed regret or gains a guaranteed reward. Given this added layer of complexity, we ask whether we can develop efficient algorithms that are both asymptotically and minimax optimal. We answer this question affirmatively by designing and analyzing algorithms whose regrets meet their corresponding information-theoretic lower bounds. Our results offer valuable quantitative insights into the benefits of the abstention option, laying the groundwork for further exploration in other online decision-making problems with such an option. Numerical results further corroborate our theoretical findings.

Block-Level MU-MISO Interference Exploitation Precoding: Optimal Structure and Explicit Duality

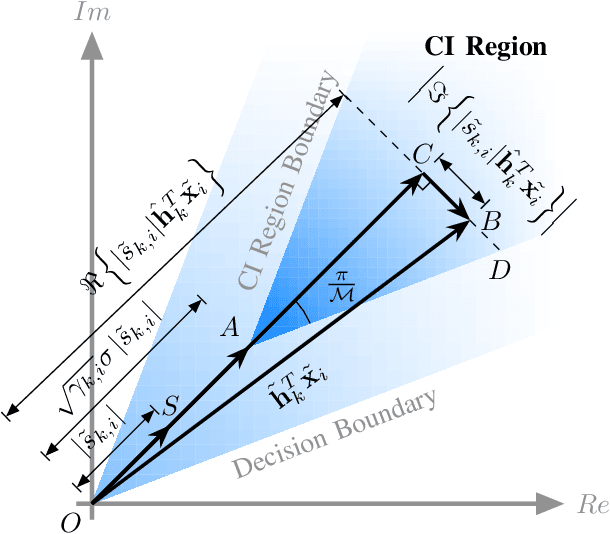
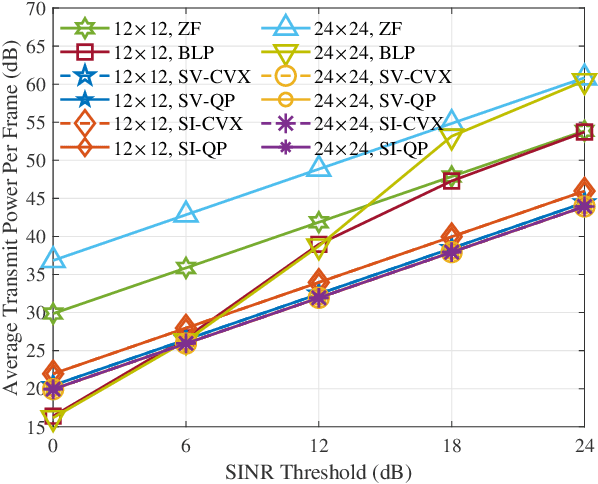
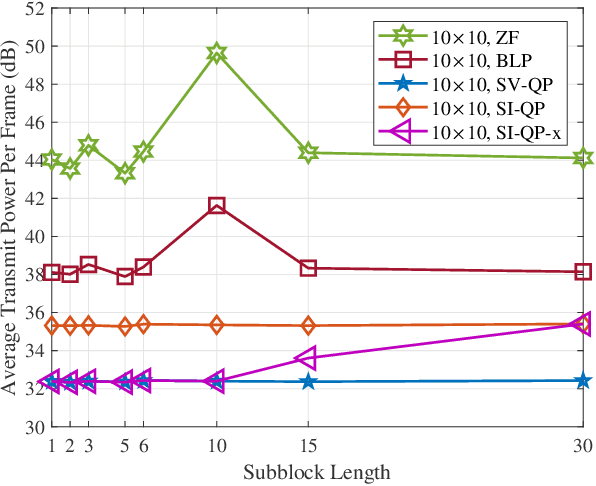
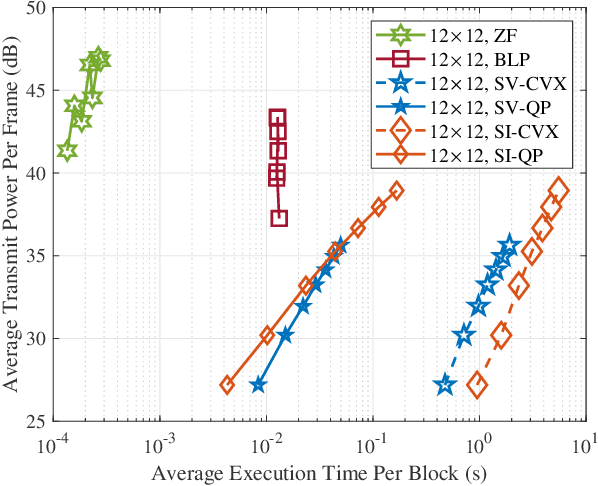
This paper investigates block-level interference exploitation (IE) precoding for multi-user multiple-input single-output (MU-MISO) downlink systems. To overcome the need for symbol-level IE precoding to frequently update the precoding matrix, we propose to jointly optimize all the precoders or transmit signals within a transmission block. The resultant precoders only need to be updated once per block, and while not necessarily constant over all the symbol slots, we refer to the technique as block-level slot-variant IE precoding. Through a careful examination of the optimal structure and the explicit duality inherent in block-level power minimization (PM) and signal-to-interference-plus-noise ratio (SINR) balancing (SB) problems, we discover that the joint optimization can be decomposed into subproblems with smaller variable sizes. As a step further, we propose block-level slot-invariant IE precoding by adding a structural constraint on the slot-variant IE precoding to maintain a constant precoder throughout the block. A novel linear precoder for IE is further presented, and we prove that the proposed slot-variant and slot-invariant IE precoding share an identical solution when the number of symbol slots does not exceed the number of users. Numerical simulations demonstrate that the proposed precoders achieve a significant complexity reduction compared against benchmark schemes, without sacrificing performance.

Nested Elimination: A Simple Algorithm for Best-Item Identification from Choice-Based Feedback

We study the problem of best-item identification from choice-based feedback. In this problem, a company sequentially and adaptively shows display sets to a population of customers and collects their choices. The objective is to identify the most preferred item with the least number of samples and at a high confidence level. We propose an elimination-based algorithm, namely Nested Elimination (NE), which is inspired by the nested structure implied by the information-theoretic lower bound. NE is simple in structure, easy to implement, and has a strong theoretical guarantee for sample complexity. Specifically, NE utilizes an innovative elimination criterion and circumvents the need to solve any complex combinatorial optimization problem. We provide an instance-specific and non-asymptotic bound on the expected sample complexity of NE. We also show NE achieves high-order worst-case asymptotic optimality. Finally, numerical experiments from both synthetic and real data corroborate our theoretical findings.

Speeding-up Symbol-Level Precoding Using Separable and Dual Optimizations

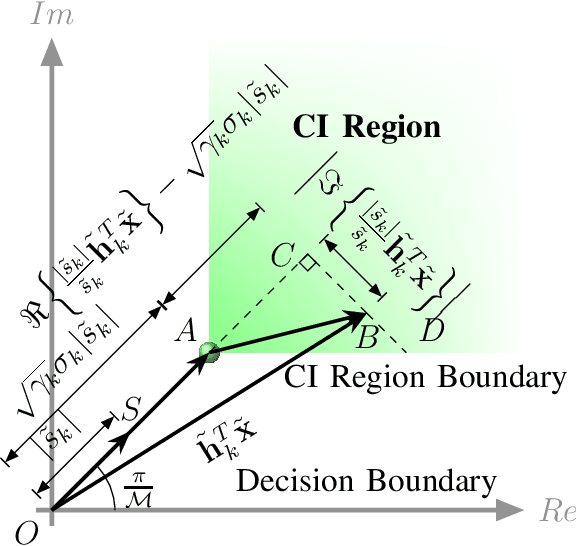
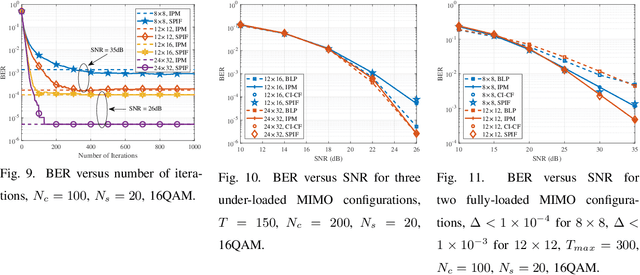
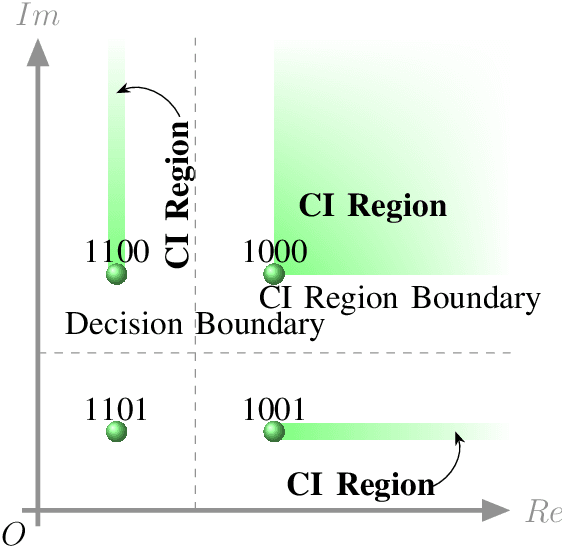
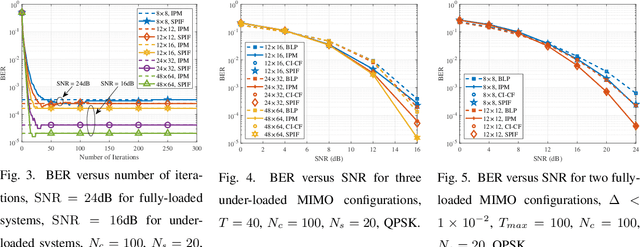
Symbol-level precoding (SLP) manipulates the transmitted signals to accurately exploit the multi-user interference (MUI) in the multi-user downlink. This enables that all the resultant interference contributes to correct detection, which is the so-called constructive interference (CI). Its performance superiority comes at the cost of solving a nonlinear optimization problem on a symbol-by-symbol basis, for which the resulting complexity becomes prohibitive in realistic wireless communication systems. In this paper, we investigate low-complexity SLP algorithms for both phase-shift keying (PSK) and quadrature amplitude modulation (QAM). Specifically, we first prove that the max-min SINR balancing (SB) SLP problem for PSK signaling is not separable, which is contrary to the power minimization (PM) SLP problem, and accordingly, existing decomposition methods are not applicable. Next, we establish an explicit duality between the PM-SLP and SB-SLP problems for PSK modulation. The proposed duality facilitates obtaining the solution to the SB-SLP given the solution to the PM-SLP without the need for one-dimension search, and vice versa. We then propose a closed-form power scaling algorithm to solve the SB-SLP via PM-SLP to take advantage of the separability of the PM-SLP. As for QAM modulation, we convert the PM-SLP problem into a separable equivalent optimization problem, and decompose the new problem into several simple parallel subproblems with closed-form solutions, leveraging the proximal Jacobian alternating direction method of multipliers (PJ-ADMM). We further prove that the proposed duality can be generalized to the multi-level modulation case, based on which a power scaling parallel inverse-free algorithm is also proposed to solve the SB-SLP for QAM signaling. Numerical results show that the proposed algorithms offer optimal performance with lower complexity than the state-of-the-art.

Optimal Clustering with Bandit Feedback

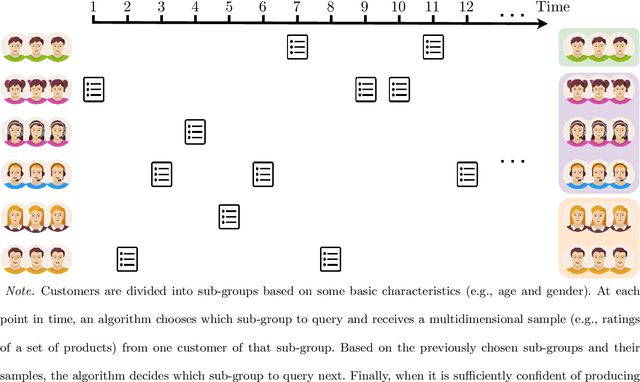
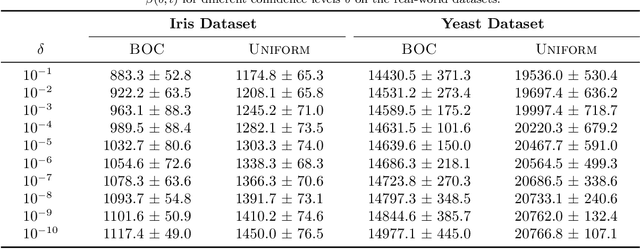
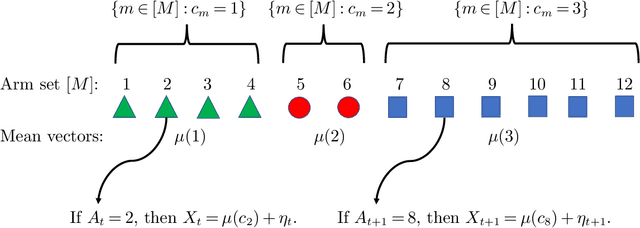
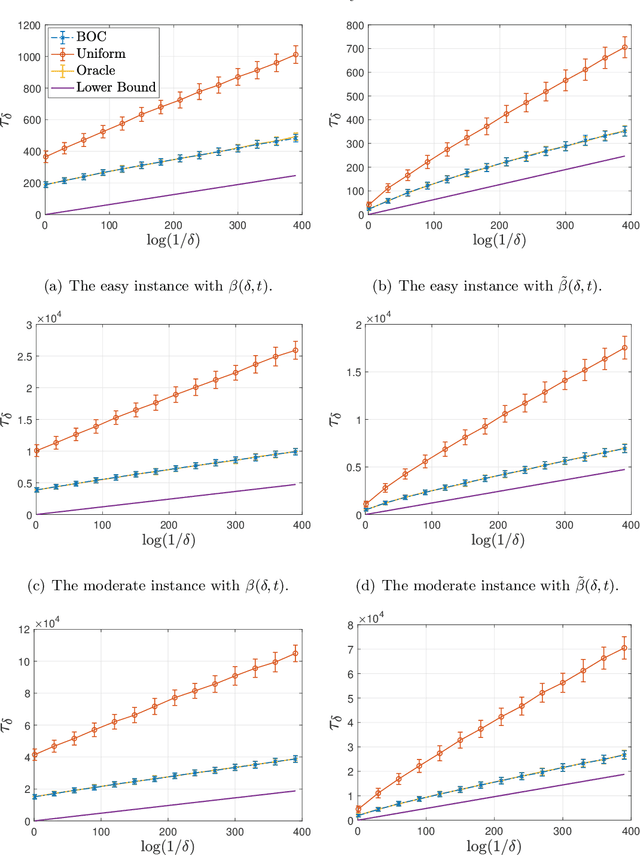
This paper considers the problem of online clustering with bandit feedback. A set of arms (or items) can be partitioned into various groups that are unknown. Within each group, the observations associated to each of the arms follow the same distribution with the same mean vector. At each time step, the agent queries or pulls an arm and obtains an independent observation from the distribution it is associated to. Subsequent pulls depend on previous ones as well as the previously obtained samples. The agent's task is to uncover the underlying partition of the arms with the least number of arm pulls and with a probability of error not exceeding a prescribed constant $\delta$. The problem proposed finds numerous applications from clustering of variants of viruses to online market segmentation. We present an instance-dependent information-theoretic lower bound on the expected sample complexity for this task, and design a computationally efficient and asymptotically optimal algorithm, namely Bandit Online Clustering (BOC). The algorithm includes a novel stopping rule for adaptive sequential testing that circumvents the need to exactly solve any NP-hard weighted clustering problem as its subroutines. We show through extensive simulations on synthetic and real-world datasets that BOC's performance matches the lower bound asymptotically, and significantly outperforms a non-adaptive baseline algorithm.

AutoPipeline: Synthesize Data Pipelines By-Target Using Reinforcement Learning and Search

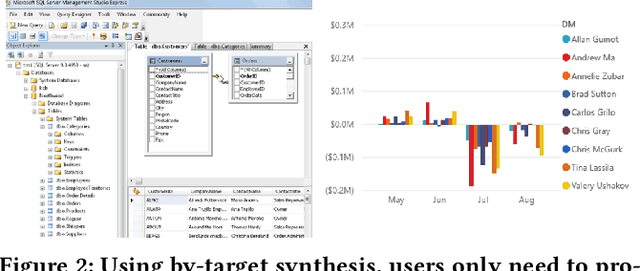
Recent work has made significant progress in helping users to automate single data preparation steps, such as string-transformations and table-manipulation operators (e.g., Join, GroupBy, Pivot, etc.). We in this work propose to automate multiple such steps end-to-end, by synthesizing complex data pipelines with both string transformations and table-manipulation operators. We propose a novel "by-target" paradigm that allows users to easily specify the desired pipeline, which is a significant departure from the traditional by-example paradigm. Using by-target, users would provide input tables (e.g., csv or json files), and point us to a "target table" (e.g., an existing database table or BI dashboard) to demonstrate how the output from the desired pipeline would schematically "look like". While the problem is seemingly underspecified, our unique insight is that implicit table constraints such as FDs and keys can be exploited to significantly constrain the space to make the problem tractable. We develop an Auto-Pipeline system that learns to synthesize pipelines using reinforcement learning and search. Experiments on large numbers of real pipelines crawled from GitHub suggest that Auto-Pipeline can successfully synthesize 60-70% of these complex pipelines (up to 10 steps) in 10-20 seconds on average.

Towards Minimax Optimal Best Arm Identification in Linear Bandits

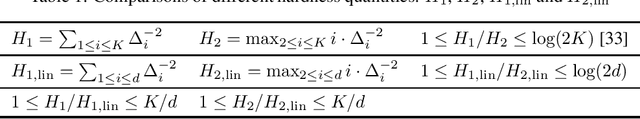
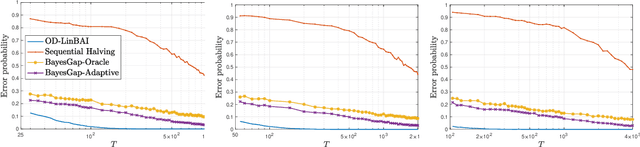
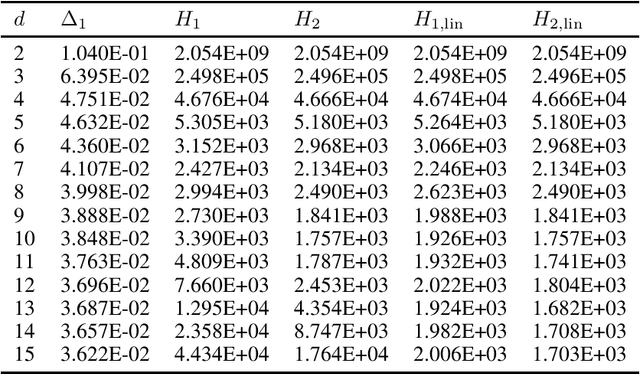
We study the problem of best arm identification in linear bandits in the fixed-budget setting. By leveraging properties of the G-optimal design and incorporating it into the arm allocation rule, we design a parameter-free algorithm, Optimal Design-based Linear Best Arm Identification (OD-LinBAI). We provide a theoretical analysis of the failure probability of OD-LinBAI. While the performances of existing methods (e.g., BayesGap) depend on all the optimality gaps, OD-LinBAI depends on the gaps of the top $d$ arms, where $d$ is the effective dimension of the linear bandit instance. Furthermore, we present a minimax lower bound for this problem. The upper and lower bounds show that OD-LinBAI is minimax optimal up to multiplicative factors in the exponent. Finally, numerical experiments corroborate our theoretical findings.