Almost Minimax Optimal Best Arm Identification in Piecewise Stationary Linear Bandits

We propose a {\em novel} piecewise stationary linear bandit (PSLB) model, where the environment randomly samples a context from an unknown probability distribution at each changepoint, and the quality of an arm is measured by its return averaged over all contexts. The contexts and their distribution, as well as the changepoints are unknown to the agent. We design {\em Piecewise-Stationary $\varepsilon$-Best Arm Identification$^+$} (PS$\varepsilon$BAI$^+$), an algorithm that is guaranteed to identify an $\varepsilon$-optimal arm with probability $\ge 1-\delta$ and with a minimal number of samples. PS$\varepsilon$BAI$^+$ consists of two subroutines, PS$\varepsilon$BAI and {\sc Na\"ive $\varepsilon$-BAI} (N$\varepsilon$BAI), which are executed in parallel. PS$\varepsilon$BAI actively detects changepoints and aligns contexts to facilitate the arm identification process. When PS$\varepsilon$BAI and N$\varepsilon$BAI are utilized judiciously in parallel, PS$\varepsilon$BAI$^+$ is shown to have a finite expected sample complexity. By proving a lower bound, we show the expected sample complexity of PS$\varepsilon$BAI$^+$ is optimal up to a logarithmic factor. We compare PS$\varepsilon$BAI$^+$ to baseline algorithms using numerical experiments which demonstrate its efficiency. Both our analytical and numerical results corroborate that the efficacy of PS$\varepsilon$BAI$^+$ is due to the delicate change detection and context alignment procedures embedded in PS$\varepsilon$BAI.

Stochastic Gradient Succeeds for Bandits

We show that the \emph{stochastic gradient} bandit algorithm converges to a \emph{globally optimal} policy at an $O(1/t)$ rate, even with a \emph{constant} step size. Remarkably, global convergence of the stochastic gradient bandit algorithm has not been previously established, even though it is an old algorithm known to be applicable to bandits. The new result is achieved by establishing two novel technical findings: first, the noise of the stochastic updates in the gradient bandit algorithm satisfies a strong ``growth condition'' property, where the variance diminishes whenever progress becomes small, implying that additional noise control via diminishing step sizes is unnecessary; second, a form of ``weak exploration'' is automatically achieved through the stochastic gradient updates, since they prevent the action probabilities from decaying faster than $O(1/t)$, thus ensuring that every action is sampled infinitely often with probability $1$. These two findings can be used to show that the stochastic gradient update is already ``sufficient'' for bandits in the sense that exploration versus exploitation is automatically balanced in a manner that ensures almost sure convergence to a global optimum. These novel theoretical findings are further verified by experimental results.

Probably Anytime-Safe Stochastic Combinatorial Semi-Bandits

Motivated by concerns about making online decisions that incur undue amount of risk at each time step, in this paper, we formulate the probably anytime-safe stochastic combinatorial semi-bandits problem. In this problem, the agent is given the option to select a subset of size at most $K$ from a set of $L$ ground items. Each item is associated to a certain mean reward as well as a variance that represents its risk. To mitigate the risk that the agent incurs, we require that with probability at least $1-\delta$, over the entire horizon of time $T$, each of the choices that the agent makes should contain items whose sum of variances does not exceed a certain variance budget. We call this probably anytime-safe constraint. Under this constraint, we design and analyze an algorithm {\sc PASCombUCB} that minimizes the regret over the horizon of time $T$. By developing accompanying information-theoretic lower bounds, we show under both the problem-dependent and problem-independent paradigms, {\sc PASCombUCB} is almost asymptotically optimal. Our problem setup, the proposed {\sc PASCombUCB} algorithm, and novel analyses are applicable to domains such as recommendation systems and transportation in which an agent is allowed to choose multiple items at a single time step and wishes to control the risk over the whole time horizon.

Fast Beam Alignment via Pure Exploration in Multi-armed Bandits

The beam alignment (BA) problem consists in accurately aligning the transmitter and receiver beams to establish a reliable communication link in wireless communication systems. Existing BA methods search the entire beam space to identify the optimal transmit-receive beam pair. This incurs a significant latency when the number of antennas is large. In this work, we develop a bandit-based fast BA algorithm to reduce BA latency for millimeter-wave (mmWave) communications. Our algorithm is named Two-Phase Heteroscedastic Track-and-Stop (2PHT\&S). We first formulate the BA problem as a pure exploration problem in multi-armed bandits in which the objective is to minimize the required number of time steps given a certain fixed confidence level. By taking advantage of the correlation structure among beams that the information from nearby beams is similar and the heteroscedastic property that the variance of the reward of an arm (beam) is related to its mean, the proposed algorithm groups all beams into several beam sets such that the optimal beam set is first selected and the optimal beam is identified in this set after that. Theoretical analysis and simulation results on synthetic and semi-practical channel data demonstrate the clear superiority of the proposed algorithm vis-\`a-vis other baseline competitors.

Optimal Clustering with Bandit Feedback

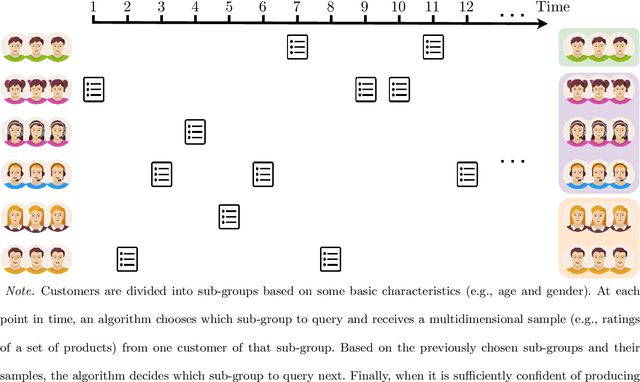
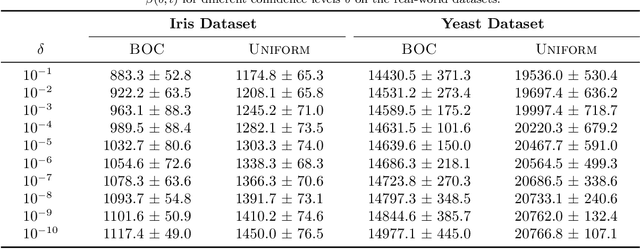
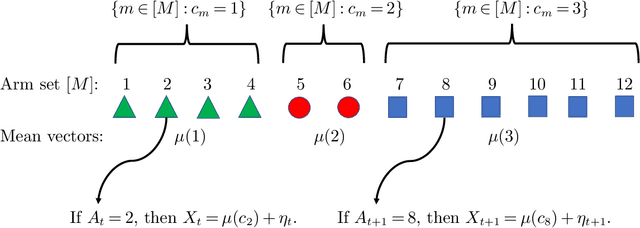
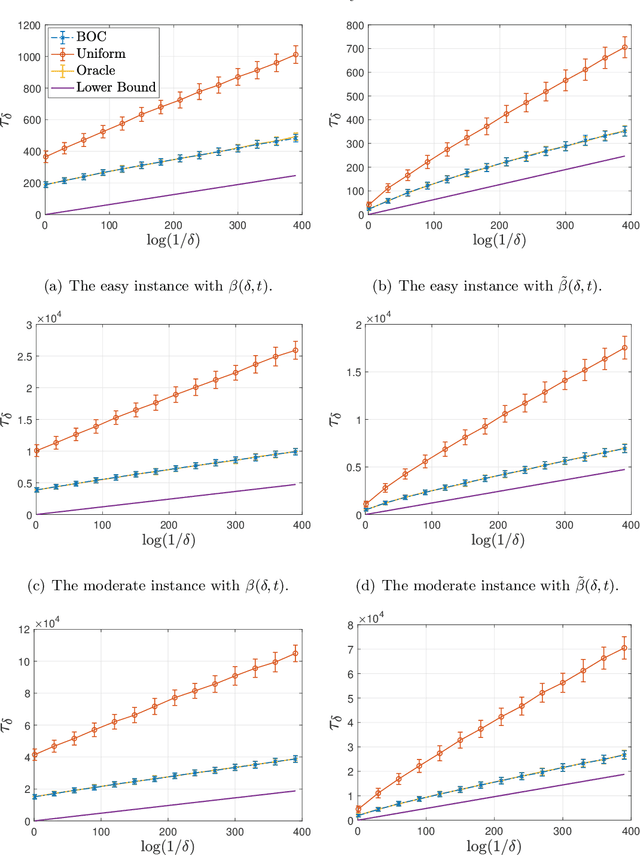
This paper considers the problem of online clustering with bandit feedback. A set of arms (or items) can be partitioned into various groups that are unknown. Within each group, the observations associated to each of the arms follow the same distribution with the same mean vector. At each time step, the agent queries or pulls an arm and obtains an independent observation from the distribution it is associated to. Subsequent pulls depend on previous ones as well as the previously obtained samples. The agent's task is to uncover the underlying partition of the arms with the least number of arm pulls and with a probability of error not exceeding a prescribed constant $\delta$. The problem proposed finds numerous applications from clustering of variants of viruses to online market segmentation. We present an instance-dependent information-theoretic lower bound on the expected sample complexity for this task, and design a computationally efficient and asymptotically optimal algorithm, namely Bandit Online Clustering (BOC). The algorithm includes a novel stopping rule for adaptive sequential testing that circumvents the need to exactly solve any NP-hard weighted clustering problem as its subroutines. We show through extensive simulations on synthetic and real-world datasets that BOC's performance matches the lower bound asymptotically, and significantly outperforms a non-adaptive baseline algorithm.

Almost Optimal Variance-Constrained Best Arm Identification

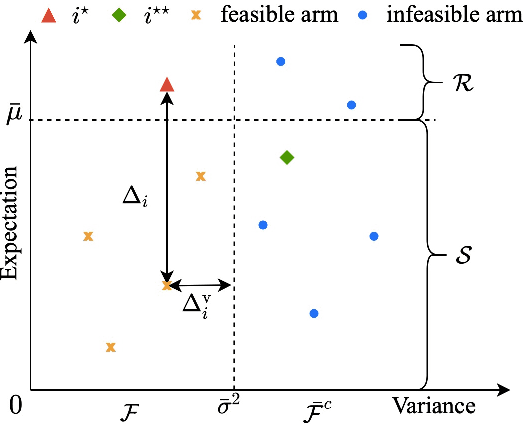
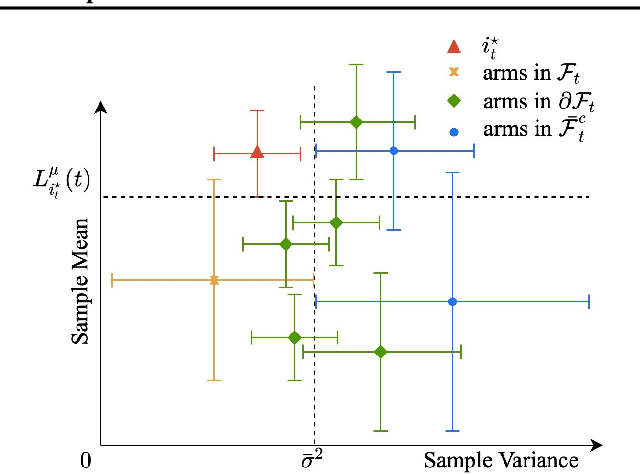
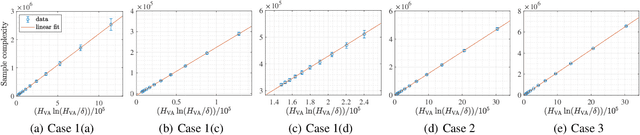
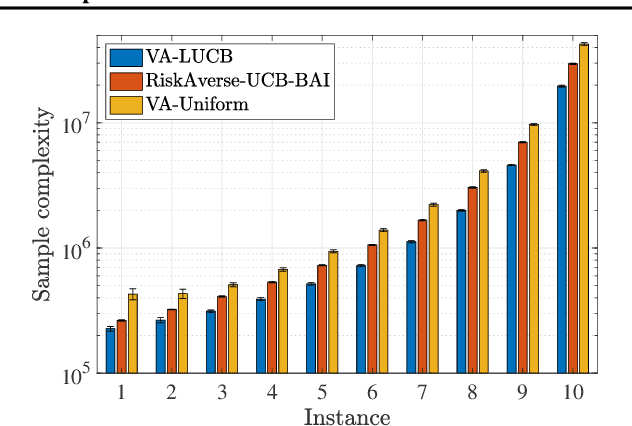
We design and analyze VA-LUCB, a parameter-free algorithm, for identifying the best arm under the fixed-confidence setup and under a stringent constraint that the variance of the chosen arm is strictly smaller than a given threshold. An upper bound on VA-LUCB's sample complexity is shown to be characterized by a fundamental variance-aware hardness quantity $H_{VA}$. By proving a lower bound, we show that sample complexity of VA-LUCB is optimal up to a factor logarithmic in $H_{VA}$. Extensive experiments corroborate the dependence of the sample complexity on the various terms in $H_{VA}$. By comparing VA-LUCB's empirical performance to a close competitor RiskAverse-UCB-BAI by David et al. (2018), our experiments suggest that VA-LUCB has the lowest sample complexity for this class of risk-constrained best arm identification problems, especially for the riskiest instances.

On the Pareto Frontier of Regret Minimization and Best Arm Identification in Stochastic Bandits

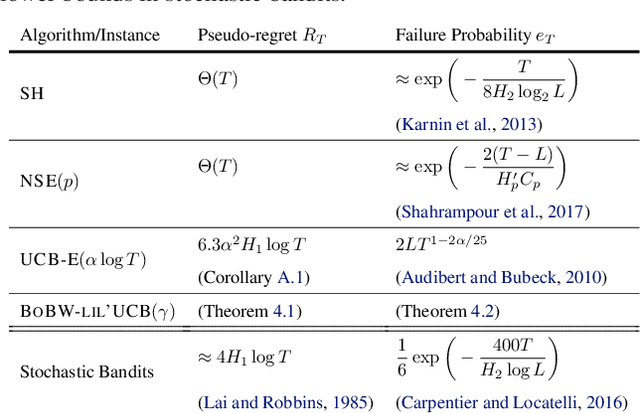
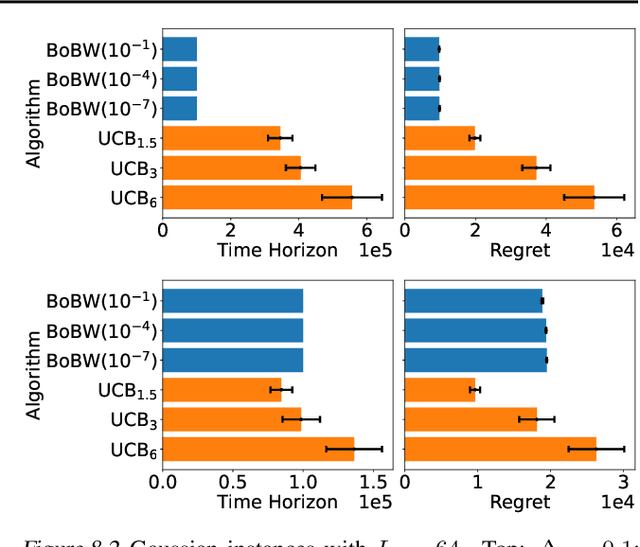
We study the Pareto frontier of two archetypal objectives in stochastic bandits, namely, regret minimization (RM) and best arm identification (BAI) with a fixed horizon. It is folklore that the balance between exploitation and exploration is crucial for both RM and BAI, but exploration is more critical in achieving the optimal performance for the latter objective. To make this precise, we first design and analyze the BoBW-lil'UCB$({\gamma})$ algorithm, which achieves order-wise optimal performance for RM or BAI under different values of ${\gamma}$. Complementarily, we show that no algorithm can simultaneously perform optimally for both the RM and BAI objectives. More precisely, we establish non-trivial lower bounds on the regret achievable by any algorithm with a given BAI failure probability. This analysis shows that in some regimes BoBW-lil'UCB$({\gamma})$ achieves Pareto-optimality up to constant or small terms. Numerical experiments further demonstrate that when applied to difficult instances, BoBW-lil'UCB outperforms a close competitor UCB$_{\alpha}$ (Degenne et al., 2019), which is designed for RM and BAI with a fixed confidence.

Probabilistic Sequential Shrinking: A Best Arm Identification Algorithm for Stochastic Bandits with Corruptions

We consider a best arm identification (BAI) problem for stochastic bandits with adversarial corruptions in the fixed-budget setting of $T$ steps. We design a novel randomized algorithm, Probabilistic Sequential Shrinking$(u)$ (PSS$(u)$), which is agnostic to the amount of corruptions. When the amount of corruptions per step (CPS) is below a threshold, PSS$(u)$ identifies the best arm or item with probability tending to $1$ as $T\rightarrow\infty$. Otherwise, the optimality gap of the identified item degrades gracefully with the CPS. We argue that such a bifurcation is necessary. In addition, we show that when the CPS is sufficiently large, no algorithm can achieve a BAI probability tending to $1$ as $T\rightarrow \infty$. In PSS$(u)$, the parameter $u$ serves to balance between the optimality gap and success probability. En route, the injection of randomization is shown to be essential to mitigate the impact of corruptions. Indeed, we show that PSS$(u)$ has a better performance than its deterministic analogue, the Successive Halving (SH) algorithm by Karnin et al. (2013). PSS$(2)$'s performance guarantee matches SH's when there is no corruption. Finally, we identify a term in the exponent of the failure probability of PSS$(u)$ that generalizes the common $H_2$ term for BAI under the fixed-budget setting.

Best Arm Identification for Cascading Bandits in the Fixed Confidence Setting

We design and analyze CascadeBAI, an algorithm for finding the best set of $K$ items, also called an arm, within the framework of cascading bandits. An upper bound on the time complexity of CascadeBAI is derived by overcoming a crucial analytical challenge, namely, that of probabilistically estimating the amount of available feedback at each step. To do so, we define a new class of random variables (r.v.'s) which we term as left-sided sub-Gaussian r.v.'s; these are r.v.'s whose cumulant generating functions (CGFs) can be bounded by a quadratic only for non-positive arguments of the CGFs. This enables the application of a sufficiently tight Bernstein-type concentration inequality. We show, through the derivation of a lower bound on the time complexity, that the performance of CascadeBAI is optimal in some practical regimes. Finally, extensive numerical simulations corroborate the efficacy of CascadeBAI as well as the tightness of our upper bound on its time complexity.

Thompson Sampling for Cascading Bandits

We design and analyze TS-Cascade, a Thompson sampling algorithm for the cascading bandit problem. In TS-Cascade, Bayesian estimates of the click probability are constructed using a univariate Gaussian; this leads to a more efficient exploration procedure vis-\`a-vis existing UCB-based approaches. We also incorporate the empirical variance of each item's click probability into the Bayesian updates. These two novel features allow us to prove an expected regret bound of the form $\tilde{O}(\sqrt{KLT})$ where $L$ and $K$ are the number of ground items and the number of items in the chosen list respectively and $T\ge L$ is the number of Thompson sampling update steps. This matches the state-of-the-art regret bounds for UCB-based algorithms. More importantly, it is the first theoretical guarantee on a Thompson sampling algorithm for any stochastic combinatorial bandit problem model with partial feedback. Empirical experiments demonstrate superiority of TS-Cascade compared to existing UCB-based procedures in terms of the expected cumulative regret and the time complexity.