On the Pareto Frontier of Regret Minimization and Best Arm Identification in Stochastic Bandits

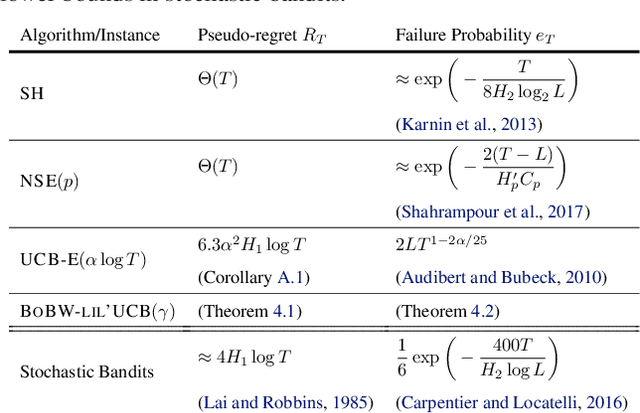
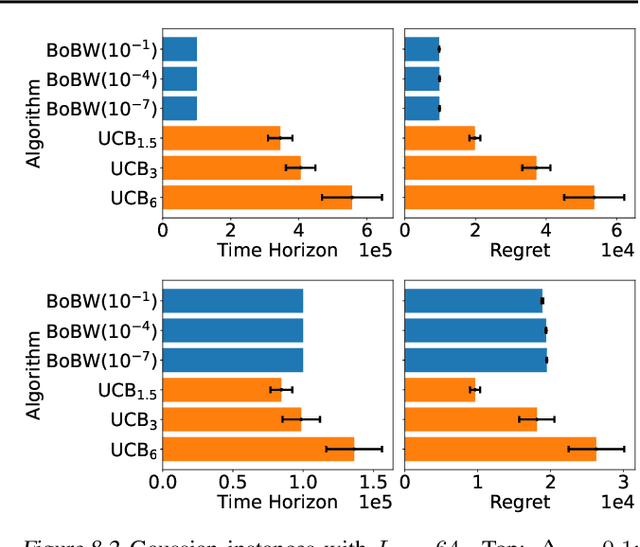
We study the Pareto frontier of two archetypal objectives in stochastic bandits, namely, regret minimization (RM) and best arm identification (BAI) with a fixed horizon. It is folklore that the balance between exploitation and exploration is crucial for both RM and BAI, but exploration is more critical in achieving the optimal performance for the latter objective. To make this precise, we first design and analyze the BoBW-lil'UCB$({\gamma})$ algorithm, which achieves order-wise optimal performance for RM or BAI under different values of ${\gamma}$. Complementarily, we show that no algorithm can simultaneously perform optimally for both the RM and BAI objectives. More precisely, we establish non-trivial lower bounds on the regret achievable by any algorithm with a given BAI failure probability. This analysis shows that in some regimes BoBW-lil'UCB$({\gamma})$ achieves Pareto-optimality up to constant or small terms. Numerical experiments further demonstrate that when applied to difficult instances, BoBW-lil'UCB outperforms a close competitor UCB$_{\alpha}$ (Degenne et al., 2019), which is designed for RM and BAI with a fixed confidence.