Near Optimal Non-asymptotic Sample Complexity of 1-Identification

Motivated by an open direction in existing literature, we study the 1-identification problem, a fundamental multi-armed bandit formulation on pure exploration. The goal is to determine whether there exists an arm whose mean reward is at least a known threshold $\mu_0$, or to output None if it believes such an arm does not exist. The agent needs to guarantee its output is correct with probability at least $1-\delta$. Degenne & Koolen 2019 has established the asymptotically tight sample complexity for the 1-identification problem, but they commented that the non-asymptotic analysis remains unclear. We design a new algorithm Sequential-Exploration-Exploitation (SEE), and conduct theoretical analysis from the non-asymptotic perspective. Novel to the literature, we achieve near optimality, in the sense of matching upper and lower bounds on the pulling complexity. The gap between the upper and lower bounds is up to a polynomial logarithmic factor. The numerical result also indicates the effectiveness of our algorithm, compared to existing benchmarks.

Best Arm Identification with Possibly Biased Offline Data

We study the best arm identification (BAI) problem with potentially biased offline data in the fixed confidence setting, which commonly arises in real-world scenarios such as clinical trials. We prove an impossibility result for adaptive algorithms without prior knowledge of the bias bound between online and offline distributions. To address this, we propose the LUCB-H algorithm, which introduces adaptive confidence bounds by incorporating an auxiliary bias correction to balance offline and online data within the LUCB framework. Theoretical analysis shows that LUCB-H matches the sample complexity of standard LUCB when offline data is misleading and significantly outperforms it when offline data is helpful. We also derive an instance-dependent lower bound that matches the upper bound of LUCB-H in certain scenarios. Numerical experiments further demonstrate the robustness and adaptability of LUCB-H in effectively incorporating offline data.

Efficiently Solving Discounted MDPs with Predictions on Transition Matrices

We study infinite-horizon Discounted Markov Decision Processes (DMDPs) under a generative model. Motivated by the Algorithm with Advice framework Mitzenmacher and Vassilvitskii 2022, we propose a novel framework to investigate how a prediction on the transition matrix can enhance the sample efficiency in solving DMDPs and improve sample complexity bounds. We focus on the DMDPs with $N$ state-action pairs and discounted factor $\gamma$. Firstly, we provide an impossibility result that, without prior knowledge of the prediction accuracy, no sampling policy can compute an $\epsilon$-optimal policy with a sample complexity bound better than $\tilde{O}((1-\gamma)^{-3} N\epsilon^{-2})$, which matches the state-of-the-art minimax sample complexity bound with no prediction. In complement, we propose an algorithm based on minimax optimization techniques that leverages the prediction on the transition matrix. Our algorithm achieves a sample complexity bound depending on the prediction error, and the bound is uniformly better than $\tilde{O}((1-\gamma)^{-4} N \epsilon^{-2})$, the previous best result derived from convex optimization methods. These theoretical findings are further supported by our numerical experiments.

Leveraging (Biased) Information: Multi-armed Bandits with Offline Data

We leverage offline data to facilitate online learning in stochastic multi-armed bandits. The probability distributions that govern the offline data and the online rewards can be different. Without any non-trivial upper bound on their difference, we show that no non-anticipatory policy can outperform the UCB policy by (Auer et al. 2002), even in the presence of offline data. In complement, we propose an online policy MIN-UCB, which outperforms UCB when a non-trivial upper bound is given. MIN-UCB adaptively chooses to utilize the offline data when they are deemed informative, and to ignore them otherwise. MIN-UCB is shown to be tight in terms of both instance independent and dependent regret bounds. Finally, we corroborate the theoretical results with numerical experiments.

Best Arm Identification with Resource Constraints

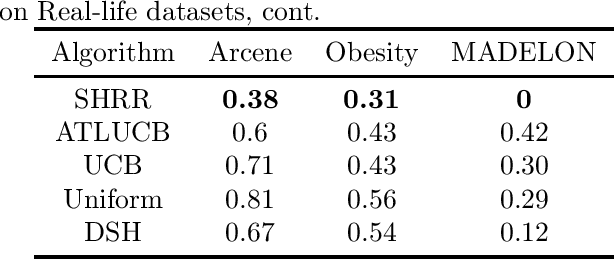
Motivated by the cost heterogeneity in experimentation across different alternatives, we study the Best Arm Identification with Resource Constraints (BAIwRC) problem. The agent aims to identify the best arm under resource constraints, where resources are consumed for each arm pull. We make two novel contributions. We design and analyze the Successive Halving with Resource Rationing algorithm (SH-RR). The SH-RR achieves a near-optimal non-asymptotic rate of convergence in terms of the probability of successively identifying an optimal arm. Interestingly, we identify a difference in convergence rates between the cases of deterministic and stochastic resource consumption.

Non-Stationary Bandits with Knapsack Problems with Advice

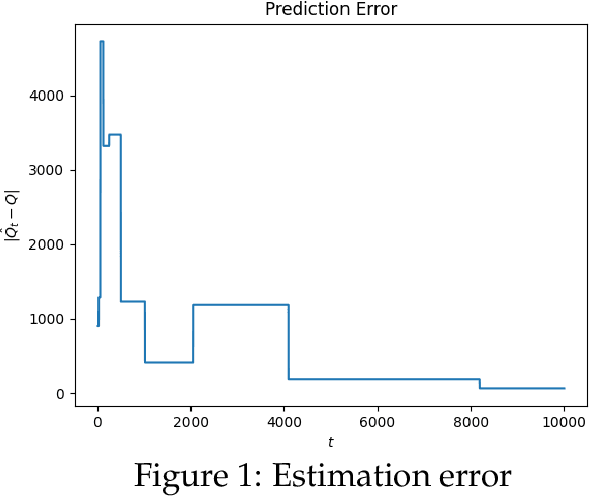
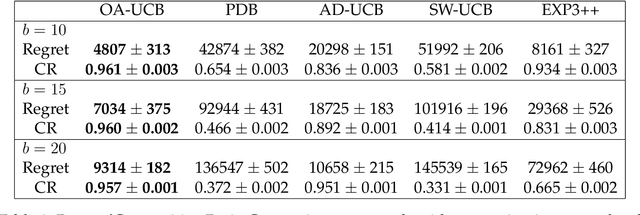
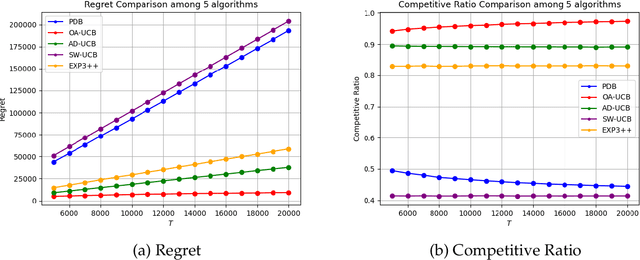
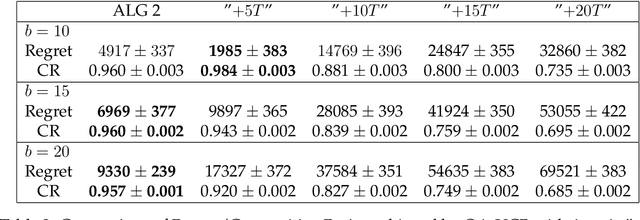
We consider a non-stationary Bandits with Knapsack problem. The outcome distribution at each time is scaled by a non-stationary quantity that signifies changing demand volumes. Instead of studying settings with limited non-stationarity, we investigate how online predictions on the total demand volume $Q$ allows us to improve our performance guarantees. We show that, without any prediction, any online algorithm incurs a linear-in-$T$ regret. In contrast, with online predictions on $Q$, we propose an online algorithm that judiciously incorporates the predictions, and achieve regret bounds that depends on the accuracy of the predictions. These bounds are shown to be tight in settings when prediction accuracy improves across time. Our theoretical results are corroborated by our numerical findings.

On the Pareto Frontier of Regret Minimization and Best Arm Identification in Stochastic Bandits

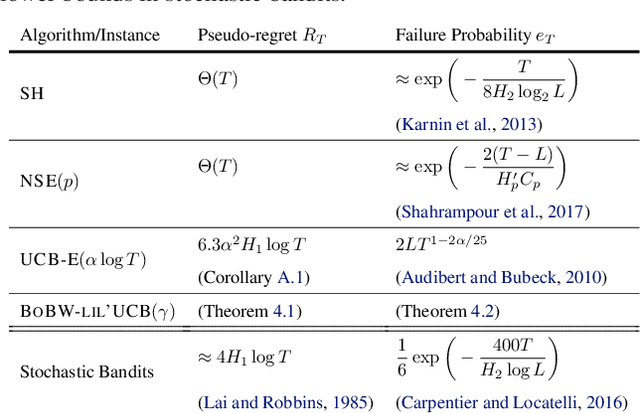
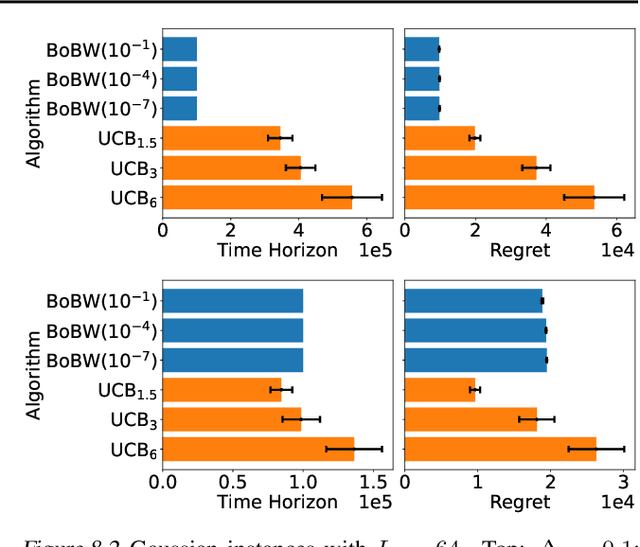
We study the Pareto frontier of two archetypal objectives in stochastic bandits, namely, regret minimization (RM) and best arm identification (BAI) with a fixed horizon. It is folklore that the balance between exploitation and exploration is crucial for both RM and BAI, but exploration is more critical in achieving the optimal performance for the latter objective. To make this precise, we first design and analyze the BoBW-lil'UCB$({\gamma})$ algorithm, which achieves order-wise optimal performance for RM or BAI under different values of ${\gamma}$. Complementarily, we show that no algorithm can simultaneously perform optimally for both the RM and BAI objectives. More precisely, we establish non-trivial lower bounds on the regret achievable by any algorithm with a given BAI failure probability. This analysis shows that in some regimes BoBW-lil'UCB$({\gamma})$ achieves Pareto-optimality up to constant or small terms. Numerical experiments further demonstrate that when applied to difficult instances, BoBW-lil'UCB outperforms a close competitor UCB$_{\alpha}$ (Degenne et al., 2019), which is designed for RM and BAI with a fixed confidence.

Probabilistic Sequential Shrinking: A Best Arm Identification Algorithm for Stochastic Bandits with Corruptions

We consider a best arm identification (BAI) problem for stochastic bandits with adversarial corruptions in the fixed-budget setting of $T$ steps. We design a novel randomized algorithm, Probabilistic Sequential Shrinking$(u)$ (PSS$(u)$), which is agnostic to the amount of corruptions. When the amount of corruptions per step (CPS) is below a threshold, PSS$(u)$ identifies the best arm or item with probability tending to $1$ as $T\rightarrow\infty$. Otherwise, the optimality gap of the identified item degrades gracefully with the CPS. We argue that such a bifurcation is necessary. In addition, we show that when the CPS is sufficiently large, no algorithm can achieve a BAI probability tending to $1$ as $T\rightarrow \infty$. In PSS$(u)$, the parameter $u$ serves to balance between the optimality gap and success probability. En route, the injection of randomization is shown to be essential to mitigate the impact of corruptions. Indeed, we show that PSS$(u)$ has a better performance than its deterministic analogue, the Successive Halving (SH) algorithm by Karnin et al. (2013). PSS$(2)$'s performance guarantee matches SH's when there is no corruption. Finally, we identify a term in the exponent of the failure probability of PSS$(u)$ that generalizes the common $H_2$ term for BAI under the fixed-budget setting.

Reinforcement Learning for Non-Stationary Markov Decision Processes: The Blessing of (More) Optimism

We consider un-discounted reinforcement learning (RL) in Markov decision processes (MDPs) under drifting non-stationarity, i.e., both the reward and state transition distributions are allowed to evolve over time, as long as their respective total variations, quantified by suitable metrics, do not exceed certain variation budgets. We first develop the Sliding Window Upper-Confidence bound for Reinforcement Learning with Confidence Widening (SWUCRL2-CW) algorithm, and establish its dynamic regret bound when the variation budgets are known. In addition, we propose the Bandit-over-Reinforcement Learning (BORL) algorithm to adaptively tune the SWUCRL2-CW algorithm to achieve the same dynamic regret bound, but in a parameter-free manner, i.e., without knowing the variation budgets. Notably, learning non-stationary MDPs via the conventional optimistic exploration technique presents a unique challenge absent in existing (non-stationary) bandit learning settings. We overcome the challenge by a novel confidence widening technique that incorporates additional optimism.

Best Arm Identification for Cascading Bandits in the Fixed Confidence Setting

We design and analyze CascadeBAI, an algorithm for finding the best set of $K$ items, also called an arm, within the framework of cascading bandits. An upper bound on the time complexity of CascadeBAI is derived by overcoming a crucial analytical challenge, namely, that of probabilistically estimating the amount of available feedback at each step. To do so, we define a new class of random variables (r.v.'s) which we term as left-sided sub-Gaussian r.v.'s; these are r.v.'s whose cumulant generating functions (CGFs) can be bounded by a quadratic only for non-positive arguments of the CGFs. This enables the application of a sufficiently tight Bernstein-type concentration inequality. We show, through the derivation of a lower bound on the time complexity, that the performance of CascadeBAI is optimal in some practical regimes. Finally, extensive numerical simulations corroborate the efficacy of CascadeBAI as well as the tightness of our upper bound on its time complexity.