Efficiently Solving Discounted MDPs with Predictions on Transition Matrices

We study infinite-horizon Discounted Markov Decision Processes (DMDPs) under a generative model. Motivated by the Algorithm with Advice framework Mitzenmacher and Vassilvitskii 2022, we propose a novel framework to investigate how a prediction on the transition matrix can enhance the sample efficiency in solving DMDPs and improve sample complexity bounds. We focus on the DMDPs with $N$ state-action pairs and discounted factor $\gamma$. Firstly, we provide an impossibility result that, without prior knowledge of the prediction accuracy, no sampling policy can compute an $\epsilon$-optimal policy with a sample complexity bound better than $\tilde{O}((1-\gamma)^{-3} N\epsilon^{-2})$, which matches the state-of-the-art minimax sample complexity bound with no prediction. In complement, we propose an algorithm based on minimax optimization techniques that leverages the prediction on the transition matrix. Our algorithm achieves a sample complexity bound depending on the prediction error, and the bound is uniformly better than $\tilde{O}((1-\gamma)^{-4} N \epsilon^{-2})$, the previous best result derived from convex optimization methods. These theoretical findings are further supported by our numerical experiments.

Leveraging (Biased) Information: Multi-armed Bandits with Offline Data

We leverage offline data to facilitate online learning in stochastic multi-armed bandits. The probability distributions that govern the offline data and the online rewards can be different. Without any non-trivial upper bound on their difference, we show that no non-anticipatory policy can outperform the UCB policy by (Auer et al. 2002), even in the presence of offline data. In complement, we propose an online policy MIN-UCB, which outperforms UCB when a non-trivial upper bound is given. MIN-UCB adaptively chooses to utilize the offline data when they are deemed informative, and to ignore them otherwise. MIN-UCB is shown to be tight in terms of both instance independent and dependent regret bounds. Finally, we corroborate the theoretical results with numerical experiments.

Non-Stationary Bandits with Knapsack Problems with Advice

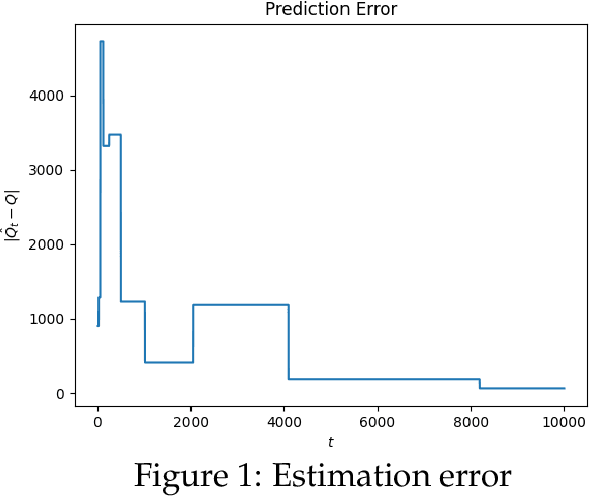
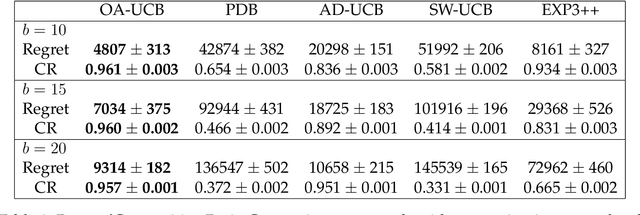
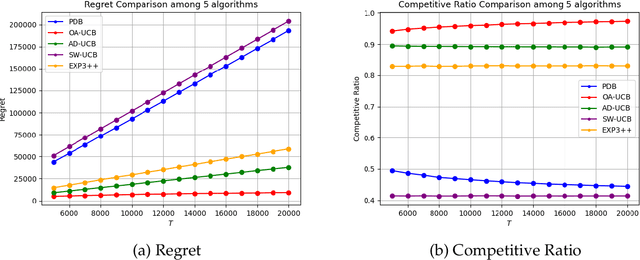
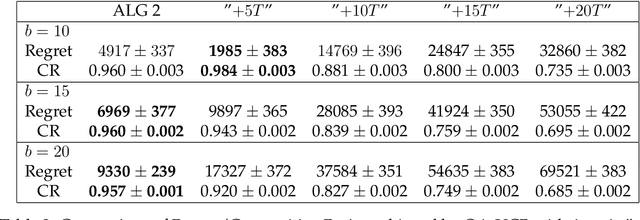
We consider a non-stationary Bandits with Knapsack problem. The outcome distribution at each time is scaled by a non-stationary quantity that signifies changing demand volumes. Instead of studying settings with limited non-stationarity, we investigate how online predictions on the total demand volume $Q$ allows us to improve our performance guarantees. We show that, without any prediction, any online algorithm incurs a linear-in-$T$ regret. In contrast, with online predictions on $Q$, we propose an online algorithm that judiciously incorporates the predictions, and achieve regret bounds that depends on the accuracy of the predictions. These bounds are shown to be tight in settings when prediction accuracy improves across time. Our theoretical results are corroborated by our numerical findings.