BanditSpec: Adaptive Speculative Decoding via Bandit Algorithms

Speculative decoding has emerged as a popular method to accelerate the inference of Large Language Models (LLMs) while retaining their superior text generation performance. Previous methods either adopt a fixed speculative decoding configuration regardless of the prefix tokens, or train draft models in an offline or online manner to align them with the context. This paper proposes a training-free online learning framework to adaptively choose the configuration of the hyperparameters for speculative decoding as text is being generated. We first formulate this hyperparameter selection problem as a Multi-Armed Bandit problem and provide a general speculative decoding framework BanditSpec. Furthermore, two bandit-based hyperparameter selection algorithms, UCBSpec and EXP3Spec, are designed and analyzed in terms of a novel quantity, the stopping time regret. We upper bound this regret under both stochastic and adversarial reward settings. By deriving an information-theoretic impossibility result, it is shown that the regret performance of UCBSpec is optimal up to universal constants. Finally, extensive empirical experiments with LLaMA3 and Qwen2 demonstrate that our algorithms are effective compared to existing methods, and the throughput is close to the oracle best hyperparameter in simulated real-life LLM serving scenarios with diverse input prompts.

Enhancing Multi-Text Long Video Generation Consistency without Tuning: Time-Frequency Analysis, Prompt Alignment, and Theory

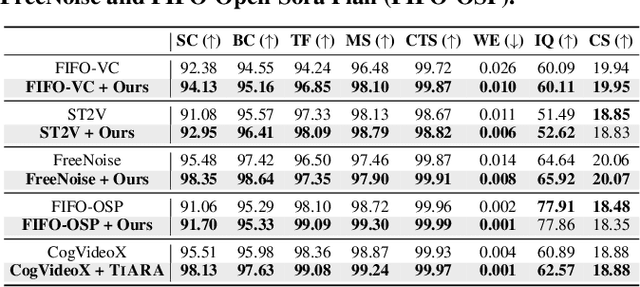
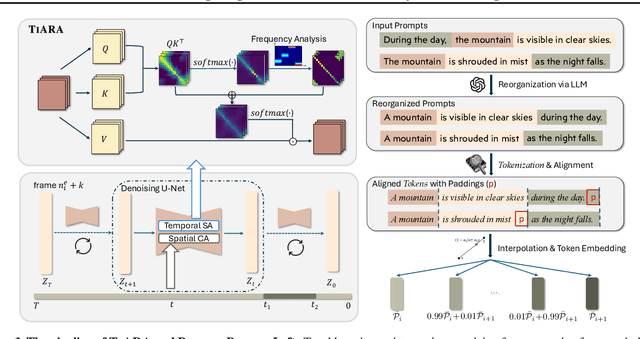
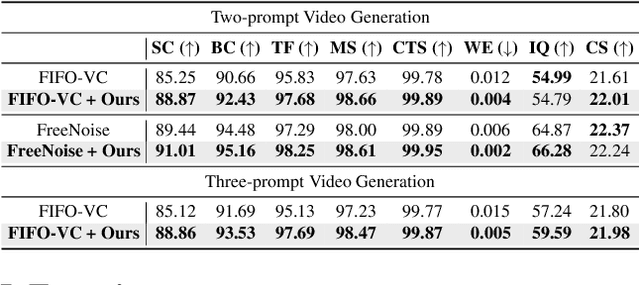
Despite the considerable progress achieved in the long video generation problem, there is still significant room to improve the consistency of the videos, particularly in terms of smoothness and transitions between scenes. We address these issues to enhance the consistency and coherence of videos generated with either single or multiple prompts. We propose the Time-frequency based temporal Attention Reweighting Algorithm (TiARA), which meticulously edits the attention score matrix based on the Discrete Short-Time Fourier Transform. Our method is supported by a theoretical guarantee, the first-of-its-kind for frequency-based methods in diffusion models. For videos generated by multiple prompts, we further investigate key factors affecting prompt interpolation quality and propose PromptBlend, an advanced prompt interpolation pipeline. The efficacy of our proposed method is validated via extensive experimental results, exhibiting consistent and impressive improvements over baseline methods. The code will be released upon acceptance.

Almost Minimax Optimal Best Arm Identification in Piecewise Stationary Linear Bandits

We propose a {\em novel} piecewise stationary linear bandit (PSLB) model, where the environment randomly samples a context from an unknown probability distribution at each changepoint, and the quality of an arm is measured by its return averaged over all contexts. The contexts and their distribution, as well as the changepoints are unknown to the agent. We design {\em Piecewise-Stationary $\varepsilon$-Best Arm Identification$^+$} (PS$\varepsilon$BAI$^+$), an algorithm that is guaranteed to identify an $\varepsilon$-optimal arm with probability $\ge 1-\delta$ and with a minimal number of samples. PS$\varepsilon$BAI$^+$ consists of two subroutines, PS$\varepsilon$BAI and {\sc Na\"ive $\varepsilon$-BAI} (N$\varepsilon$BAI), which are executed in parallel. PS$\varepsilon$BAI actively detects changepoints and aligns contexts to facilitate the arm identification process. When PS$\varepsilon$BAI and N$\varepsilon$BAI are utilized judiciously in parallel, PS$\varepsilon$BAI$^+$ is shown to have a finite expected sample complexity. By proving a lower bound, we show the expected sample complexity of PS$\varepsilon$BAI$^+$ is optimal up to a logarithmic factor. We compare PS$\varepsilon$BAI$^+$ to baseline algorithms using numerical experiments which demonstrate its efficiency. Both our analytical and numerical results corroborate that the efficacy of PS$\varepsilon$BAI$^+$ is due to the delicate change detection and context alignment procedures embedded in PS$\varepsilon$BAI.

Probably Anytime-Safe Stochastic Combinatorial Semi-Bandits

Motivated by concerns about making online decisions that incur undue amount of risk at each time step, in this paper, we formulate the probably anytime-safe stochastic combinatorial semi-bandits problem. In this problem, the agent is given the option to select a subset of size at most $K$ from a set of $L$ ground items. Each item is associated to a certain mean reward as well as a variance that represents its risk. To mitigate the risk that the agent incurs, we require that with probability at least $1-\delta$, over the entire horizon of time $T$, each of the choices that the agent makes should contain items whose sum of variances does not exceed a certain variance budget. We call this probably anytime-safe constraint. Under this constraint, we design and analyze an algorithm {\sc PASCombUCB} that minimizes the regret over the horizon of time $T$. By developing accompanying information-theoretic lower bounds, we show under both the problem-dependent and problem-independent paradigms, {\sc PASCombUCB} is almost asymptotically optimal. Our problem setup, the proposed {\sc PASCombUCB} algorithm, and novel analyses are applicable to domains such as recommendation systems and transportation in which an agent is allowed to choose multiple items at a single time step and wishes to control the risk over the whole time horizon.

Almost Optimal Variance-Constrained Best Arm Identification

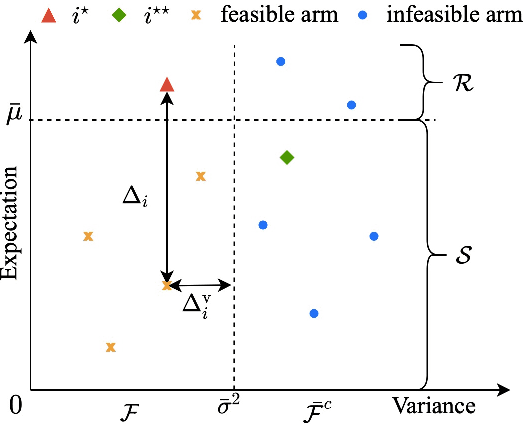
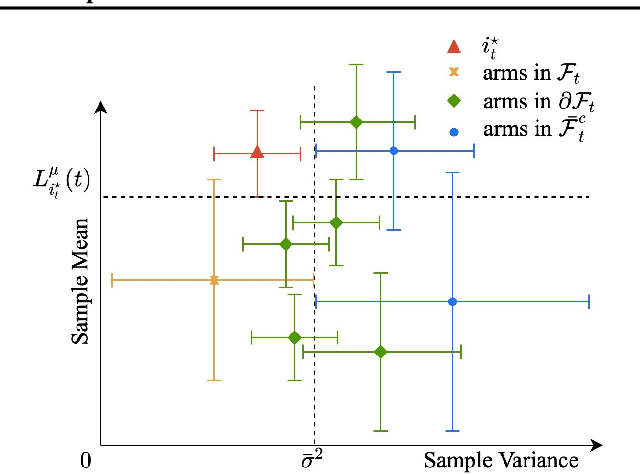
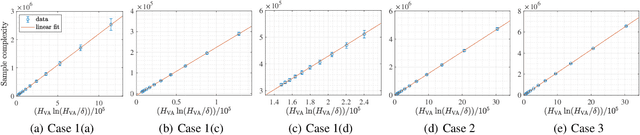
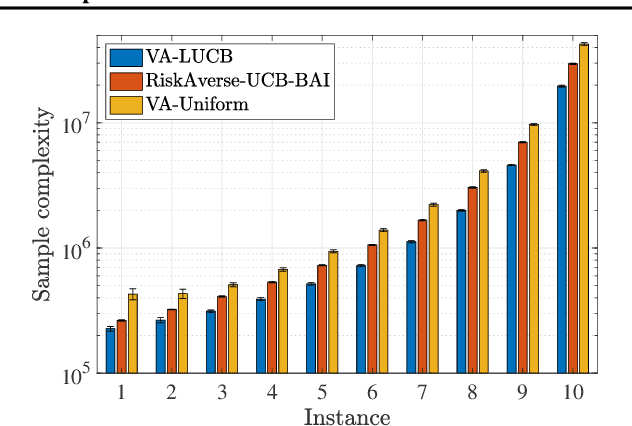
We design and analyze VA-LUCB, a parameter-free algorithm, for identifying the best arm under the fixed-confidence setup and under a stringent constraint that the variance of the chosen arm is strictly smaller than a given threshold. An upper bound on VA-LUCB's sample complexity is shown to be characterized by a fundamental variance-aware hardness quantity $H_{VA}$. By proving a lower bound, we show that sample complexity of VA-LUCB is optimal up to a factor logarithmic in $H_{VA}$. Extensive experiments corroborate the dependence of the sample complexity on the various terms in $H_{VA}$. By comparing VA-LUCB's empirical performance to a close competitor RiskAverse-UCB-BAI by David et al. (2018), our experiments suggest that VA-LUCB has the lowest sample complexity for this class of risk-constrained best arm identification problems, especially for the riskiest instances.