Sparse-to-Dense: A Free Lunch for Lossless Acceleration of Video Understanding in LLMs

Due to the auto-regressive nature of current video large language models (Video-LLMs), the inference latency increases as the input sequence length grows, posing challenges for the efficient processing of video sequences that are usually very long. We observe that during decoding, the attention scores of most tokens in Video-LLMs tend to be sparse and concentrated, with only certain tokens requiring comprehensive full attention. Based on this insight, we introduce Sparse-to-Dense (StD), a novel decoding strategy that integrates two distinct modules: one leveraging sparse top-K attention and the other employing dense full attention. These modules collaborate to accelerate Video-LLMs without loss. The fast (sparse) model speculatively decodes multiple tokens, while the slow (dense) model verifies them in parallel. StD is a tuning-free, plug-and-play solution that achieves up to a 1.94$\times$ walltime speedup in video processing. It maintains model performance while enabling a seamless transition from a standard Video-LLM to a sparse Video-LLM with minimal code modifications.

BanditSpec: Adaptive Speculative Decoding via Bandit Algorithms

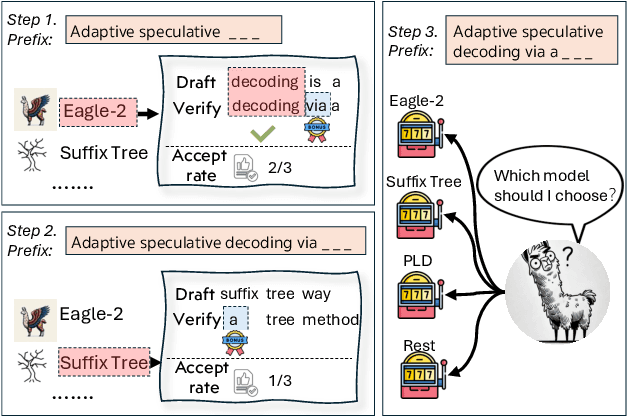
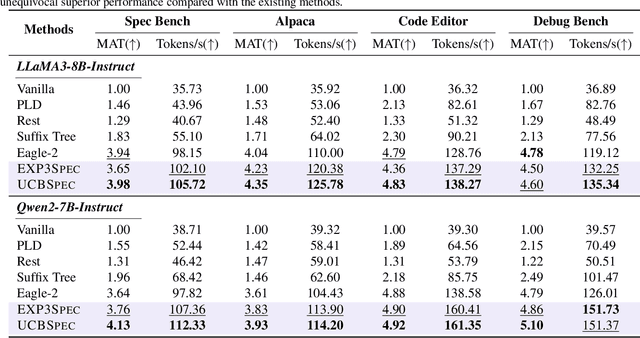
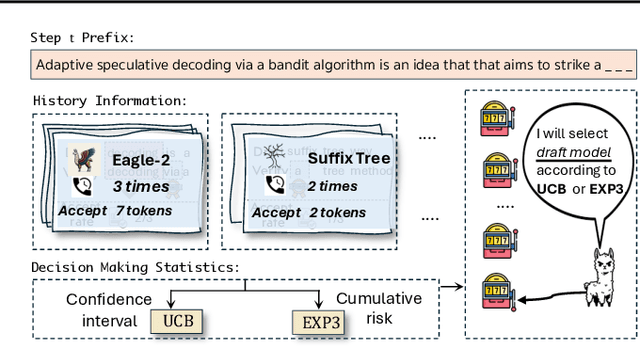
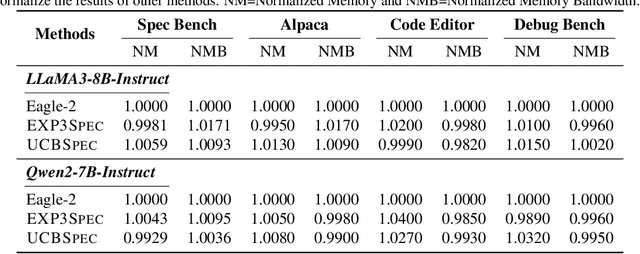
Speculative decoding has emerged as a popular method to accelerate the inference of Large Language Models (LLMs) while retaining their superior text generation performance. Previous methods either adopt a fixed speculative decoding configuration regardless of the prefix tokens, or train draft models in an offline or online manner to align them with the context. This paper proposes a training-free online learning framework to adaptively choose the configuration of the hyperparameters for speculative decoding as text is being generated. We first formulate this hyperparameter selection problem as a Multi-Armed Bandit problem and provide a general speculative decoding framework BanditSpec. Furthermore, two bandit-based hyperparameter selection algorithms, UCBSpec and EXP3Spec, are designed and analyzed in terms of a novel quantity, the stopping time regret. We upper bound this regret under both stochastic and adversarial reward settings. By deriving an information-theoretic impossibility result, it is shown that the regret performance of UCBSpec is optimal up to universal constants. Finally, extensive empirical experiments with LLaMA3 and Qwen2 demonstrate that our algorithms are effective compared to existing methods, and the throughput is close to the oracle best hyperparameter in simulated real-life LLM serving scenarios with diverse input prompts.

LongSpec: Long-Context Speculative Decoding with Efficient Drafting and Verification

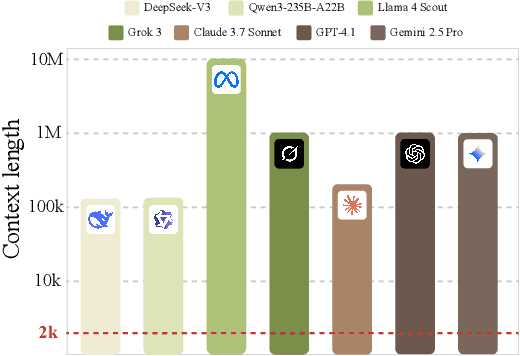
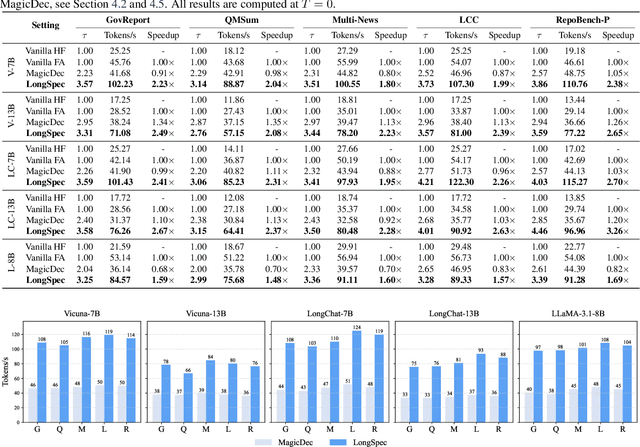
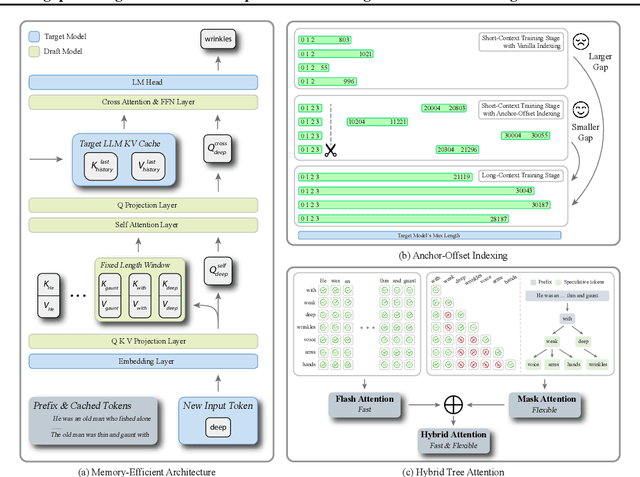
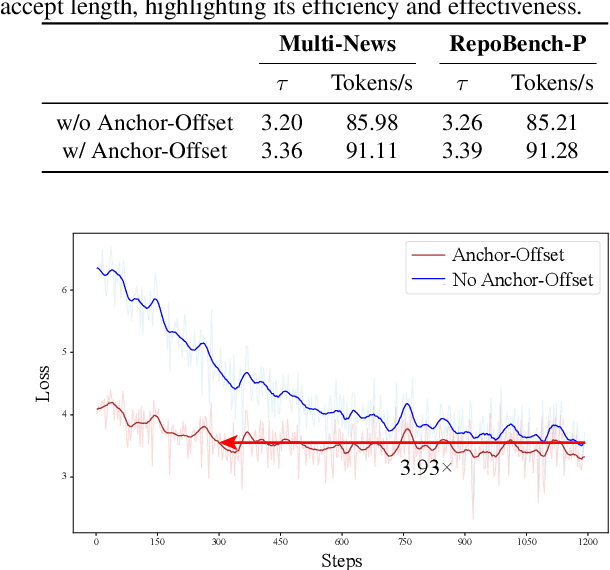
Speculative decoding has become a promising technique to mitigate the high inference latency of autoregressive decoding in Large Language Models (LLMs). Despite its promise, the effective application of speculative decoding in LLMs still confronts three key challenges: the increasing memory demands of the draft model, the distribution shift between the short-training corpora and long-context inference, and inefficiencies in attention implementation. In this work, we enhance the performance of speculative decoding in long-context settings by addressing these challenges. First, we propose a memory-efficient draft model with a constant-sized Key-Value (KV) cache. Second, we introduce novel position indices for short-training data, enabling seamless adaptation from short-context training to long-context inference. Finally, we present an innovative attention aggregation method that combines fast implementations for prefix computation with standard attention for tree mask handling, effectively resolving the latency and memory inefficiencies of tree decoding. Our approach achieves strong results on various long-context tasks, including repository-level code completion, long-context summarization, and o1-like long reasoning tasks, demonstrating significant improvements in latency reduction. The code is available at https://github.com/sail-sg/LongSpec.

Enhancing Multi-Text Long Video Generation Consistency without Tuning: Time-Frequency Analysis, Prompt Alignment, and Theory

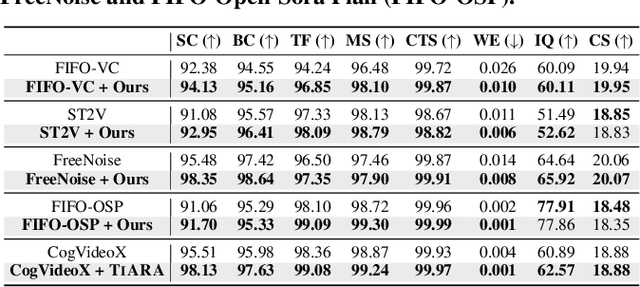
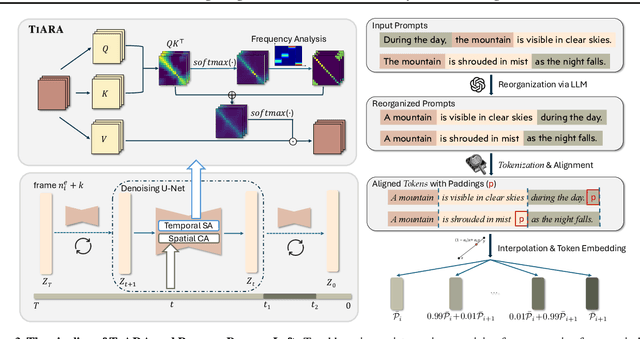
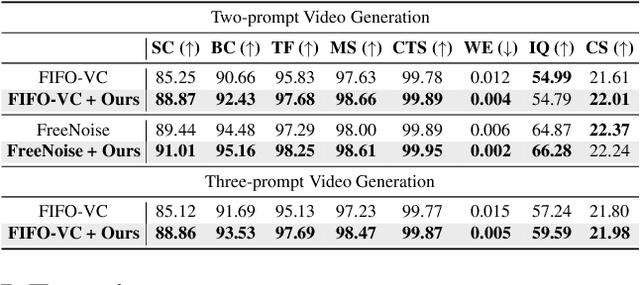
Despite the considerable progress achieved in the long video generation problem, there is still significant room to improve the consistency of the videos, particularly in terms of smoothness and transitions between scenes. We address these issues to enhance the consistency and coherence of videos generated with either single or multiple prompts. We propose the Time-frequency based temporal Attention Reweighting Algorithm (TiARA), which meticulously edits the attention score matrix based on the Discrete Short-Time Fourier Transform. Our method is supported by a theoretical guarantee, the first-of-its-kind for frequency-based methods in diffusion models. For videos generated by multiple prompts, we further investigate key factors affecting prompt interpolation quality and propose PromptBlend, an advanced prompt interpolation pipeline. The efficacy of our proposed method is validated via extensive experimental results, exhibiting consistent and impressive improvements over baseline methods. The code will be released upon acceptance.

When Attention Sink Emerges in Language Models: An Empirical View

Language Models (LMs) assign significant attention to the first token, even if it is not semantically important, which is known as attention sink. This phenomenon has been widely adopted in applications such as streaming/long context generation, KV cache optimization, inference acceleration, model quantization, and others. Despite its widespread use, a deep understanding of attention sink in LMs is still lacking. In this work, we first demonstrate that attention sinks exist universally in LMs with various inputs, even in small models. Furthermore, attention sink is observed to emerge during the LM pre-training, motivating us to investigate how optimization, data distribution, loss function, and model architecture in LM pre-training influence its emergence. We highlight that attention sink emerges after effective optimization on sufficient training data. The sink position is highly correlated with the loss function and data distribution. Most importantly, we find that attention sink acts more like key biases, storing extra attention scores, which could be non-informative and not contribute to the value computation. We also observe that this phenomenon (at least partially) stems from tokens' inner dependence on attention scores as a result of softmax normalization. After relaxing such dependence by replacing softmax attention with other attention operations, such as sigmoid attention without normalization, attention sinks do not emerge in LMs up to 1B parameters. The code is available at https://github.com/sail-sg/Attention-Sink.

Unveiling the Statistical Foundations of Chain-of-Thought Prompting Methods

Chain-of-Thought (CoT) prompting and its variants have gained popularity as effective methods for solving multi-step reasoning problems using pretrained large language models (LLMs). In this work, we analyze CoT prompting from a statistical estimation perspective, providing a comprehensive characterization of its sample complexity. To this end, we introduce a multi-step latent variable model that encapsulates the reasoning process, where the latent variable encodes the task information. Under this framework, we demonstrate that when the pretraining dataset is sufficiently large, the estimator formed by CoT prompting is equivalent to a Bayesian estimator. This estimator effectively solves the multi-step reasoning problem by aggregating a posterior distribution inferred from the demonstration examples in the prompt. Moreover, we prove that the statistical error of the CoT estimator can be decomposed into two main components: (i) a prompting error, which arises from inferring the true task using CoT prompts, and (ii) the statistical error of the pretrained LLM. We establish that, under appropriate assumptions, the prompting error decays exponentially to zero as the number of demonstrations increases. Additionally, we explicitly characterize the approximation and generalization errors of the pretrained LLM. Notably, we construct a transformer model that approximates the target distribution of the multi-step reasoning problem with an error that decreases exponentially in the number of transformer blocks. Our analysis extends to other variants of CoT, including Self-Consistent CoT, Tree-of-Thought, and Selection-Inference, offering a broad perspective on the efficacy of these methods. We also provide numerical experiments to validate the theoretical findings.

From Words to Actions: Unveiling the Theoretical Underpinnings of LLM-Driven Autonomous Systems

In this work, from a theoretical lens, we aim to understand why large language model (LLM) empowered agents are able to solve decision-making problems in the physical world. To this end, consider a hierarchical reinforcement learning (RL) model where the LLM Planner and the Actor perform high-level task planning and low-level execution, respectively. Under this model, the LLM Planner navigates a partially observable Markov decision process (POMDP) by iteratively generating language-based subgoals via prompting. Under proper assumptions on the pretraining data, we prove that the pretrained LLM Planner effectively performs Bayesian aggregated imitation learning (BAIL) through in-context learning. Additionally, we highlight the necessity for exploration beyond the subgoals derived from BAIL by proving that naively executing the subgoals returned by LLM leads to a linear regret. As a remedy, we introduce an $\epsilon$-greedy exploration strategy to BAIL, which is proven to incur sublinear regret when the pretraining error is small. Finally, we extend our theoretical framework to include scenarios where the LLM Planner serves as a world model for inferring the transition model of the environment and to multi-agent settings, enabling coordination among multiple Actors.

Learning Regularized Graphon Mean-Field Games with Unknown Graphons

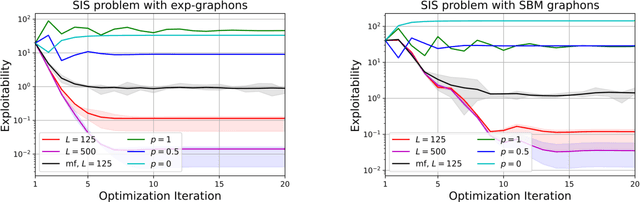
We design and analyze reinforcement learning algorithms for Graphon Mean-Field Games (GMFGs). In contrast to previous works that require the precise values of the graphons, we aim to learn the Nash Equilibrium (NE) of the regularized GMFGs when the graphons are unknown. Our contributions are threefold. First, we propose the Proximal Policy Optimization for GMFG (GMFG-PPO) algorithm and show that it converges at a rate of $O(T^{-1/3})$ after $T$ iterations with an estimation oracle, improving on a previous work by Xie et al. (ICML, 2021). Second, using kernel embedding of distributions, we design efficient algorithms to estimate the transition kernels, reward functions, and graphons from sampled agents. Convergence rates are then derived when the positions of the agents are either known or unknown. Results for the combination of the optimization algorithm GMFG-PPO and the estimation algorithm are then provided. These algorithms are the first specifically designed for learning graphons from sampled agents. Finally, the efficacy of the proposed algorithms are corroborated through simulations. These simulations demonstrate that learning the unknown graphons reduces the exploitability effectively.

Learning Regularized Monotone Graphon Mean-Field Games

This paper studies two fundamental problems in regularized Graphon Mean-Field Games (GMFGs). First, we establish the existence of a Nash Equilibrium (NE) of any $\lambda$-regularized GMFG (for $\lambda\geq 0$). This result relies on weaker conditions than those in previous works for analyzing both unregularized GMFGs ($\lambda=0$) and $\lambda$-regularized MFGs, which are special cases of GMFGs. Second, we propose provably efficient algorithms to learn the NE in weakly monotone GMFGs, motivated by Lasry and Lions [2007]. Previous literature either only analyzed continuous-time algorithms or required extra conditions to analyze discrete-time algorithms. In contrast, we design a discrete-time algorithm and derive its convergence rate solely under weakly monotone conditions. Furthermore, we develop and analyze the action-value function estimation procedure during the online learning process, which is absent from algorithms for monotone GMFGs. This serves as a sub-module in our optimization algorithm. The efficiency of the designed algorithm is corroborated by empirical evaluations.

What and How does In-Context Learning Learn? Bayesian Model Averaging, Parameterization, and Generalization

In this paper, we conduct a comprehensive study of In-Context Learning (ICL) by addressing several open questions: (a) What type of ICL estimator is learned within language models? (b) What are suitable performance metrics to evaluate ICL accurately and what are the error rates? (c) How does the transformer architecture enable ICL? To answer (a), we take a Bayesian view and demonstrate that ICL implicitly implements the Bayesian model averaging algorithm. This Bayesian model averaging algorithm is proven to be approximately parameterized by the attention mechanism. For (b), we analyze the ICL performance from an online learning perspective and establish a regret bound $\mathcal{O}(1/T)$, where $T$ is the ICL input sequence length. To address (c), in addition to the encoded Bayesian model averaging algorithm in attention, we show that during pertaining, the total variation distance between the learned model and the nominal model is bounded by a sum of an approximation error and a generalization error of $\tilde{\mathcal{O}}(1/\sqrt{N_{\mathrm{p}}T_{\mathrm{p}}})$, where $N_{\mathrm{p}}$ and $T_{\mathrm{p}}$ are the number of token sequences and the length of each sequence in pretraining, respectively. Our results provide a unified understanding of the transformer and its ICL ability with bounds on ICL regret, approximation, and generalization, which deepens our knowledge of these essential aspects of modern language models.