Speeding-up Symbol-Level Precoding Using Separable and Dual Optimizations
Paper and Code
Nov 27, 2022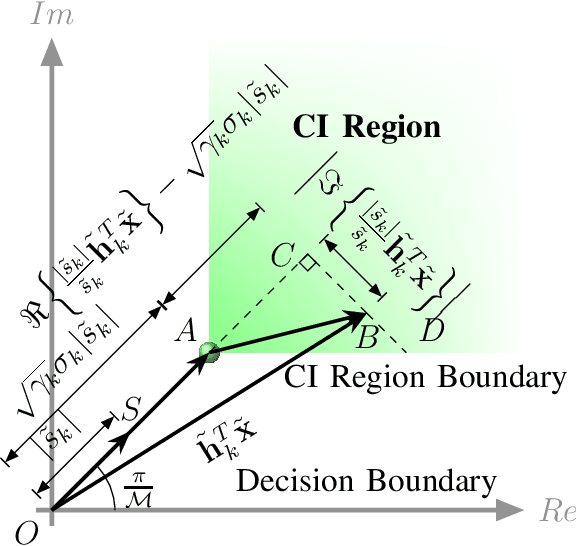
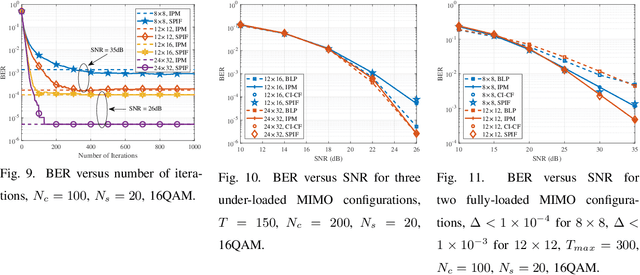
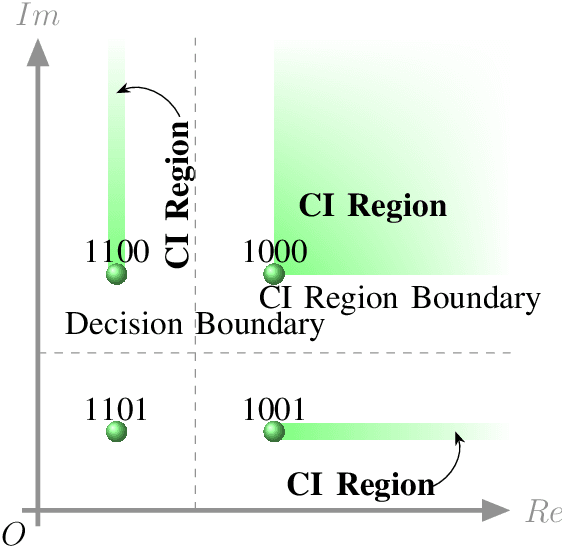
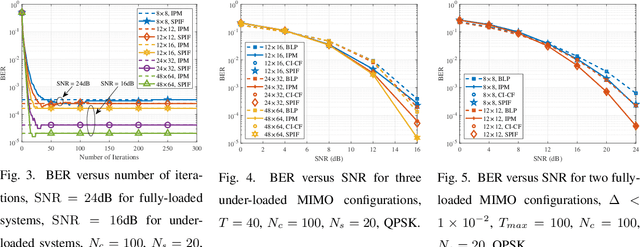
Symbol-level precoding (SLP) manipulates the transmitted signals to accurately exploit the multi-user interference (MUI) in the multi-user downlink. This enables that all the resultant interference contributes to correct detection, which is the so-called constructive interference (CI). Its performance superiority comes at the cost of solving a nonlinear optimization problem on a symbol-by-symbol basis, for which the resulting complexity becomes prohibitive in realistic wireless communication systems. In this paper, we investigate low-complexity SLP algorithms for both phase-shift keying (PSK) and quadrature amplitude modulation (QAM). Specifically, we first prove that the max-min SINR balancing (SB) SLP problem for PSK signaling is not separable, which is contrary to the power minimization (PM) SLP problem, and accordingly, existing decomposition methods are not applicable. Next, we establish an explicit duality between the PM-SLP and SB-SLP problems for PSK modulation. The proposed duality facilitates obtaining the solution to the SB-SLP given the solution to the PM-SLP without the need for one-dimension search, and vice versa. We then propose a closed-form power scaling algorithm to solve the SB-SLP via PM-SLP to take advantage of the separability of the PM-SLP. As for QAM modulation, we convert the PM-SLP problem into a separable equivalent optimization problem, and decompose the new problem into several simple parallel subproblems with closed-form solutions, leveraging the proximal Jacobian alternating direction method of multipliers (PJ-ADMM). We further prove that the proposed duality can be generalized to the multi-level modulation case, based on which a power scaling parallel inverse-free algorithm is also proposed to solve the SB-SLP for QAM signaling. Numerical results show that the proposed algorithms offer optimal performance with lower complexity than the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge