POLCA: Stochastic Generative Optimization with LLM

Optimizing complex systems, ranging from LLM prompts to multi-turn agents, traditionally requires labor-intensive manual iteration. We formalize this challenge as a stochastic generative optimization problem where a generative language model acts as the optimizer, guided by numerical rewards and text feedback to discover the best system. We introduce Prioritized Optimization with Local Contextual Aggregation (POLCA), a scalable framework designed to handle stochasticity in optimization -- such as noisy feedback, sampling minibatches, and stochastic system behaviors -- while effectively managing the unconstrained expansion of solution space. POLCA maintains a priority queue to manage the exploration-exploitation tradeoff, systematically tracking candidate solutions and their evaluation histories. To enhance efficiency, we integrate an $\varepsilon$-Net mechanism to maintain parameter diversity and an LLM Summarizer to perform meta-learning across historical trials. We theoretically prove that POLCA converges to near-optimal candidate solutions under stochasticity. We evaluate our framework on diverse benchmarks, including $τ$-bench, HotpotQA (agent optimization), VeriBench (code translation) and KernelBench (CUDA kernel generation). Experimental results demonstrate that POLCA achieves robust, sample and time-efficient performance, consistently outperforming state-of-the-art algorithms in both deterministic and stochastic problems. The codebase for this work is publicly available at https://github.com/rlx-lab/POLCA.

Optimal Batched Linear Bandits

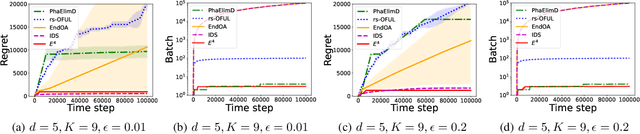
We introduce the E$^4$ algorithm for the batched linear bandit problem, incorporating an Explore-Estimate-Eliminate-Exploit framework. With a proper choice of exploration rate, we prove E$^4$ achieves the finite-time minimax optimal regret with only $O(\log\log T)$ batches, and the asymptotically optimal regret with only $3$ batches as $T\rightarrow\infty$, where $T$ is the time horizon. We further prove a lower bound on the batch complexity of linear contextual bandits showing that any asymptotically optimal algorithm must require at least $3$ batches in expectation as $T\rightarrow\infty$, which indicates E$^4$ achieves the asymptotic optimality in regret and batch complexity simultaneously. To the best of our knowledge, E$^4$ is the first algorithm for linear bandits that simultaneously achieves the minimax and asymptotic optimality in regret with the corresponding optimal batch complexities. In addition, we show that with another choice of exploration rate E$^4$ achieves an instance-dependent regret bound requiring at most $O(\log T)$ batches, and maintains the minimax optimality and asymptotic optimality. We conduct thorough experiments to evaluate our algorithm on randomly generated instances and the challenging \textit{End of Optimism} instances \citep{lattimore2017end} which were shown to be hard to learn for optimism based algorithms. Empirical results show that E$^4$ consistently outperforms baseline algorithms with respect to regret minimization, batch complexity, and computational efficiency.