How to Provably Improve Return Conditioned Supervised Learning?

In sequential decision-making problems, Return-Conditioned Supervised Learning (RCSL) has gained increasing recognition for its simplicity and stability in modern decision-making tasks. Unlike traditional offline reinforcement learning (RL) algorithms, RCSL frames policy learning as a supervised learning problem by taking both the state and return as input. This approach eliminates the instability often associated with temporal difference (TD) learning in offline RL. However, RCSL has been criticized for lacking the stitching property, meaning its performance is inherently limited by the quality of the policy used to generate the offline dataset. To address this limitation, we propose a principled and simple framework called Reinforced RCSL. The key innovation of our framework is the introduction of a concept we call the in-distribution optimal return-to-go. This mechanism leverages our policy to identify the best achievable in-dataset future return based on the current state, avoiding the need for complex return augmentation techniques. Our theoretical analysis demonstrates that Reinforced RCSL can consistently outperform the standard RCSL approach. Empirical results further validate our claims, showing significant performance improvements across a range of benchmarks.

Linear Mixture Distributionally Robust Markov Decision Processes

Many real-world decision-making problems face the off-dynamics challenge: the agent learns a policy in a source domain and deploys it in a target domain with different state transitions. The distributionally robust Markov decision process (DRMDP) addresses this challenge by finding a robust policy that performs well under the worst-case environment within a pre-specified uncertainty set of transition dynamics. Its effectiveness heavily hinges on the proper design of these uncertainty sets, based on prior knowledge of the dynamics. In this work, we propose a novel linear mixture DRMDP framework, where the nominal dynamics is assumed to be a linear mixture model. In contrast with existing uncertainty sets directly defined as a ball centered around the nominal kernel, linear mixture DRMDPs define the uncertainty sets based on a ball around the mixture weighting parameter. We show that this new framework provides a more refined representation of uncertainties compared to conventional models based on $(s,a)$-rectangularity and $d$-rectangularity, when prior knowledge about the mixture model is present. We propose a meta algorithm for robust policy learning in linear mixture DRMDPs with general $f$-divergence defined uncertainty sets, and analyze its sample complexities under three divergence metrics instantiations: total variation, Kullback-Leibler, and $\chi^2$ divergences. These results establish the statistical learnability of linear mixture DRMDPs, laying the theoretical foundation for future research on this new setting.

Return Augmented Decision Transformer for Off-Dynamics Reinforcement Learning

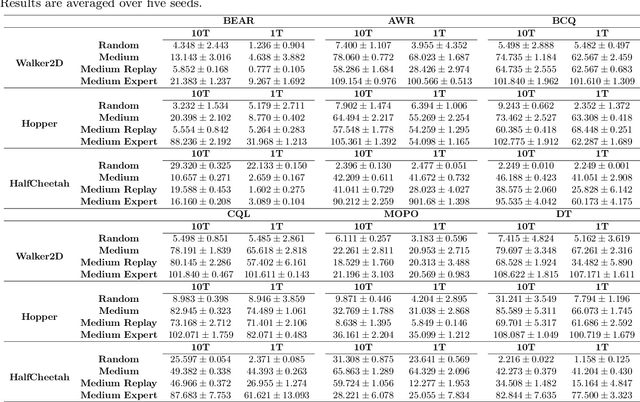
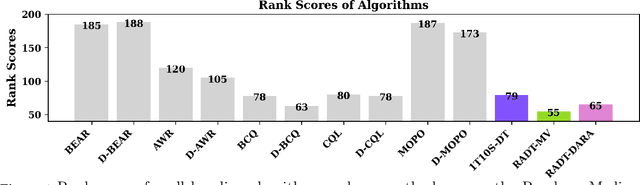
We study offline off-dynamics reinforcement learning (RL) to utilize data from an easily accessible source domain to enhance policy learning in a target domain with limited data. Our approach centers on return-conditioned supervised learning (RCSL), particularly focusing on the decision transformer (DT), which can predict actions conditioned on desired return guidance and complete trajectory history. Previous works tackle the dynamics shift problem by augmenting the reward in the trajectory from the source domain to match the optimal trajectory in the target domain. However, this strategy can not be directly applicable in RCSL owing to (1) the unique form of the RCSL policy class, which explicitly depends on the return, and (2) the absence of a straightforward representation of the optimal trajectory distribution. We propose the Return Augmented Decision Transformer (RADT) method, where we augment the return in the source domain by aligning its distribution with that in the target domain. We provide the theoretical analysis demonstrating that the RCSL policy learned from RADT achieves the same level of suboptimality as would be obtained without a dynamics shift. We introduce two practical implementations RADT-DARA and RADT-MV respectively. Extensive experiments conducted on D4RL datasets reveal that our methods generally outperform dynamic programming based methods in off-dynamics RL scenarios.

Upper and Lower Bounds for Distributionally Robust Off-Dynamics Reinforcement Learning

We study off-dynamics Reinforcement Learning (RL), where the policy training and deployment environments are different. To deal with this environmental perturbation, we focus on learning policies robust to uncertainties in transition dynamics under the framework of distributionally robust Markov decision processes (DRMDPs), where the nominal and perturbed dynamics are linear Markov Decision Processes. We propose a novel algorithm We-DRIVE-U that enjoys an average suboptimality $\widetilde{\mathcal{O}}\big({d H \cdot \min \{1/{\rho}, H\}/\sqrt{K} }\big)$, where $K$ is the number of episodes, $H$ is the horizon length, $d$ is the feature dimension and $\rho$ is the uncertainty level. This result improves the state-of-the-art by $\mathcal{O}(dH/\min\{1/\rho,H\})$. We also construct a novel hard instance and derive the first information-theoretic lower bound in this setting, which indicates our algorithm is near-optimal up to $\mathcal{O}(\sqrt{H})$ for any uncertainty level $\rho\in(0,1]$. Our algorithm also enjoys a 'rare-switching' design, and thus only requires $\mathcal{O}(dH\log(1+H^2K))$ policy switches and $\mathcal{O}(d^2H\log(1+H^2K))$ calls for oracle to solve dual optimization problems, which significantly improves the computational efficiency of existing algorithms for DRMDPs, whose policy switch and oracle complexities are both $\mathcal{O}(K)$.

Minimax Optimal and Computationally Efficient Algorithms for Distributionally Robust Offline Reinforcement Learning

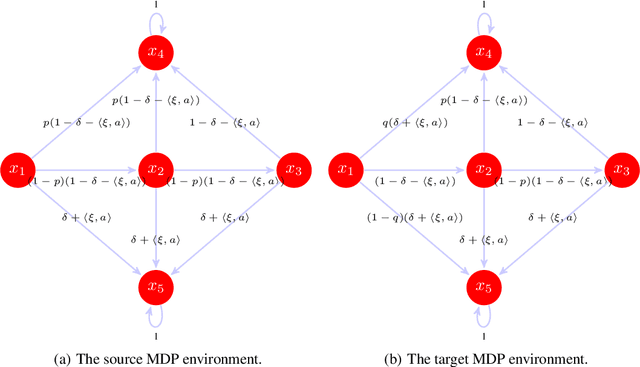
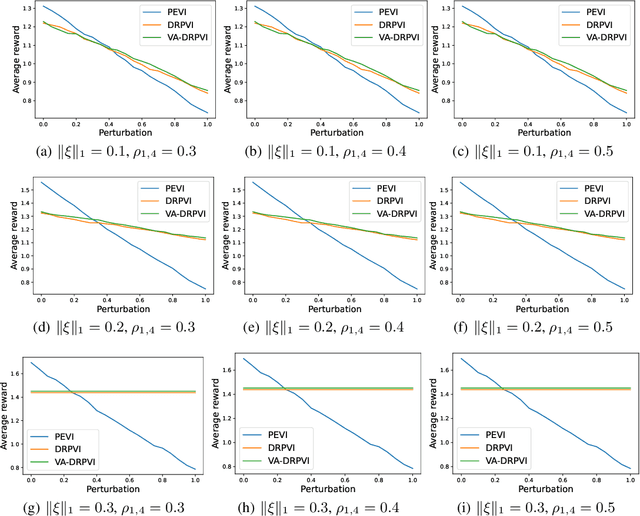
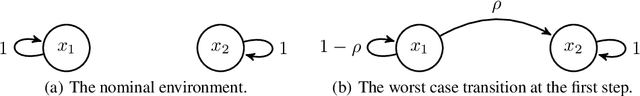
Distributionally robust offline reinforcement learning (RL), which seeks robust policy training against environment perturbation by modeling dynamics uncertainty, calls for function approximations when facing large state-action spaces. However, the consideration of dynamics uncertainty introduces essential nonlinearity and computational burden, posing unique challenges for analyzing and practically employing function approximation. Focusing on a basic setting where the nominal model and perturbed models are linearly parameterized, we propose minimax optimal and computationally efficient algorithms realizing function approximation and initiate the study on instance-dependent suboptimality analysis in the context of robust offline RL. Our results uncover that function approximation in robust offline RL is essentially distinct from and probably harder than that in standard offline RL. Our algorithms and theoretical results crucially depend on a variety of new techniques, involving a novel function approximation mechanism incorporating variance information, a new procedure of suboptimality and estimation uncertainty decomposition, a quantification of the robust value function shrinkage, and a meticulously designed family of hard instances, which might be of independent interest.

Distributionally Robust Off-Dynamics Reinforcement Learning: Provable Efficiency with Linear Function Approximation

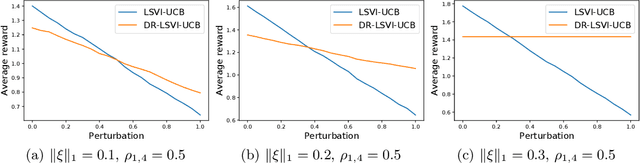
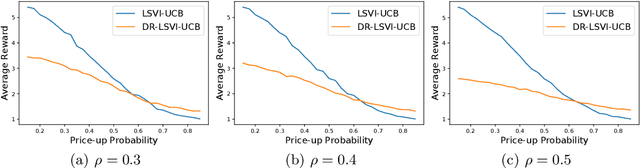
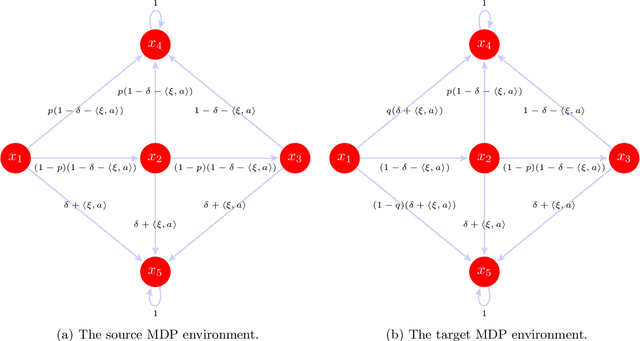
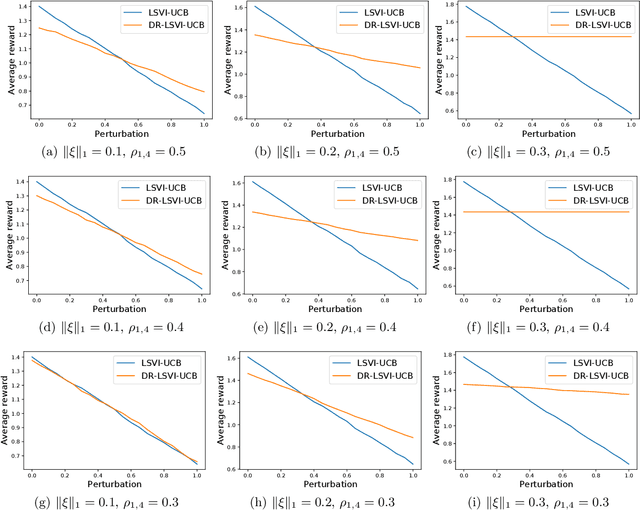
We study off-dynamics Reinforcement Learning (RL), where the policy is trained on a source domain and deployed to a distinct target domain. We aim to solve this problem via online distributionally robust Markov decision processes (DRMDPs), where the learning algorithm actively interacts with the source domain while seeking the optimal performance under the worst possible dynamics that is within an uncertainty set of the source domain's transition kernel. We provide the first study on online DRMDPs with function approximation for off-dynamics RL. We find that DRMDPs' dual formulation can induce nonlinearity, even when the nominal transition kernel is linear, leading to error propagation. By designing a $d$-rectangular uncertainty set using the total variation distance, we remove this additional nonlinearity and bypass the error propagation. We then introduce DR-LSVI-UCB, the first provably efficient online DRMDP algorithm for off-dynamics RL with function approximation, and establish a polynomial suboptimality bound that is independent of the state and action space sizes. Our work makes the first step towards a deeper understanding of the provable efficiency of online DRMDPs with linear function approximation. Finally, we substantiate the performance and robustness of DR-LSVI-UCB through different numerical experiments.

Convergence of Sign-based Random Reshuffling Algorithms for Nonconvex Optimization

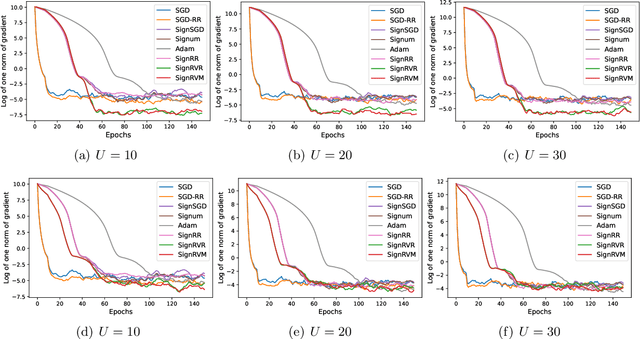
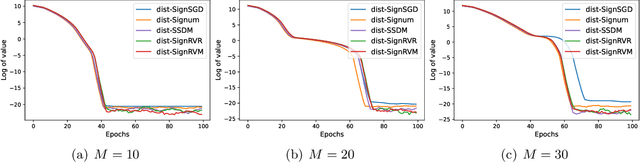
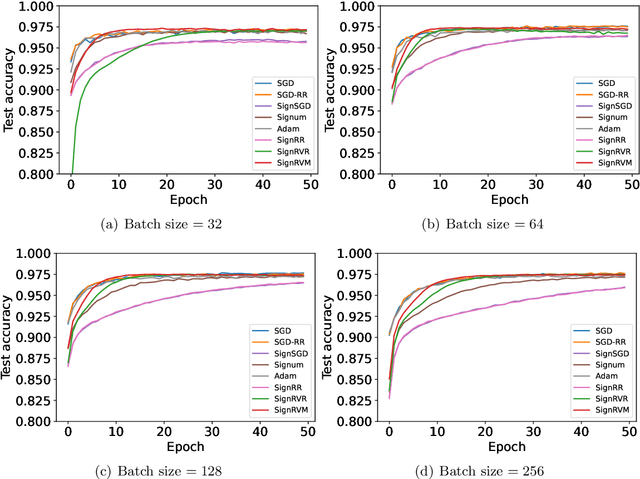
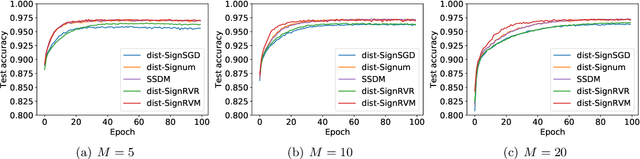
signSGD is popular in nonconvex optimization due to its communication efficiency. Yet, existing analyses of signSGD rely on assuming that data are sampled with replacement in each iteration, contradicting the practical implementation where data are randomly reshuffled and sequentially fed into the algorithm. We bridge this gap by proving the first convergence result of signSGD with random reshuffling (SignRR) for nonconvex optimization. Given the dataset size $n$, the number of epochs of data passes $T$, and the variance bound of a stochastic gradient $\sigma^2$, we show that SignRR has the same convergence rate $O(\log(nT)/\sqrt{nT} + \|\sigma\|_1)$ as signSGD \citep{bernstein2018signsgd}. We then present SignRVR and SignRVM, which leverage variance-reduced gradients and momentum updates respectively, both converging at $O(\log(nT)/\sqrt{nT})$. In contrast with the analysis of signSGD, our results do not require an extremely large batch size in each iteration to be of the same order as the total number of iterations \citep{bernstein2018signsgd} or the signs of stochastic and true gradients match element-wise with a minimum probability of 1/2 \citep{safaryan2021stochastic}. We also extend our algorithms to cases where data are distributed across different machines, yielding dist-SignRVR and dist-SignRVM, both converging at $O(\log(n_0T)/\sqrt{n_0T})$, where $n_0$ is the dataset size of a single machine. We back up our theoretical findings through experiments on simulated and real-world problems, verifying that randomly reshuffled sign methods match or surpass existing baselines.