Minimax Optimal and Computationally Efficient Algorithms for Distributionally Robust Offline Reinforcement Learning
Paper and Code
Mar 14, 2024
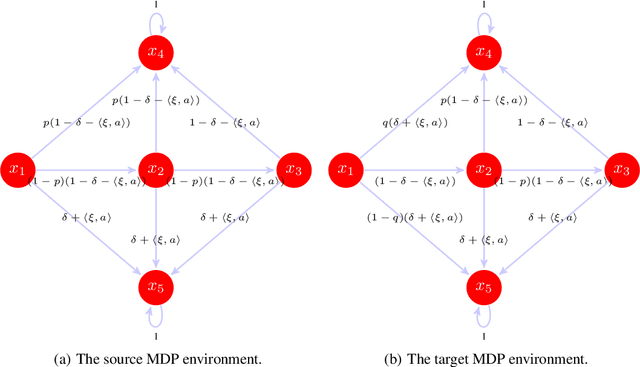
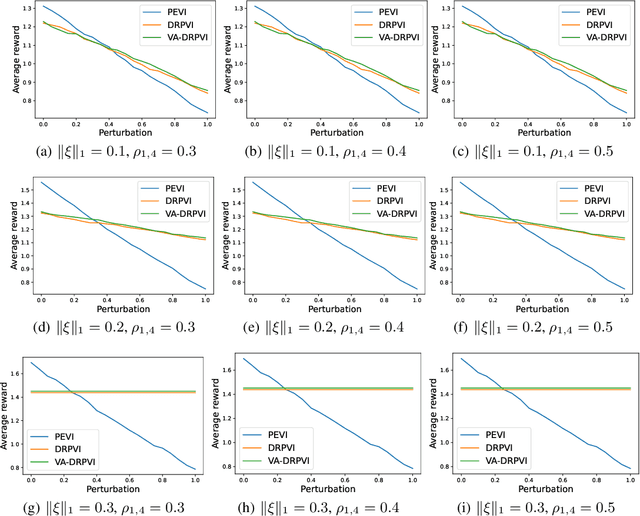
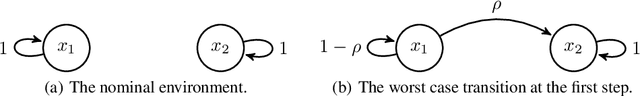
Distributionally robust offline reinforcement learning (RL), which seeks robust policy training against environment perturbation by modeling dynamics uncertainty, calls for function approximations when facing large state-action spaces. However, the consideration of dynamics uncertainty introduces essential nonlinearity and computational burden, posing unique challenges for analyzing and practically employing function approximation. Focusing on a basic setting where the nominal model and perturbed models are linearly parameterized, we propose minimax optimal and computationally efficient algorithms realizing function approximation and initiate the study on instance-dependent suboptimality analysis in the context of robust offline RL. Our results uncover that function approximation in robust offline RL is essentially distinct from and probably harder than that in standard offline RL. Our algorithms and theoretical results crucially depend on a variety of new techniques, involving a novel function approximation mechanism incorporating variance information, a new procedure of suboptimality and estimation uncertainty decomposition, a quantification of the robust value function shrinkage, and a meticulously designed family of hard instances, which might be of independent interest.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge