Zhen Qin
Reinforcement Fine-Tuning for History-Aware Dense Retriever in RAG
Feb 03, 2026Abstract:Retrieval-augmented generation (RAG) enables large language models (LLMs) to produce evidence-based responses, and its performance hinges on the matching between the retriever and LLMs. Retriever optimization has emerged as an efficient alternative to fine-tuning LLMs. However, existing solutions suffer from objective mismatch between retriever optimization and the goal of RAG pipeline. Reinforcement learning (RL) provides a promising solution to address this limitation, yet applying RL to retriever optimization introduces two fundamental challenges: 1) the deterministic retrieval is incompatible with RL formulations, and 2) state aliasing arises from query-only retrieval in multi-hop reasoning. To address these challenges, we replace deterministic retrieval with stochastic sampling and formulate RAG as a Markov decision process, making retriever optimizable by RL. Further, we incorporate retrieval history into the state at each retrieval step to mitigate state aliasing. Extensive experiments across diverse RAG pipelines, datasets, and retriever scales demonstrate consistent improvements of our approach in RAG performance.
Adaptive Dual-Weighting Framework for Federated Learning via Out-of-Distribution Detection
Feb 01, 2026Abstract:Federated Learning (FL) enables collaborative model training across large-scale distributed service nodes while preserving data privacy, making it a cornerstone of intelligent service systems in edge-cloud environments. However, in real-world service-oriented deployments, data generated by heterogeneous users, devices, and application scenarios are inherently non-IID. This severe data heterogeneity critically undermines the convergence stability, generalization ability, and ultimately the quality of service delivered by the global model. To address this challenge, we propose FLood, a novel FL framework inspired by out-of-distribution (OOD) detection. FLood dynamically counteracts the adverse effects of heterogeneity through a dual-weighting mechanism that jointly governs local training and global aggregation. At the client level, it adaptively reweights the supervised loss by upweighting pseudo-OOD samples, thereby encouraging more robust learning from distributionally misaligned or challenging data. At the server level, it refines model aggregation by weighting client contributions according to their OOD confidence scores, prioritizing updates from clients with higher in-distribution consistency and enhancing the global model's robustness and convergence stability. Extensive experiments across multiple benchmarks under diverse non-IID settings demonstrate that FLood consistently outperforms state-of-the-art FL methods in both accuracy and generalization. Furthermore, FLood functions as an orthogonal plug-in module: it seamlessly integrates with existing FL algorithms to boost their performance under heterogeneity without modifying their core optimization logic. These properties make FLood a practical and scalable solution for deploying reliable intelligent services in real-world federated environments.
Can Vision-Language Models Handle Long-Context Code? An Empirical Study on Visual Compression
Jan 31, 2026Abstract:Large Language Models (LLMs) struggle with long-context code due to window limitations. Existing textual code compression methods mitigate this via selective filtering but often disrupt dependency closure, causing semantic fragmentation. To address this, we introduce LongCodeOCR, a visual compression framework that renders code into compressed two-dimensional image sequences for Vision-Language Models (VLMs). By preserving a global view, this approach avoids the dependency breakage inherent in filtering. We systematically evaluate LongCodeOCR against the state-of-the-art LongCodeZip across four benchmarks spanning code summarization, code question answering, and code completion. Our results demonstrate that visual code compression serves as a viable alternative for tasks requiring global understanding. At comparable compression ratios ($\sim$1.7$\times$), LongCodeOCR improves CompScore on Long Module Summarization by 36.85 points over LongCodeZip. At a 1M-token context length with Glyph (a specialized 9B VLM), LongCodeOCR maintains higher accuracy than LongCodeZip while operating at about 4$\times$ higher compression. Moreover, compared with LongCodeZip, LongCodeOCR drastically reduces compression-stage overhead (reducing latency from $\sim$4.3 hours to $\sim$1 minute at 1M tokens). Finally, our results characterize a fundamental coverage--fidelity trade-off: visual code compression retains broader context coverage to support global dependencies, yet faces fidelity bottlenecks on exactness-critical tasks; by contrast, textual code compression preserves symbol-level precision while sacrificing structural coverage.
Group Representational Position Encoding
Dec 08, 2025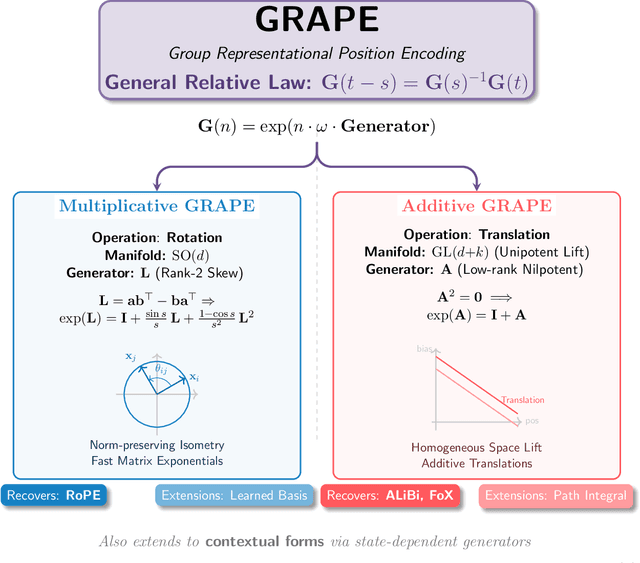
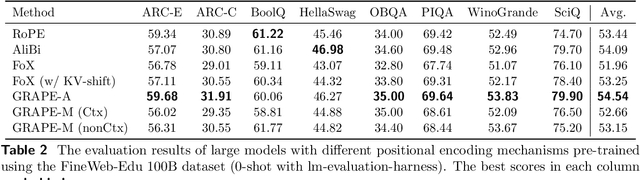
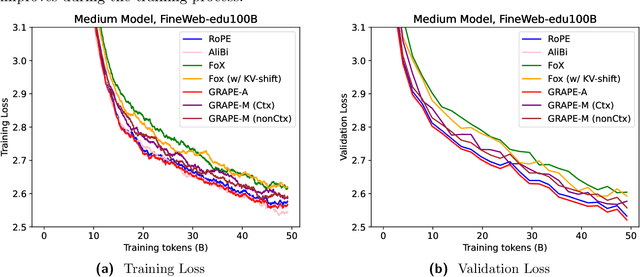

Abstract:We present GRAPE (Group RepresentAtional Position Encoding), a unified framework for positional encoding based on group actions. GRAPE brings together two families of mechanisms: (i) multiplicative rotations (Multiplicative GRAPE) in $\mathrm{SO}(d)$ and (ii) additive logit biases (Additive GRAPE) arising from unipotent actions in the general linear group $\mathrm{GL}$. In Multiplicative GRAPE, a position $n \in \mathbb{Z}$ (or $t \in \mathbb{R}$) acts as $\mathbf{G}(n)=\exp(n\,ω\,\mathbf{L})$ with a rank-2 skew generator $\mathbf{L} \in \mathbb{R}^{d \times d}$, yielding a relative, compositional, norm-preserving map with a closed-form matrix exponential. RoPE is recovered exactly when the $d/2$ planes are the canonical coordinate pairs with log-uniform spectrum. Learned commuting subspaces and compact non-commuting mixtures strictly extend this geometry to capture cross-subspace feature coupling at $O(d)$ and $O(r d)$ cost per head, respectively. In Additive GRAPE, additive logits arise as rank-1 (or low-rank) unipotent actions, recovering ALiBi and the Forgetting Transformer (FoX) as exact special cases while preserving an exact relative law and streaming cacheability. Altogether, GRAPE supplies a principled design space for positional geometry in long-context models, subsuming RoPE and ALiBi as special cases. Project Page: https://github.com/model-architectures/GRAPE.
Higher-order Linear Attention
Oct 31, 2025Abstract:The quadratic cost of scaled dot-product attention is a central obstacle to scaling autoregressive language models to long contexts. Linear-time attention and State Space Models (SSMs) provide scalable alternatives but are typically restricted to first-order or kernel-based approximations, which can limit expressivity. We introduce Higher-order Linear Attention (HLA), a causal, streaming mechanism that realizes higher interactions via compact prefix sufficient statistics. In the second-order case, HLA maintains a constant-size state and computes per-token outputs in linear time without materializing any $n \times n$ matrices. We give closed-form streaming identities, a strictly causal masked variant using two additional summaries, and a chunk-parallel training scheme based on associative scans that reproduces the activations of a serial recurrence exactly. We further outline extensions to third and higher orders. Collectively, these results position HLA as a principled, scalable building block that combines attention-like, data-dependent mixing with the efficiency of modern recurrent architectures. Project Page: https://github.com/yifanzhang-pro/HLA.
Elucidating the Design Space of Decay in Linear Attention
Sep 05, 2025Abstract:This paper presents a comprehensive investigation into the decay mechanisms inherent in linear complexity sequence models. We systematically delineate the design space of decay mechanisms across four pivotal dimensions: parameterization strategy, which refers to the computational methodology for decay; parameter sharing, which involves the utilization of supplementary parameters for decay computation; decay granularity, comparing scalar versus vector-based decay; and compatibility with relative positional encoding methods, such as Rotary Position Embedding (RoPE). Through an extensive series of experiments conducted on diverse language modeling tasks, we uncovered several critical insights. Firstly, the design of the parameterization strategy for decay requires meticulous consideration. Our findings indicate that effective configurations are typically confined to a specific range of parameters. Secondly, parameter sharing cannot be used arbitrarily, as it may cause decay values to be too large or too small, thereby significantly impacting performance. Thirdly, under identical parameterization strategies, scalar decay generally underperforms compared to its vector-based counterpart. However, in certain scenarios with alternative parameterization strategies, scalar decay may unexpectedly surpass vector decay in efficacy. Lastly, our analysis reveals that RoPE, a commonly employed relative positional encoding method, typically fails to provide tangible benefits to the majority of linear attention mechanisms.
AlphaGo Moment for Model Architecture Discovery
Jul 24, 2025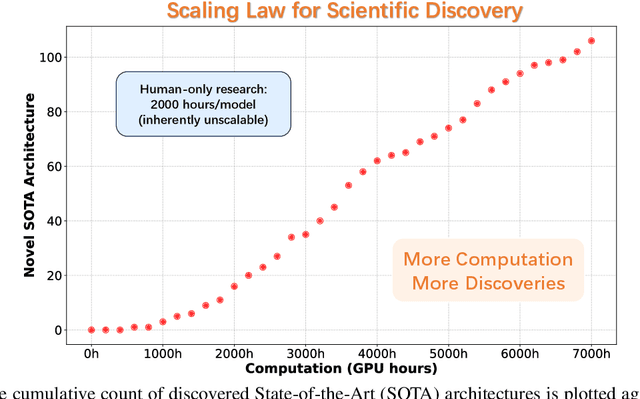
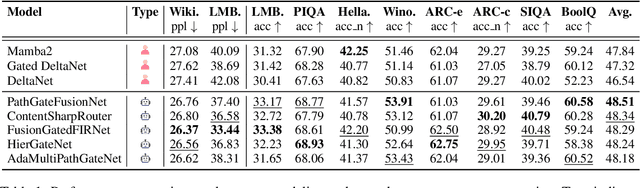
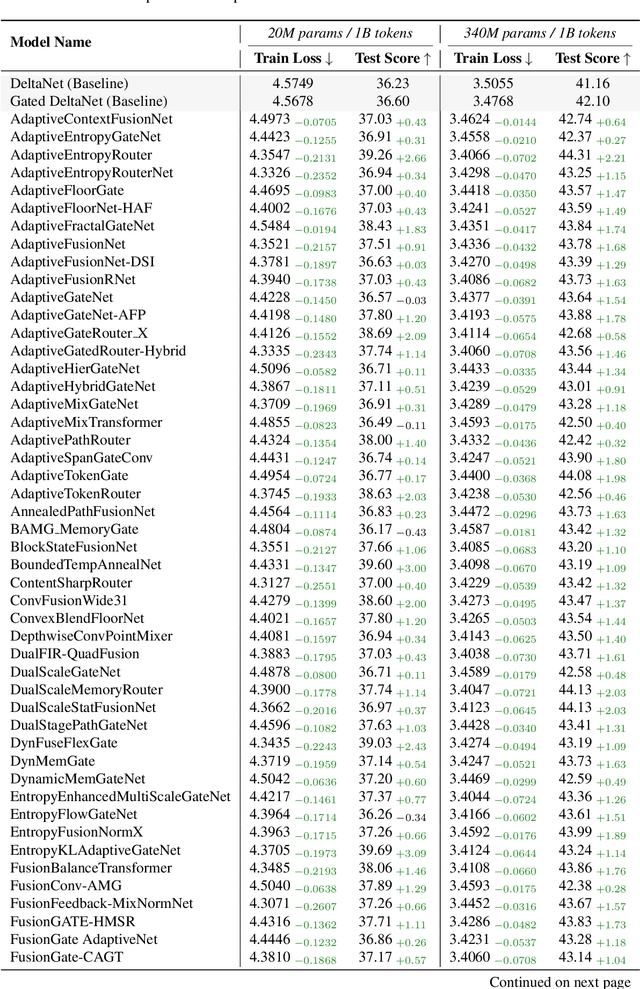
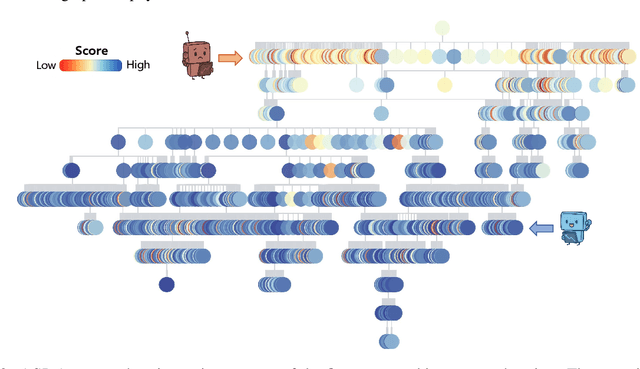
Abstract:While AI systems demonstrate exponentially improving capabilities, the pace of AI research itself remains linearly bounded by human cognitive capacity, creating an increasingly severe development bottleneck. We present ASI-Arch, the first demonstration of Artificial Superintelligence for AI research (ASI4AI) in the critical domain of neural architecture discovery--a fully autonomous system that shatters this fundamental constraint by enabling AI to conduct its own architectural innovation. Moving beyond traditional Neural Architecture Search (NAS), which is fundamentally limited to exploring human-defined spaces, we introduce a paradigm shift from automated optimization to automated innovation. ASI-Arch can conduct end-to-end scientific research in the domain of architecture discovery, autonomously hypothesizing novel architectural concepts, implementing them as executable code, training and empirically validating their performance through rigorous experimentation and past experience. ASI-Arch conducted 1,773 autonomous experiments over 20,000 GPU hours, culminating in the discovery of 106 innovative, state-of-the-art (SOTA) linear attention architectures. Like AlphaGo's Move 37 that revealed unexpected strategic insights invisible to human players, our AI-discovered architectures demonstrate emergent design principles that systematically surpass human-designed baselines and illuminate previously unknown pathways for architectural innovation. Crucially, we establish the first empirical scaling law for scientific discovery itself--demonstrating that architectural breakthroughs can be scaled computationally, transforming research progress from a human-limited to a computation-scalable process. We provide comprehensive analysis of the emergent design patterns and autonomous research capabilities that enabled these breakthroughs, establishing a blueprint for self-accelerating AI systems.
Autoregressive Image Generation with Linear Complexity: A Spatial-Aware Decay Perspective
Jul 02, 2025Abstract:Autoregressive (AR) models have garnered significant attention in image generation for their ability to effectively capture both local and global structures within visual data. However, prevalent AR models predominantly rely on the transformer architectures, which are beset by quadratic computational complexity concerning input sequence length and substantial memory overhead due to the necessity of maintaining key-value caches. Although linear attention mechanisms have successfully reduced this burden in language models, our initial experiments reveal that they significantly degrade image generation quality because of their inability to capture critical long-range dependencies in visual data. We propose Linear Attention with Spatial-Aware Decay (LASAD), a novel attention mechanism that explicitly preserves genuine 2D spatial relationships within the flattened image sequences by computing position-dependent decay factors based on true 2D spatial location rather than 1D sequence positions. Based on this mechanism, we present LASADGen, an autoregressive image generator that enables selective attention to relevant spatial contexts with linear complexity. Experiments on ImageNet show LASADGen achieves state-of-the-art image generation performance and computational efficiency, bridging the gap between linear attention's efficiency and spatial understanding needed for high-quality generation.
On the Convergence of Gradient Descent on Learning Transformers with Residual Connections
Jun 05, 2025Abstract:Transformer models have emerged as fundamental tools across various scientific and engineering disciplines, owing to their outstanding performance in diverse applications. Despite this empirical success, the theoretical foundations of Transformers remain relatively underdeveloped, particularly in understanding their training dynamics. Existing research predominantly examines isolated components--such as self-attention mechanisms and feedforward networks--without thoroughly investigating the interdependencies between these components, especially when residual connections are present. In this paper, we aim to bridge this gap by analyzing the convergence behavior of a structurally complete yet single-layer Transformer, comprising self-attention, a feedforward network, and residual connections. We demonstrate that, under appropriate initialization, gradient descent exhibits a linear convergence rate, where the convergence speed is determined by the minimum and maximum singular values of the output matrix from the attention layer. Moreover, our analysis reveals that residual connections serve to ameliorate the ill-conditioning of this output matrix, an issue stemming from the low-rank structure imposed by the softmax operation, thereby promoting enhanced optimization stability. We also extend our theoretical findings to a multi-layer Transformer architecture, confirming the linear convergence rate of gradient descent under suitable initialization. Empirical results corroborate our theoretical insights, illustrating the beneficial role of residual connections in promoting convergence stability.
Hybrid Latent Reasoning via Reinforcement Learning
May 24, 2025Abstract:Recent advances in large language models (LLMs) have introduced latent reasoning as a promising alternative to autoregressive reasoning. By performing internal computation with hidden states from previous steps, latent reasoning benefit from more informative features rather than sampling a discrete chain-of-thought (CoT) path. Yet latent reasoning approaches are often incompatible with LLMs, as their continuous paradigm conflicts with the discrete nature of autoregressive generation. Moreover, these methods rely on CoT traces for training and thus fail to exploit the inherent reasoning patterns of LLMs. In this work, we explore latent reasoning by leveraging the intrinsic capabilities of LLMs via reinforcement learning (RL). To this end, we introduce hybrid reasoning policy optimization (HRPO), an RL-based hybrid latent reasoning approach that (1) integrates prior hidden states into sampled tokens with a learnable gating mechanism, and (2) initializes training with predominantly token embeddings while progressively incorporating more hidden features. This design maintains LLMs' generative capabilities and incentivizes hybrid reasoning using both discrete and continuous representations. In addition, the hybrid HRPO introduces stochasticity into latent reasoning via token sampling, thereby enabling RL-based optimization without requiring CoT trajectories. Extensive evaluations across diverse benchmarks show that HRPO outperforms prior methods in both knowledge- and reasoning-intensive tasks. Furthermore, HRPO-trained LLMs remain interpretable and exhibit intriguing behaviors like cross-lingual patterns and shorter completion lengths, highlighting the potential of our RL-based approach and offer insights for future work in latent reasoning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge