Liang Yan
LLM-based Multi-Agent Copilot for Quantum Sensor
Aug 07, 2025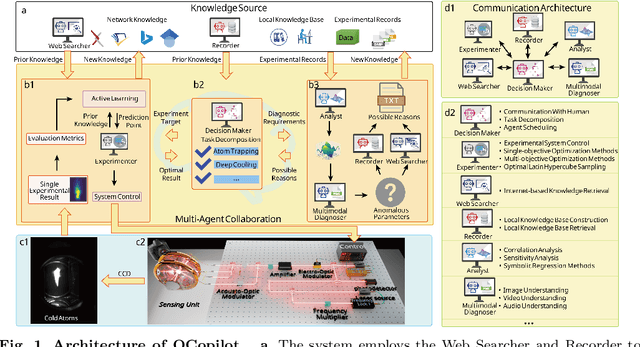
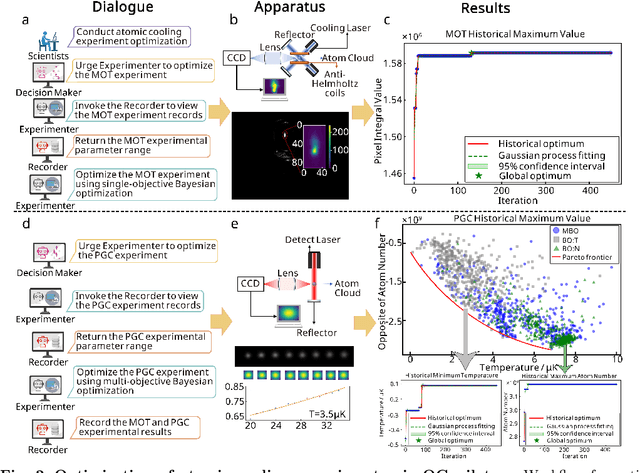
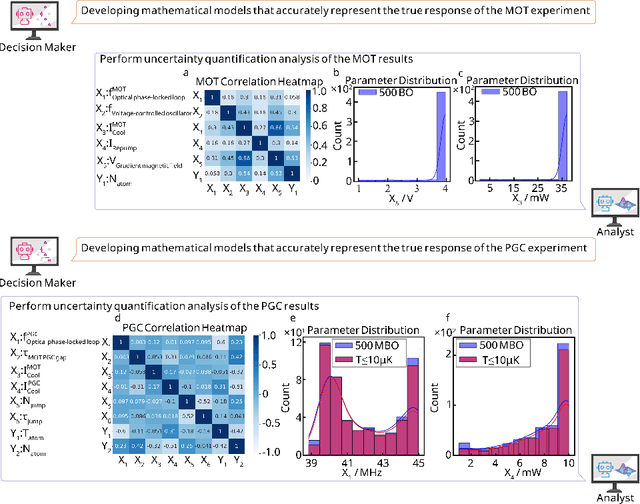
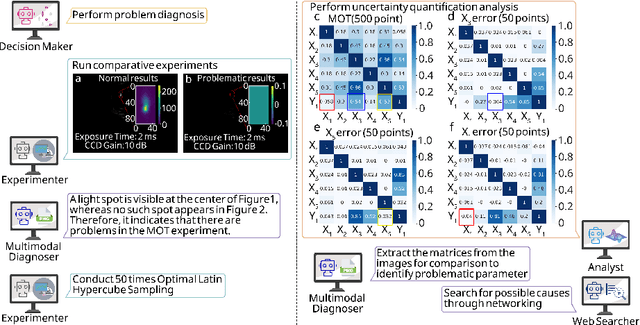
Abstract:Large language models (LLM) exhibit broad utility but face limitations in quantum sensor development, stemming from interdisciplinary knowledge barriers and involving complex optimization processes. Here we present QCopilot, an LLM-based multi-agent framework integrating external knowledge access, active learning, and uncertainty quantification for quantum sensor design and diagnosis. Comprising commercial LLMs with few-shot prompt engineering and vector knowledge base, QCopilot employs specialized agents to adaptively select optimization methods, automate modeling analysis, and independently perform problem diagnosis. Applying QCopilot to atom cooling experiments, we generated 10${}^{\rm{8}}$ sub-$\rm{\mu}$K atoms without any human intervention within a few hours, representing $\sim$100$\times$ speedup over manual experimentation. Notably, by continuously accumulating prior knowledge and enabling dynamic modeling, QCopilot can autonomously identify anomalous parameters in multi-parameter experimental settings. Our work reduces barriers to large-scale quantum sensor deployment and readily extends to other quantum information systems.
EVADE: Multimodal Benchmark for Evasive Content Detection in E-Commerce Applications
May 23, 2025Abstract:E-commerce platforms increasingly rely on Large Language Models (LLMs) and Vision-Language Models (VLMs) to detect illicit or misleading product content. However, these models remain vulnerable to evasive content: inputs (text or images) that superficially comply with platform policies while covertly conveying prohibited claims. Unlike traditional adversarial attacks that induce overt failures, evasive content exploits ambiguity and context, making it far harder to detect. Existing robustness benchmarks provide little guidance for this demanding, real-world challenge. We introduce EVADE, the first expert-curated, Chinese, multimodal benchmark specifically designed to evaluate foundation models on evasive content detection in e-commerce. The dataset contains 2,833 annotated text samples and 13,961 images spanning six demanding product categories, including body shaping, height growth, and health supplements. Two complementary tasks assess distinct capabilities: Single-Violation, which probes fine-grained reasoning under short prompts, and All-in-One, which tests long-context reasoning by merging overlapping policy rules into unified instructions. Notably, the All-in-One setting significantly narrows the performance gap between partial and full-match accuracy, suggesting that clearer rule definitions improve alignment between human and model judgment. We benchmark 26 mainstream LLMs and VLMs and observe substantial performance gaps: even state-of-the-art models frequently misclassify evasive samples. By releasing EVADE and strong baselines, we provide the first rigorous standard for evaluating evasive-content detection, expose fundamental limitations in current multimodal reasoning, and lay the groundwork for safer and more transparent content moderation systems in e-commerce. The dataset is publicly available at https://huggingface.co/datasets/koenshen/EVADE-Bench.
Deep decomposition method for the limited aperture inverse obstacle scattering problem
Mar 28, 2024Abstract:In this paper, we consider a deep learning approach to the limited aperture inverse obstacle scattering problem. It is well known that traditional deep learning relies solely on data, which may limit its performance for the inverse problem when only indirect observation data and a physical model are available. A fundamental question arises in light of these limitations: is it possible to enable deep learning to work on inverse problems without labeled data and to be aware of what it is learning? This work proposes a deep decomposition method (DDM) for such purposes, which does not require ground truth labels. It accomplishes this by providing physical operators associated with the scattering model to the neural network architecture. Additionally, a deep learning based data completion scheme is implemented in DDM to prevent distorting the solution of the inverse problem for limited aperture data. Furthermore, apart from addressing the ill-posedness imposed by the inverse problem itself, DDM is a physics-aware machine learning technique that can have interpretability property. The convergence result of DDM is theoretically proven. Numerical experiments are presented to demonstrate the validity of the proposed DDM even when the incident and observation apertures are extremely limited.
Adaptive operator learning for infinite-dimensional Bayesian inverse problems
Oct 27, 2023



Abstract:The fundamental computational issues in Bayesian inverse problems (BIPs) governed by partial differential equations (PDEs) stem from the requirement of repeated forward model evaluations. A popular strategy to reduce such cost is to replace expensive model simulations by computationally efficient approximations using operator learning, motivated by recent progresses in deep learning. However, using the approximated model directly may introduce a modeling error, exacerbating the already ill-posedness of inverse problems. Thus, balancing between accuracy and efficiency is essential for the effective implementation of such approaches. To this end, we develop an adaptive operator learning framework that can reduce modeling error gradually by forcing the surrogate to be accurate in local areas. This is accomplished by fine-tuning the pre-trained approximate model during the inversion process with adaptive points selected by a greedy algorithm, which requires only a few forward model evaluations. To validate our approach, we adopt DeepOnet to construct the surrogate and use unscented Kalman inversion (UKI) to approximate the solution of BIPs, respectively. Furthermore, we present rigorous convergence guarantee in the linear case using the framework of UKI. We test the approach on several benchmarks, including the Darcy flow, the heat source inversion problem, and the reaction diffusion problems. Numerical results demonstrate that our method can significantly reduce computational costs while maintaining inversion accuracy.
UNREAL:Unlabeled Nodes Retrieval and Labeling for Heavily-imbalanced Node Classification
Mar 18, 2023Abstract:Extremely skewed label distributions are common in real-world node classification tasks. If not dealt with appropriately, it significantly hurts the performance of GNNs in minority classes. Due to its practical importance, there have been a series of recent research devoted to this challenge. Existing over-sampling techniques smooth the label distribution by generating ``fake'' minority nodes and synthesizing their features and local topology, which largely ignore the rich information of unlabeled nodes on graphs. In this paper, we propose UNREAL, an iterative over-sampling method. The first key difference is that we only add unlabeled nodes instead of synthetic nodes, which eliminates the challenge of feature and neighborhood generation. To select which unlabeled nodes to add, we propose geometric ranking to rank unlabeled nodes. Geometric ranking exploits unsupervised learning in the node embedding space to effectively calibrates pseudo-label assignment. Finally, we identify the issue of geometric imbalance in the embedding space and provide a simple metric to filter out geometrically imbalanced nodes. Extensive experiments on real-world benchmark datasets are conducted, and the empirical results show that our method significantly outperforms current state-of-the-art methods consistent on different datasets with different imbalance ratios.
Failure-informed adaptive sampling for PINNs, Part II: combining with re-sampling and subset simulation
Feb 03, 2023



Abstract:This is the second part of our series works on failure-informed adaptive sampling for physic-informed neural networks (FI-PINNs). In our previous work \cite{gao2022failure}, we have presented an adaptive sampling framework by using the failure probability as the posterior error indicator, where the truncated Gaussian model has been adopted for estimating the indicator. In this work, we present two novel extensions to FI-PINNs. The first extension consist in combining with a re-sampling technique, so that the new algorithm can maintain a constant training size. This is achieved through a cosine-annealing, which gradually transforms the sampling of collocation points from uniform to adaptive via training progress. The second extension is to present the subset simulation algorithm as the posterior model (instead of the truncated Gaussian model) for estimating the error indicator, which can more effectively estimate the failure probability and generate new effective training points in the failure region. We investigate the performance of the new approach using several challenging problems, and numerical experiments demonstrate a significant improvement over the original algorithm.
Failure-informed adaptive sampling for PINNs
Oct 09, 2022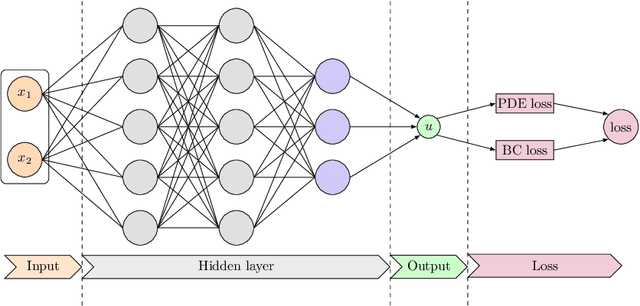
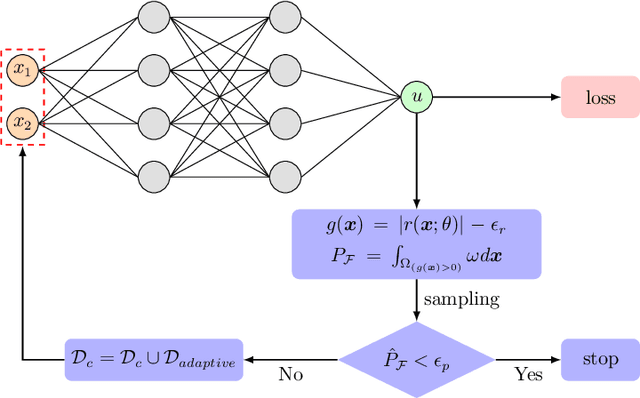
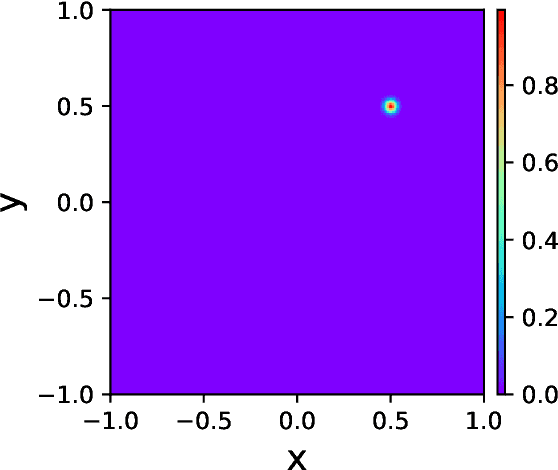

Abstract:Physics-informed neural networks (PINNs) have emerged as an effective technique for solving PDEs in a wide range of domains. It is noticed, however, the performance of PINNs can vary dramatically with different sampling procedures. For instance, a fixed set of (prior chosen) training points may fail to capture the effective solution region (especially for problems with singularities). To overcome this issue, we present in this work an adaptive strategy, termed the failure-informed PINNs (FI-PINNs), which is inspired by the viewpoint of reliability analysis. The key idea is to define an effective failure probability based on the residual, and then, with the aim of placing more samples in the failure region, the FI-PINNs employs a failure-informed enrichment technique to adaptively add new collocation points to the training set, such that the numerical accuracy is dramatically improved. In short, similar as adaptive finite element methods, the proposed FI-PINNs adopts the failure probability as the posterior error indicator to generate new training points. We prove rigorous error bounds of FI-PINNs and illustrate its performance through several problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge