Probabilistic Predictions of Process-Induced Deformation in Carbon/Epoxy Composites Using a Deep Operator Network

Fiber reinforcement and polymer matrix respond differently to manufacturing conditions due to mismatch in coefficient of thermal expansion and matrix shrinkage during curing of thermosets. These heterogeneities generate residual stresses over multiple length scales, whose partial release leads to process-induced deformation (PID), requiring accurate prediction and mitigation via optimized non-isothermal cure cycles. This study considers a unidirectional AS4 carbon fiber/amine bi-functional epoxy prepreg and models PID using a two-mechanism framework that accounts for thermal expansion/shrinkage and cure shrinkage. The model is validated against manufacturing trials to identify initial and boundary conditions, then used to generate PID responses for a diverse set of non-isothermal cure cycles (time-temperature profiles). Building on this physics-based foundation, we develop a data-driven surrogate based on Deep Operator Networks (DeepONets). A DeepONet is trained on a dataset combining high-fidelity simulations with targeted experimental measurements of PID. We extend this to a Feature-wise Linear Modulation (FiLM) DeepONet, where branch-network features are modulated by external parameters, including the initial degree of cure, enabling prediction of time histories of degree of cure, viscosity, and deformation. Because experimental data are available only at limited time instances (for example, final deformation), we use transfer learning: simulation-trained trunk and branch networks are fixed and only the final layer is updated using measured final deformation. Finally, we augment the framework with Ensemble Kalman Inversion (EKI) to quantify uncertainty under experimental conditions and to support optimization of cure schedules for reduced PID in composites.

Multi-Modal Robust Enhancement for Coastal Water Segmentation: A Systematic HSV-Guided Framework

Coastal water segmentation from satellite imagery presents unique challenges due to complex spectral characteristics and irregular boundary patterns. Traditional RGB-based approaches often suffer from training instability and poor generalization in diverse maritime environments. This paper introduces a systematic robust enhancement framework, referred to as Robust U-Net, that leverages HSV color space supervision and multi-modal constraints for improved coastal water segmentation. Our approach integrates five synergistic components: HSV-guided color supervision, gradient-based coastline optimization, morphological post-processing, sea area cleanup, and connectivity control. Through comprehensive ablation studies, we demonstrate that HSV supervision provides the highest impact (0.85 influence score), while the complete framework achieves superior training stability (84\% variance reduction) and enhanced segmentation quality. Our method shows consistent improvements across multiple evaluation metrics while maintaining computational efficiency. For reproducibility, our training configurations and code are available here: https://github.com/UofgCoastline/ICASSP-2026-Robust-Unet.

DeepSeek vs. ChatGPT: A Comparative Study for Scientific Computing and Scientific Machine Learning Tasks

Large Language Models (LLMs) have emerged as powerful tools for tackling a wide range of problems, including those in scientific computing, particularly in solving partial differential equations (PDEs). However, different models exhibit distinct strengths and preferences, resulting in varying levels of performance. In this paper, we compare the capabilities of the most advanced LLMs--ChatGPT and DeepSeek--along with their reasoning-optimized versions in addressing computational challenges. Specifically, we evaluate their proficiency in solving traditional numerical problems in scientific computing as well as leveraging scientific machine learning techniques for PDE-based problems. We designed all our experiments so that a non-trivial decision is required, e.g. defining the proper space of input functions for neural operator learning. Our findings reveal that the latest model, ChatGPT o3-mini-high, usually delivers the most accurate results while also responding significantly faster than its reasoning counterpart, DeepSeek R1. This enhanced speed and accuracy make ChatGPT o3-mini-high a more practical and efficient choice for diverse computational tasks at this juncture.

Scalable Bayesian Physics-Informed Kolmogorov-Arnold Networks

Uncertainty quantification (UQ) plays a pivotal role in scientific machine learning, especially when surrogate models are used to approximate complex systems. Although multilayer perceptions (MLPs) are commonly employed as surrogates, they often suffer from overfitting due to their large number of parameters. Kolmogorov-Arnold networks (KANs) offer an alternative solution with fewer parameters. However, gradient-based inference methods, such as Hamiltonian Monte Carlo (HMC), may result in computational inefficiency when applied to KANs, especially for large-scale datasets, due to the high cost of back-propagation.To address these challenges, we propose a novel approach, combining the dropout Tikhonov ensemble Kalman inversion (DTEKI) with Chebyshev KANs. This gradient-free method effectively mitigates overfitting and enhances numerical stability. Additionally, we incorporate the active subspace method to reduce the parameter-space dimensionality, allowing us to improve the accuracy of predictions and obtain more reliable uncertainty estimates.Extensive experiments demonstrate the efficacy of our approach in various test cases, including scenarios with large datasets and high noise levels. Our results show that the new method achieves comparable or better accuracy, much higher efficiency as well as stability compared to HMC, in addition to scalability. Moreover, by leveraging the low-dimensional parameter subspace, our method preserves prediction accuracy while substantially reducing further the computational cost.

Adaptive operator learning for infinite-dimensional Bayesian inverse problems

The fundamental computational issues in Bayesian inverse problems (BIPs) governed by partial differential equations (PDEs) stem from the requirement of repeated forward model evaluations. A popular strategy to reduce such cost is to replace expensive model simulations by computationally efficient approximations using operator learning, motivated by recent progresses in deep learning. However, using the approximated model directly may introduce a modeling error, exacerbating the already ill-posedness of inverse problems. Thus, balancing between accuracy and efficiency is essential for the effective implementation of such approaches. To this end, we develop an adaptive operator learning framework that can reduce modeling error gradually by forcing the surrogate to be accurate in local areas. This is accomplished by fine-tuning the pre-trained approximate model during the inversion process with adaptive points selected by a greedy algorithm, which requires only a few forward model evaluations. To validate our approach, we adopt DeepOnet to construct the surrogate and use unscented Kalman inversion (UKI) to approximate the solution of BIPs, respectively. Furthermore, we present rigorous convergence guarantee in the linear case using the framework of UKI. We test the approach on several benchmarks, including the Darcy flow, the heat source inversion problem, and the reaction diffusion problems. Numerical results demonstrate that our method can significantly reduce computational costs while maintaining inversion accuracy.

Failure-informed adaptive sampling for PINNs, Part II: combining with re-sampling and subset simulation

This is the second part of our series works on failure-informed adaptive sampling for physic-informed neural networks (FI-PINNs). In our previous work \cite{gao2022failure}, we have presented an adaptive sampling framework by using the failure probability as the posterior error indicator, where the truncated Gaussian model has been adopted for estimating the indicator. In this work, we present two novel extensions to FI-PINNs. The first extension consist in combining with a re-sampling technique, so that the new algorithm can maintain a constant training size. This is achieved through a cosine-annealing, which gradually transforms the sampling of collocation points from uniform to adaptive via training progress. The second extension is to present the subset simulation algorithm as the posterior model (instead of the truncated Gaussian model) for estimating the error indicator, which can more effectively estimate the failure probability and generate new effective training points in the failure region. We investigate the performance of the new approach using several challenging problems, and numerical experiments demonstrate a significant improvement over the original algorithm.

Failure-informed adaptive sampling for PINNs

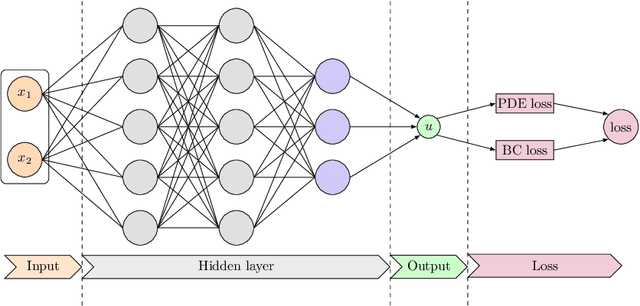
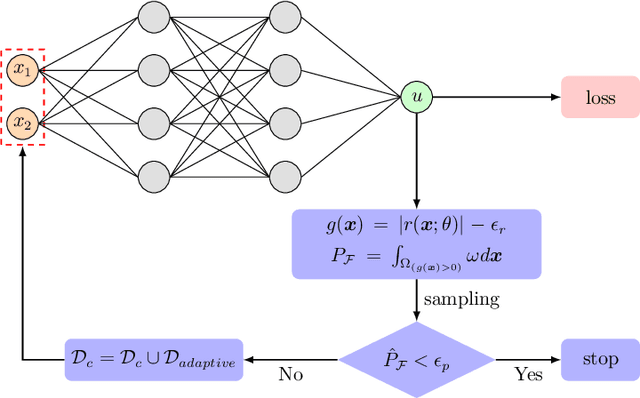
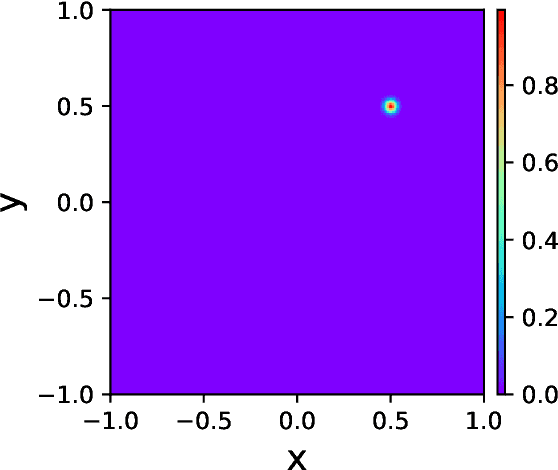
Physics-informed neural networks (PINNs) have emerged as an effective technique for solving PDEs in a wide range of domains. It is noticed, however, the performance of PINNs can vary dramatically with different sampling procedures. For instance, a fixed set of (prior chosen) training points may fail to capture the effective solution region (especially for problems with singularities). To overcome this issue, we present in this work an adaptive strategy, termed the failure-informed PINNs (FI-PINNs), which is inspired by the viewpoint of reliability analysis. The key idea is to define an effective failure probability based on the residual, and then, with the aim of placing more samples in the failure region, the FI-PINNs employs a failure-informed enrichment technique to adaptively add new collocation points to the training set, such that the numerical accuracy is dramatically improved. In short, similar as adaptive finite element methods, the proposed FI-PINNs adopts the failure probability as the posterior error indicator to generate new training points. We prove rigorous error bounds of FI-PINNs and illustrate its performance through several problems.

A Sufficient Condition for Convex Hull Property in General Convex Spatio-Temporal Corridors

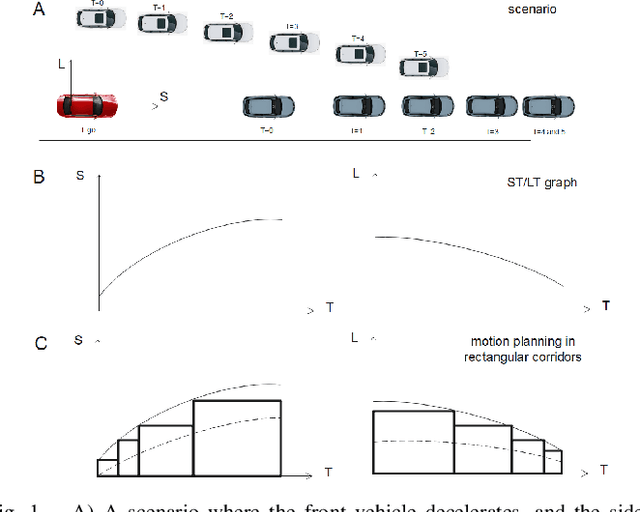
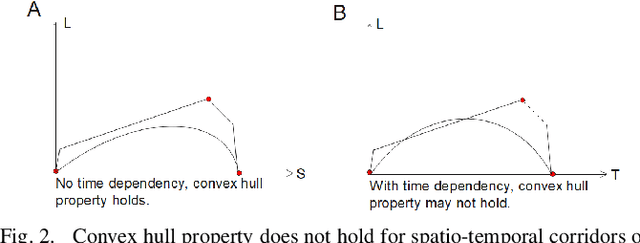
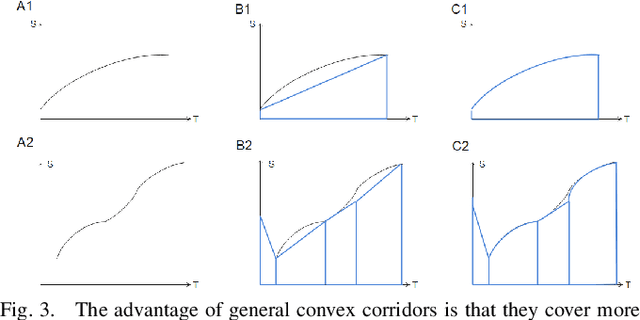
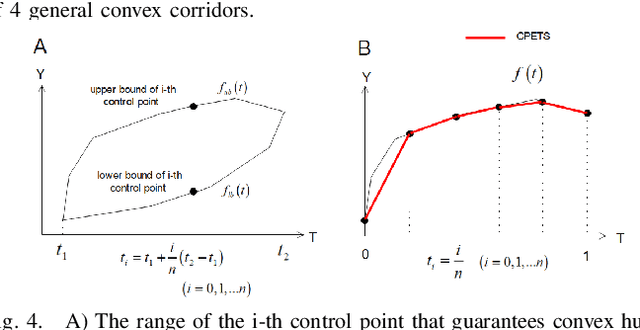
Motion planning is one of the key modules in autonomous driving systems to generate trajectories for self-driving vehicles to follow. A common motion planning approach is to generate trajectories within semantic safe corridors. The trajectories are generated by optimizing parametric curves (\textit{e.g.} Bezier curves) according to an objective function. To guarantee safety, the curves are required to satisfy the convex hull property, and be contained within the safety corridors. The convex hull property however does not necessary hold for time-dependent corridors, and depends on the shape of corridors. The existing approaches only support simple shape corridors, which is restrictive in real-world, complex scenarios. In this paper, we provide a sufficient condition for general convex, spatio-temporal corridors with theoretical proof of guaranteed convex hull property. The theorem allows for using more complicated shapes to generate spatio-temporal corridors and minimizing the uncovered search space to $O(\frac{1}{n^2})$ compared to $O(1)$ of trapezoidal corridors, which can improve the optimality of the solution. Simulation results show that using general convex corridors yields less harsh brakes, hence improving the overall smoothness of the resulting trajectories.