CAPS: Context-Aware Priority Sampling for Enhanced Imitation Learning in Autonomous Driving

In this paper, we introduce CAPS (Context-Aware Priority Sampling), a novel method designed to enhance data efficiency in learning-based autonomous driving systems. CAPS addresses the challenge of imbalanced training datasets in imitation learning by leveraging Vector Quantized Variational Autoencoders (VQ-VAEs). The use of VQ-VAE provides a structured and interpretable data representation, which helps reveal meaningful patterns in the data. These patterns are used to group the data into clusters, with each sample being assigned a cluster ID. The cluster IDs are then used to re-balance the dataset, ensuring that rare yet valuable samples receive higher priority during training. By ensuring a more diverse and informative training set, CAPS improves the generalization of the trained planner across a wide range of driving scenarios. We evaluate our method through closed-loop simulations in the CARLA environment. The results on Bench2Drive scenarios demonstrate that our framework outperforms state-of-the-art methods, leading to notable improvements in model performance.

Learning Soft Driving Constraints from Vectorized Scene Embeddings while Imitating Expert Trajectories

The primary goal of motion planning is to generate safe and efficient trajectories for vehicles. Traditionally, motion planning models are trained using imitation learning to mimic the behavior of human experts. However, these models often lack interpretability and fail to provide clear justifications for their decisions. We propose a method that integrates constraint learning into imitation learning by extracting driving constraints from expert trajectories. Our approach utilizes vectorized scene embeddings that capture critical spatial and temporal features, enabling the model to identify and generalize constraints across various driving scenarios. We formulate the constraint learning problem using a maximum entropy model, which scores the motion planner's trajectories based on their similarity to the expert trajectory. By separating the scoring process into distinct reward and constraint streams, we improve both the interpretability of the planner's behavior and its attention to relevant scene components. Unlike existing constraint learning methods that rely on simulators and are typically embedded in reinforcement learning (RL) or inverse reinforcement learning (IRL) frameworks, our method operates without simulators, making it applicable to a wider range of datasets and real-world scenarios. Experimental results on the InD and TrafficJams datasets demonstrate that incorporating driving constraints enhances model interpretability and improves closed-loop performance.

Learning from Mistakes: a Weakly-supervised Method for Mitigating the Distribution Shift in Autonomous Vehicle Planning

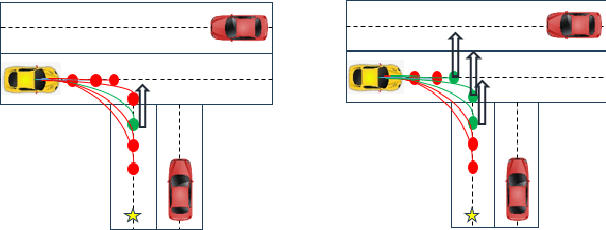
The planning problem constitutes a fundamental aspect of the autonomous driving framework. Recent strides in representation learning have empowered vehicles to comprehend their surrounding environments, thereby facilitating the integration of learning-based planning strategies. Among these approaches, Imitation Learning stands out due to its notable training efficiency. However, traditional Imitation Learning methodologies encounter challenges associated with the co-variate shift phenomenon. We propose Learn from Mistakes (LfM) as a remedy to address this issue. The essence of LfM lies in deploying a pre-trained planner across diverse scenarios. Instances where the planner deviates from its immediate objectives, such as maintaining a safe distance from obstacles or adhering to traffic rules, are flagged as mistakes. The environments corresponding to these mistakes are categorized as out-of-distribution states and compiled into a new dataset termed closed-loop mistakes dataset. Notably, the absence of expert annotations for the closed-loop data precludes the applicability of standard imitation learning approaches. To facilitate learning from the closed-loop mistakes, we introduce Validity Learning, a weakly supervised method, which aims to discern valid trajectories within the current environmental context. Experimental evaluations conducted on the InD and Nuplan datasets reveal substantial enhancements in closed-loop metrics such as Progress and Collision Rate, underscoring the effectiveness of the proposed methodology.

A Sufficient Condition for Convex Hull Property in General Convex Spatio-Temporal Corridors

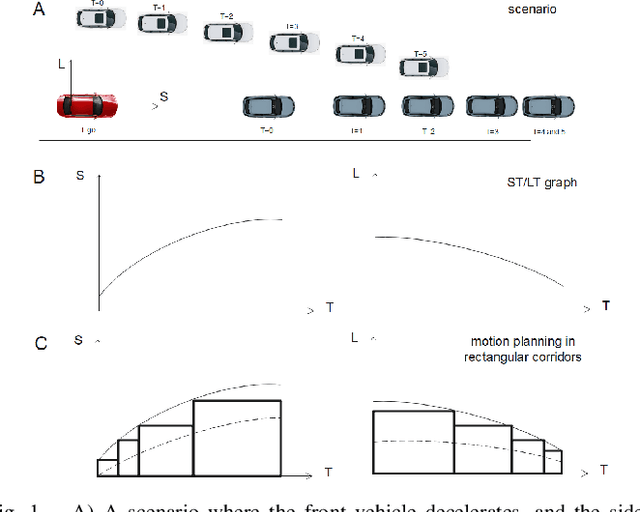
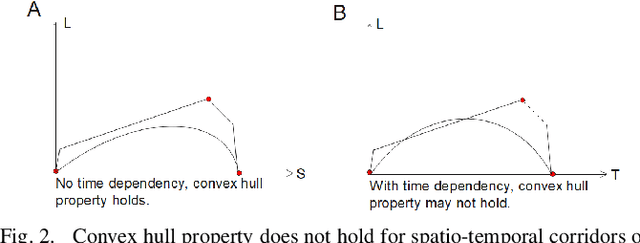
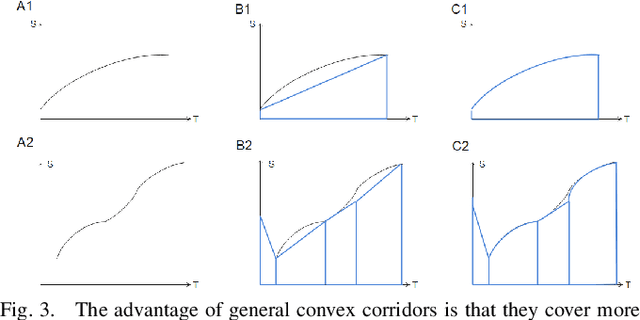
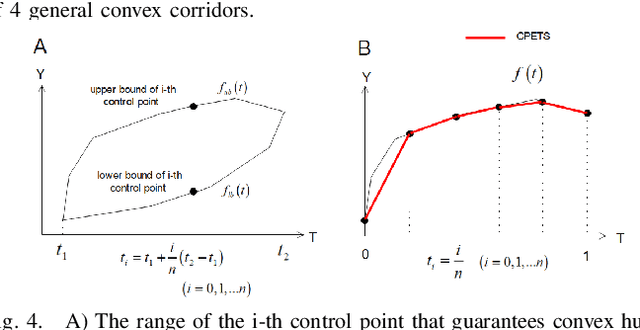
Motion planning is one of the key modules in autonomous driving systems to generate trajectories for self-driving vehicles to follow. A common motion planning approach is to generate trajectories within semantic safe corridors. The trajectories are generated by optimizing parametric curves (\textit{e.g.} Bezier curves) according to an objective function. To guarantee safety, the curves are required to satisfy the convex hull property, and be contained within the safety corridors. The convex hull property however does not necessary hold for time-dependent corridors, and depends on the shape of corridors. The existing approaches only support simple shape corridors, which is restrictive in real-world, complex scenarios. In this paper, we provide a sufficient condition for general convex, spatio-temporal corridors with theoretical proof of guaranteed convex hull property. The theorem allows for using more complicated shapes to generate spatio-temporal corridors and minimizing the uncovered search space to $O(\frac{1}{n^2})$ compared to $O(1)$ of trapezoidal corridors, which can improve the optimality of the solution. Simulation results show that using general convex corridors yields less harsh brakes, hence improving the overall smoothness of the resulting trajectories.