On Limitation of Transformer for Learning HMMs

Despite the remarkable success of Transformer-based architectures in various sequential modeling tasks, such as natural language processing, computer vision, and robotics, their ability to learn basic sequential models, like Hidden Markov Models (HMMs), is still unclear. This paper investigates the performance of Transformers in learning HMMs and their variants through extensive experimentation and compares them to Recurrent Neural Networks (RNNs). We show that Transformers consistently underperform RNNs in both training speed and testing accuracy across all tested HMM models. There are even challenging HMM instances where Transformers struggle to learn, while RNNs can successfully do so. Our experiments further reveal the relation between the depth of Transformers and the longest sequence length it can effectively learn, based on the types and the complexity of HMMs. To address the limitation of transformers in modeling HMMs, we demonstrate that a variant of the Chain-of-Thought (CoT), called $\textit{block CoT}$ in the training phase, can help transformers to reduce the evaluation error and to learn longer sequences at a cost of increasing the training time. Finally, we complement our empirical findings by theoretical results proving the expressiveness of transformers in approximating HMMs with logarithmic depth.

ZeroSwap: Data-driven Optimal Market Making in DeFi

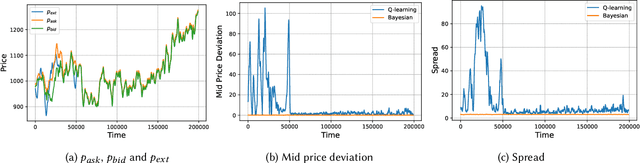
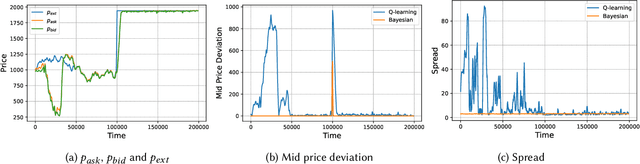
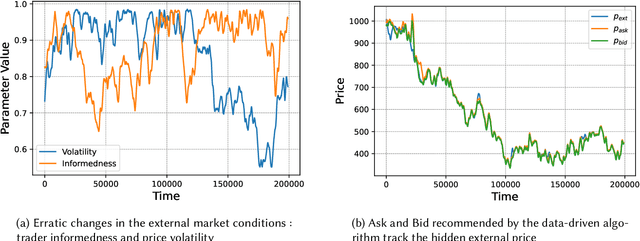
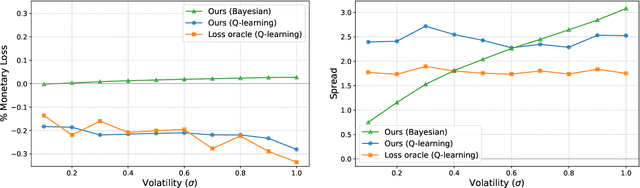
Automated Market Makers (AMMs) are major centers of matching liquidity supply and demand in Decentralized Finance. Their functioning relies primarily on the presence of liquidity providers (LPs) incentivized to invest their assets into a liquidity pool. However, the prices at which a pooled asset is traded is often more stale than the prices on centralized and more liquid exchanges. This leads to the LPs suffering losses to arbitrage. This problem is addressed by adapting market prices to trader behavior, captured via the classical market microstructure model of Glosten and Milgrom. In this paper, we propose the first optimal Bayesian and the first model-free data-driven algorithm to optimally track the external price of the asset. The notion of optimality that we use enforces a zero-profit condition on the prices of the market maker, hence the name ZeroSwap. This ensures that the market maker balances losses to informed traders with profits from noise traders. The key property of our approach is the ability to estimate the external market price without the need for price oracles or loss oracles. Our theoretical guarantees on the performance of both these algorithms, ensuring the stability and convergence of their price recommendations, are of independent interest in the theory of reinforcement learning. We empirically demonstrate the robustness of our algorithms to changing market conditions.

Provably Efficient Exploration in Quantum Reinforcement Learning with Logarithmic Worst-Case Regret

While quantum reinforcement learning (RL) has attracted a surge of attention recently, its theoretical understanding is limited. In particular, it remains elusive how to design provably efficient quantum RL algorithms that can address the exploration-exploitation trade-off. To this end, we propose a novel UCRL-style algorithm that takes advantage of quantum computing for tabular Markov decision processes (MDPs) with $S$ states, $A$ actions, and horizon $H$, and establish an $\mathcal{O}(\mathrm{poly}(S, A, H, \log T))$ worst-case regret for it, where $T$ is the number of episodes. Furthermore, we extend our results to quantum RL with linear function approximation, which is capable of handling problems with large state spaces. Specifically, we develop a quantum algorithm based on value target regression (VTR) for linear mixture MDPs with $d$-dimensional linear representation and prove that it enjoys $\mathcal{O}(\mathrm{poly}(d, H, \log T))$ regret. Our algorithms are variants of UCRL/UCRL-VTR algorithms in classical RL, which also leverage a novel combination of lazy updating mechanisms and quantum estimation subroutines. This is the key to breaking the $\Omega(\sqrt{T})$-regret barrier in classical RL. To the best of our knowledge, this is the first work studying the online exploration in quantum RL with provable logarithmic worst-case regret.

Provable Sim-to-real Transfer in Continuous Domain with Partial Observations

Sim-to-real transfer trains RL agents in the simulated environments and then deploys them in the real world. Sim-to-real transfer has been widely used in practice because it is often cheaper, safer and much faster to collect samples in simulation than in the real world. Despite the empirical success of the sim-to-real transfer, its theoretical foundation is much less understood. In this paper, we study the sim-to-real transfer in continuous domain with partial observations, where the simulated environments and real-world environments are modeled by linear quadratic Gaussian (LQG) systems. We show that a popular robust adversarial training algorithm is capable of learning a policy from the simulated environment that is competitive to the optimal policy in the real-world environment. To achieve our results, we design a new algorithm for infinite-horizon average-cost LQGs and establish a regret bound that depends on the intrinsic complexity of the model class. Our algorithm crucially relies on a novel history clipping scheme, which might be of independent interest.

Near-Optimal Reward-Free Exploration for Linear Mixture MDPs with Plug-in Solver

Although model-based reinforcement learning (RL) approaches are considered more sample efficient, existing algorithms are usually relying on sophisticated planning algorithm to couple tightly with the model-learning procedure. Hence the learned models may lack the ability of being re-used with more specialized planners. In this paper we address this issue and provide approaches to learn an RL model efficiently without the guidance of a reward signal. In particular, we take a plug-in solver approach, where we focus on learning a model in the exploration phase and demand that \emph{any planning algorithm} on the learned model can give a near-optimal policy. Specicially, we focus on the linear mixture MDP setting, where the probability transition matrix is a (unknown) convex combination of a set of existing models. We show that, by establishing a novel exploration algorithm, the plug-in approach learns a model by taking $\tilde{O}(d^2H^3/\epsilon^2)$ interactions with the environment and \emph{any} $\epsilon$-optimal planner on the model gives an $O(\epsilon)$-optimal policy on the original model. This sample complexity matches lower bounds for non-plug-in approaches and is \emph{statistically optimal}. We achieve this result by leveraging a careful maximum total-variance bound using Bernstein inequality and properties specified to linear mixture MDP.

Understanding Domain Randomization for Sim-to-real Transfer

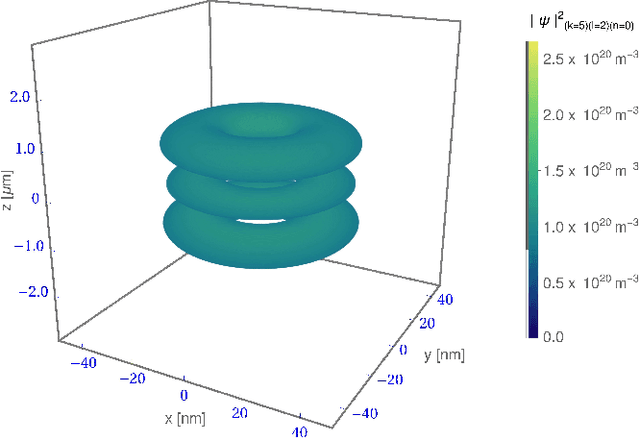
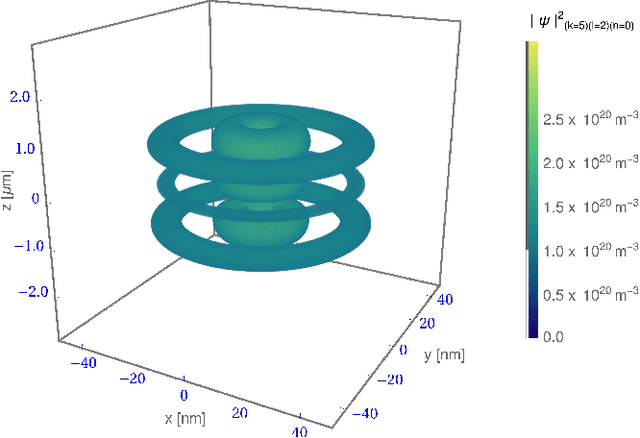
Reinforcement learning encounters many challenges when applied directly in the real world. Sim-to-real transfer is widely used to transfer the knowledge learned from simulation to the real world. Domain randomization -- one of the most popular algorithms for sim-to-real transfer -- has been demonstrated to be effective in various tasks in robotics and autonomous driving. Despite its empirical successes, theoretical understanding on why this simple algorithm works is limited. In this paper, we propose a theoretical framework for sim-to-real transfers, in which the simulator is modeled as a set of MDPs with tunable parameters (corresponding to unknown physical parameters such as friction). We provide sharp bounds on the sim-to-real gap -- the difference between the value of policy returned by domain randomization and the value of an optimal policy for the real world. We prove that sim-to-real transfer can succeed under mild conditions without any real-world training samples. Our theory also highlights the importance of using memory (i.e., history-dependent policies) in domain randomization. Our proof is based on novel techniques that reduce the problem of bounding the sim-to-real gap to the problem of designing efficient learning algorithms for infinite-horizon MDPs, which we believe are of independent interest.

Near-optimal Representation Learning for Linear Bandits and Linear RL

This paper studies representation learning for multi-task linear bandits and multi-task episodic RL with linear value function approximation. We first consider the setting where we play $M$ linear bandits with dimension $d$ concurrently, and these bandits share a common $k$-dimensional linear representation so that $k\ll d$ and $k \ll M$. We propose a sample-efficient algorithm, MTLR-OFUL, which leverages the shared representation to achieve $\tilde{O}(M\sqrt{dkT} + d\sqrt{kMT} )$ regret, with $T$ being the number of total steps. Our regret significantly improves upon the baseline $\tilde{O}(Md\sqrt{T})$ achieved by solving each task independently. We further develop a lower bound that shows our regret is near-optimal when $d > M$. Furthermore, we extend the algorithm and analysis to multi-task episodic RL with linear value function approximation under low inherent Bellman error \citep{zanette2020learning}. To the best of our knowledge, this is the first theoretical result that characterizes the benefits of multi-task representation learning for exploration in RL with function approximation.

Efficient Reinforcement Learning in Factored MDPs with Application to Constrained RL

Reinforcement learning (RL) in episodic, factored Markov decision processes (FMDPs) is studied. We propose an algorithm called FMDP-BF, which leverages the factorization structure of FMDP. The regret of FMDP-BF is shown to be exponentially smaller than that of optimal algorithms designed for non-factored MDPs, and improves on the best previous result for FMDPs~\citep{osband2014near} by a factored of $\sqrt{H|\mathcal{S}_i|}$, where $|\mathcal{S}_i|$ is the cardinality of the factored state subspace and $H$ is the planning horizon. To show the optimality of our bounds, we also provide a lower bound for FMDP, which indicates that our algorithm is near-optimal w.r.t. timestep $T$, horizon $H$ and factored state-action subspace cardinality. Finally, as an application, we study a new formulation of constrained RL, known as RL with knapsack constraints (RLwK), and provides the first sample-efficient algorithm based on FMDP-BF.

Distributed Bandit Learning: Near-Optimal Regret with Efficient Communication

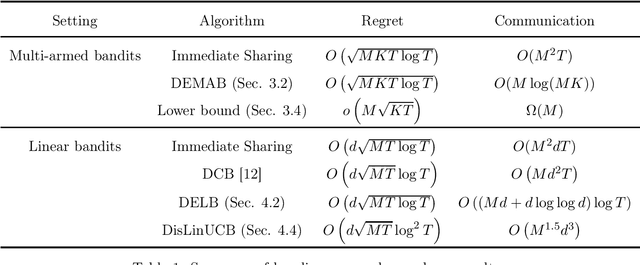
We study the problem of regret minimization for distributed bandits learning, in which $M$ agents work collaboratively to minimize their total regret under the coordination of a central server. Our goal is to design communication protocols with near-optimal regret and little communication cost, which is measured by the total amount of transmitted data. For distributed multi-armed bandits, we propose a protocol with near-optimal regret and only $O(M\log(MK))$ communication cost, where $K$ is the number of arms. The communication cost is independent of the time horizon $T$, has only logarithmic dependence on the number of arms, and matches the lower bound except for a logarithmic factor. For distributed $d$-dimensional linear bandits, we propose a protocol that achieves near-optimal regret and has communication cost of order $\tilde{O}(Md)$, which has only logarithmic dependence on $T$.