ZeroSwap: Data-driven Optimal Market Making in DeFi

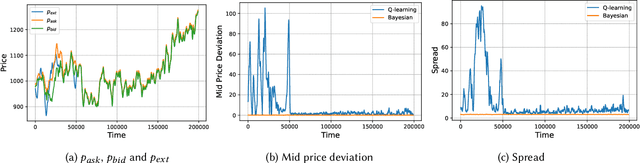
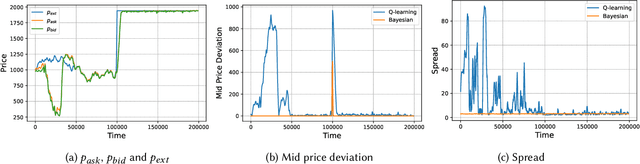
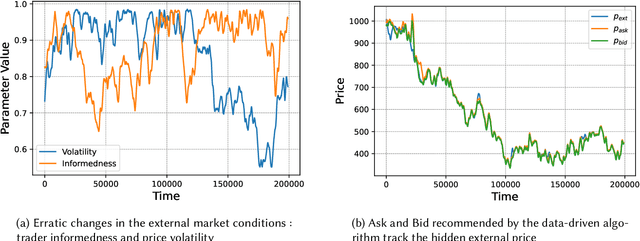
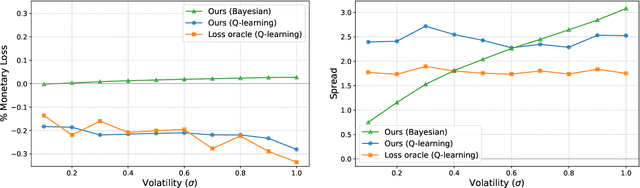
Automated Market Makers (AMMs) are major centers of matching liquidity supply and demand in Decentralized Finance. Their functioning relies primarily on the presence of liquidity providers (LPs) incentivized to invest their assets into a liquidity pool. However, the prices at which a pooled asset is traded is often more stale than the prices on centralized and more liquid exchanges. This leads to the LPs suffering losses to arbitrage. This problem is addressed by adapting market prices to trader behavior, captured via the classical market microstructure model of Glosten and Milgrom. In this paper, we propose the first optimal Bayesian and the first model-free data-driven algorithm to optimally track the external price of the asset. The notion of optimality that we use enforces a zero-profit condition on the prices of the market maker, hence the name ZeroSwap. This ensures that the market maker balances losses to informed traders with profits from noise traders. The key property of our approach is the ability to estimate the external market price without the need for price oracles or loss oracles. Our theoretical guarantees on the performance of both these algorithms, ensuring the stability and convergence of their price recommendations, are of independent interest in the theory of reinforcement learning. We empirically demonstrate the robustness of our algorithms to changing market conditions.

Communication Algorithms via Deep Learning

Coding theory is a central discipline underpinning wireline and wireless modems that are the workhorses of the information age. Progress in coding theory is largely driven by individual human ingenuity with sporadic breakthroughs over the past century. In this paper we study whether it is possible to automate the discovery of decoding algorithms via deep learning. We study a family of sequential codes parameterized by recurrent neural network (RNN) architectures. We show that creatively designed and trained RNN architectures can decode well known sequential codes such as the convolutional and turbo codes with close to optimal performance on the additive white Gaussian noise (AWGN) channel, which itself is achieved by breakthrough algorithms of our times (Viterbi and BCJR decoders, representing dynamic programing and forward-backward algorithms). We show strong generalizations, i.e., we train at a specific signal to noise ratio and block length but test at a wide range of these quantities, as well as robustness and adaptivity to deviations from the AWGN setting.