MINDGAMES: A Live Arena for Evaluating Social and Strategic Reasoning in Multi-Agent LLMs

Large language models (LLMs) are increasingly deployed as interactive agents, yet their capacity for social and strategic reasoning over extended interaction remains poorly understood. Existing evaluations rely on static vignettes or single-game benchmarks that cannot capture the sustained, multi-faceted reasoning that real-world multi-agent settings demand. We introduce Mindgames, a multi-game arena and evaluation platform for LLM agents that operationalizes complementary reasoning demands relevant to ``theory of mind'': belief attribution under hidden information, opponent modeling through repeated strategic interaction, cooperative inference under knowledge asymmetries, and sustained deception in social deduction. Built on TextArena, Mindgames provides a unified interaction interface, TrueSkill-based rating, and full trajectory logging across four game environments. We instantiate Mindgames through a 2025 competition cycle hosted at a major AI conference, which assessed 944 submitted agents from 76 teams across four games: Colonel Blotto, Iterated Prisoner's Dilemma, Codenames, and Secret Mafia. Our analysis surfaces both agent-level and evaluation-level limitations: brittle rule adherence remains a major bottleneck, top-performing systems repeatedly rely on explicit structural scaffolding, and leaderboard validity differs sharply across environments. In particular, failure-heavy environments can reward robustness to opponent errors as much as strategic ability, with Secret Mafia exhibiting a pronounced error-survival confound in this cycle. We release a dataset of 29,571 multi-agent games with turn-level observations, actions, and rewards, together with MG-Ref, a deterministic offline tournament protocol that scores new agents against a frozen reference pool of top-ranked, low-error Stage~II submissions under the same error-attribution lens used in this analysis.

Influencing Bandits: Arm Selection for Preference Shaping

We consider a non stationary multi-armed bandit in which the population preferences are positively and negatively reinforced by the observed rewards. The objective of the algorithm is to shape the population preferences to maximize the fraction of the population favouring a predetermined arm. For the case of binary opinions, two types of opinion dynamics are considered -- decreasing elasticity (modeled as a Polya urn with increasing number of balls) and constant elasticity (using the voter model). For the first case, we describe an Explore-then-commit policy and a Thompson sampling policy and analyse the regret for each of these policies. We then show that these algorithms and their analyses carry over to the constant elasticity case. We also describe a Thompson sampling based algorithm for the case when more than two types of opinions are present. Finally, we discuss the case where presence of multiple recommendation systems gives rise to a trade-off between their popularity and opinion shaping objectives.

ZeroSwap: Data-driven Optimal Market Making in DeFi

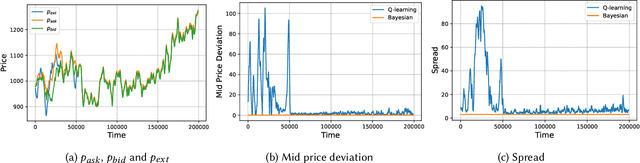
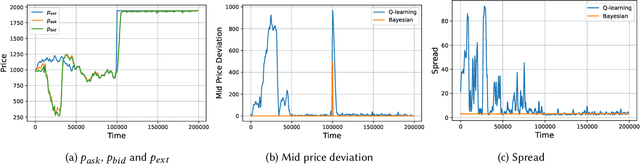
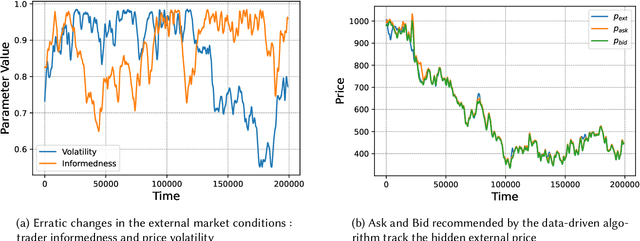
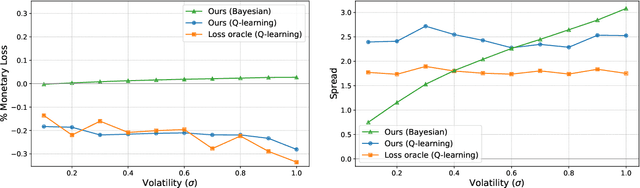
Automated Market Makers (AMMs) are major centers of matching liquidity supply and demand in Decentralized Finance. Their functioning relies primarily on the presence of liquidity providers (LPs) incentivized to invest their assets into a liquidity pool. However, the prices at which a pooled asset is traded is often more stale than the prices on centralized and more liquid exchanges. This leads to the LPs suffering losses to arbitrage. This problem is addressed by adapting market prices to trader behavior, captured via the classical market microstructure model of Glosten and Milgrom. In this paper, we propose the first optimal Bayesian and the first model-free data-driven algorithm to optimally track the external price of the asset. The notion of optimality that we use enforces a zero-profit condition on the prices of the market maker, hence the name ZeroSwap. This ensures that the market maker balances losses to informed traders with profits from noise traders. The key property of our approach is the ability to estimate the external market price without the need for price oracles or loss oracles. Our theoretical guarantees on the performance of both these algorithms, ensuring the stability and convergence of their price recommendations, are of independent interest in the theory of reinforcement learning. We empirically demonstrate the robustness of our algorithms to changing market conditions.

CRISP: Curriculum based Sequential Neural Decoders for Polar Code Family

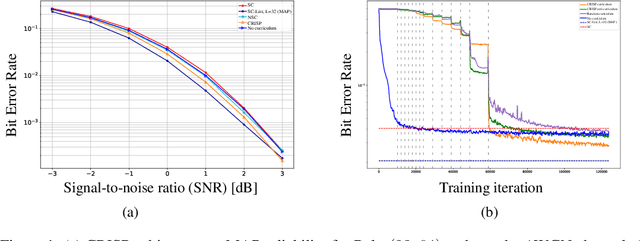
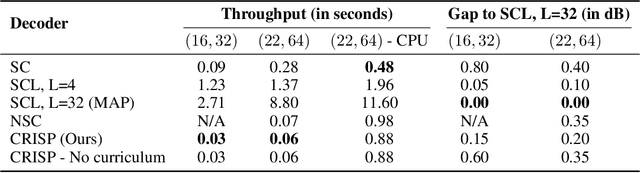
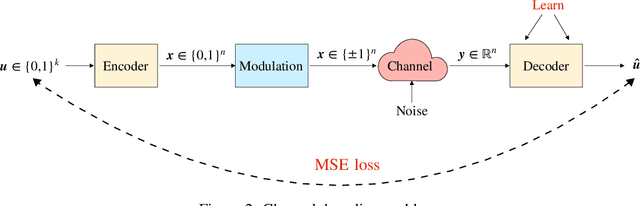
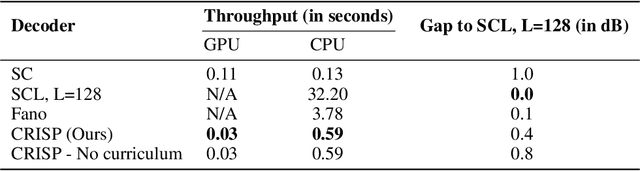
Polar codes are widely used state-of-the-art codes for reliable communication that have recently been included in the 5th generation wireless standards (5G). However, there remains room for the design of polar decoders that are both efficient and reliable in the short blocklength regime. Motivated by recent successes of data-driven channel decoders, we introduce a novel $\textbf{C}$ur$\textbf{RI}$culum based $\textbf{S}$equential neural decoder for $\textbf{P}$olar codes (CRISP). We design a principled curriculum, guided by information-theoretic insights, to train CRISP and show that it outperforms the successive-cancellation (SC) decoder and attains near-optimal reliability performance on the Polar(16,32) and Polar(22, 64) codes. The choice of the proposed curriculum is critical in achieving the accuracy gains of CRISP, as we show by comparing against other curricula. More notably, CRISP can be readily extended to Polarization-Adjusted-Convolutional (PAC) codes, where existing SC decoders are significantly less reliable. To the best of our knowledge, CRISP constructs the first data-driven decoder for PAC codes and attains near-optimal performance on the PAC(16, 32) code.