ZeroSwap: Data-driven Optimal Market Making in DeFi
Paper and Code
Oct 13, 2023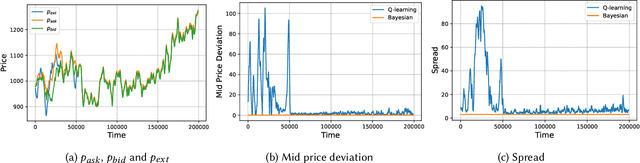
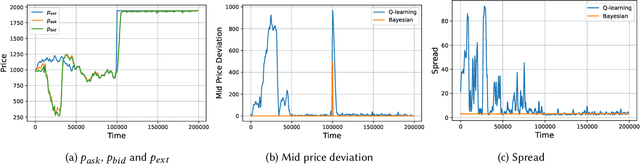
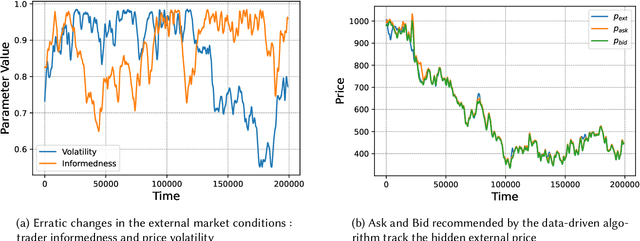
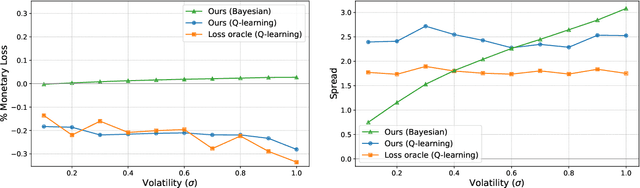
Automated Market Makers (AMMs) are major centers of matching liquidity supply and demand in Decentralized Finance. Their functioning relies primarily on the presence of liquidity providers (LPs) incentivized to invest their assets into a liquidity pool. However, the prices at which a pooled asset is traded is often more stale than the prices on centralized and more liquid exchanges. This leads to the LPs suffering losses to arbitrage. This problem is addressed by adapting market prices to trader behavior, captured via the classical market microstructure model of Glosten and Milgrom. In this paper, we propose the first optimal Bayesian and the first model-free data-driven algorithm to optimally track the external price of the asset. The notion of optimality that we use enforces a zero-profit condition on the prices of the market maker, hence the name ZeroSwap. This ensures that the market maker balances losses to informed traders with profits from noise traders. The key property of our approach is the ability to estimate the external market price without the need for price oracles or loss oracles. Our theoretical guarantees on the performance of both these algorithms, ensuring the stability and convergence of their price recommendations, are of independent interest in the theory of reinforcement learning. We empirically demonstrate the robustness of our algorithms to changing market conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge