Task Arithmetic Through The Lens Of One-Shot Federated Learning

Task Arithmetic is a model merging technique that enables the combination of multiple models' capabilities into a single model through simple arithmetic in the weight space, without the need for additional fine-tuning or access to the original training data. However, the factors that determine the success of Task Arithmetic remain unclear. In this paper, we examine Task Arithmetic for multi-task learning by framing it as a one-shot Federated Learning problem. We demonstrate that Task Arithmetic is mathematically equivalent to the commonly used algorithm in Federated Learning, called Federated Averaging (FedAvg). By leveraging well-established theoretical results from FedAvg, we identify two key factors that impact the performance of Task Arithmetic: data heterogeneity and training heterogeneity. To mitigate these challenges, we adapt several algorithms from Federated Learning to improve the effectiveness of Task Arithmetic. Our experiments demonstrate that applying these algorithms can often significantly boost performance of the merged model compared to the original Task Arithmetic approach. This work bridges Task Arithmetic and Federated Learning, offering new theoretical perspectives on Task Arithmetic and improved practical methodologies for model merging.

Asymptotically Optimal Change Detection for Unnormalized Pre- and Post-Change Distributions

This paper addresses the problem of detecting changes when only unnormalized pre- and post-change distributions are accessible. This situation happens in many scenarios in physics such as in ferromagnetism, crystallography, magneto-hydrodynamics, and thermodynamics, where the energy models are difficult to normalize. Our approach is based on the estimation of the Cumulative Sum (CUSUM) statistics, which is known to produce optimal performance. We first present an intuitively appealing approximation method. Unfortunately, this produces a biased estimator of the CUSUM statistics and may cause performance degradation. We then propose the Log-Partition Approximation Cumulative Sum (LPA-CUSUM) algorithm based on thermodynamic integration (TI) in order to estimate the log-ratio of normalizing constants of pre- and post-change distributions. It is proved that this approach gives an unbiased estimate of the log-partition function and the CUSUM statistics, and leads to an asymptotically optimal performance. Moreover, we derive a relationship between the required sample size for thermodynamic integration and the desired detection delay performance, offering guidelines for practical parameter selection. Numerical studies are provided demonstrating the efficacy of our approach.

On the Convergence of a Federated Expectation-Maximization Algorithm

Data heterogeneity has been a long-standing bottleneck in studying the convergence rates of Federated Learning algorithms. In order to better understand the issue of data heterogeneity, we study the convergence rate of the Expectation-Maximization (EM) algorithm for the Federated Mixture of $K$ Linear Regressions model. We fully characterize the convergence rate of the EM algorithm under all regimes of $m/n$ where $m$ is the number of clients and $n$ is the number of data points per client. We show that with a signal-to-noise-ratio (SNR) of order $\Omega(\sqrt{K})$, the well-initialized EM algorithm converges within the minimax distance of the ground truth under each of the regimes. Interestingly, we identify that when $m$ grows exponentially in $n$, the EM algorithm only requires a constant number of iterations to converge. We perform experiments on synthetic datasets to illustrate our results. Surprisingly, the results show that rather than being a bottleneck, data heterogeneity can accelerate the convergence of federated learning algorithms.

Self-Play with Adversarial Critic: Provable and Scalable Offline Alignment for Language Models

This work studies the challenge of aligning large language models (LLMs) with offline preference data. We focus on alignment by Reinforcement Learning from Human Feedback (RLHF) in particular. While popular preference optimization methods exhibit good empirical performance in practice, they are not theoretically guaranteed to converge to the optimal policy and can provably fail when the data coverage is sparse by classical offline reinforcement learning (RL) results. On the other hand, a recent line of work has focused on theoretically motivated preference optimization methods with provable guarantees, but these are not computationally efficient for large-scale applications like LLM alignment. To bridge this gap, we propose SPAC, a new offline preference optimization method with self-play, inspired by the on-average pessimism technique from the offline RL literature, to be the first provable and scalable approach to LLM alignment. We both provide theoretical analysis for its convergence under single-policy concentrability for the general function approximation setting and demonstrate its competitive empirical performance for LLM alignment on a 7B Mistral model with Open LLM Leaderboard evaluations.

Reinforcement Learning Paycheck Optimization for Multivariate Financial Goals

We study paycheck optimization, which examines how to allocate income in order to achieve several competing financial goals. For paycheck optimization, a quantitative methodology is missing, due to a lack of a suitable problem formulation. To deal with this issue, we formulate the problem as a utility maximization problem. The proposed formulation is able to (i) unify different financial goals; (ii) incorporate user preferences regarding the goals; (iii) handle stochastic interest rates. The proposed formulation also facilitates an end-to-end reinforcement learning solution, which is implemented on a variety of problem settings.

Stochastic Approximation with Delayed Updates: Finite-Time Rates under Markovian Sampling

Motivated by applications in large-scale and multi-agent reinforcement learning, we study the non-asymptotic performance of stochastic approximation (SA) schemes with delayed updates under Markovian sampling. While the effect of delays has been extensively studied for optimization, the manner in which they interact with the underlying Markov process to shape the finite-time performance of SA remains poorly understood. In this context, our first main contribution is to show that under time-varying bounded delays, the delayed SA update rule guarantees exponentially fast convergence of the \emph{last iterate} to a ball around the SA operator's fixed point. Notably, our bound is \emph{tight} in its dependence on both the maximum delay $\tau_{max}$, and the mixing time $\tau_{mix}$. To achieve this tight bound, we develop a novel inductive proof technique that, unlike various existing delayed-optimization analyses, relies on establishing uniform boundedness of the iterates. As such, our proof may be of independent interest. Next, to mitigate the impact of the maximum delay on the convergence rate, we provide the first finite-time analysis of a delay-adaptive SA scheme under Markovian sampling. In particular, we show that the exponent of convergence of this scheme gets scaled down by $\tau_{avg}$, as opposed to $\tau_{max}$ for the vanilla delayed SA rule; here, $\tau_{avg}$ denotes the average delay across all iterations. Moreover, the adaptive scheme requires no prior knowledge of the delay sequence for step-size tuning. Our theoretical findings shed light on the finite-time effects of delays for a broad class of algorithms, including TD learning, Q-learning, and stochastic gradient descent under Markovian sampling.

A general theory for robust clustering via trimmed mean

Clustering is a fundamental tool in statistical machine learning in the presence of heterogeneous data. Many recent results focus primarily on optimal mislabeling guarantees, when data are distributed around centroids with sub-Gaussian errors. Yet, the restrictive sub-Gaussian model is often invalid in practice, since various real-world applications exhibit heavy tail distributions around the centroids or suffer from possible adversarial attacks that call for robust clustering with a robust data-driven initialization. In this paper, we introduce a hybrid clustering technique with a novel multivariate trimmed mean type centroid estimate to produce mislabeling guarantees under a weak initialization condition for general error distributions around the centroids. A matching lower bound is derived, up to factors depending on the number of clusters. In addition, our approach also produces the optimal mislabeling even in the presence of adversarial outliers. Our results reduce to the sub-Gaussian case when errors follow sub-Gaussian distributions. To solve the problem thoroughly, we also present novel data-driven robust initialization techniques and show that, with probabilities approaching one, these initial centroid estimates are sufficiently good for the subsequent clustering algorithm to achieve the optimal mislabeling rates. Furthermore, we demonstrate that the Lloyd algorithm is suboptimal for more than two clusters even when errors are Gaussian, and for two clusters when errors distributions have heavy tails. Both simulated data and real data examples lend further support to both of our robust initialization procedure and clustering algorithm.

ZeroSwap: Data-driven Optimal Market Making in DeFi

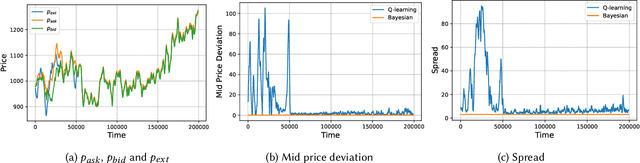
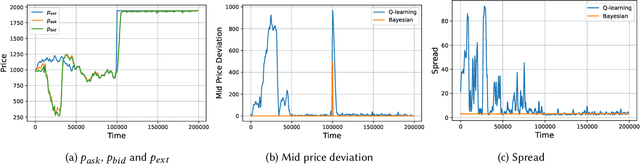
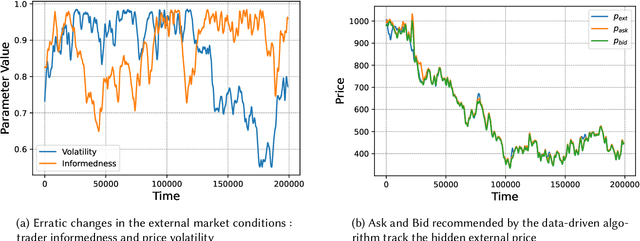
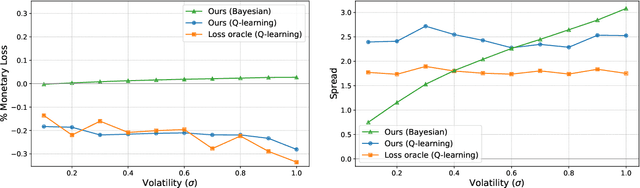
Automated Market Makers (AMMs) are major centers of matching liquidity supply and demand in Decentralized Finance. Their functioning relies primarily on the presence of liquidity providers (LPs) incentivized to invest their assets into a liquidity pool. However, the prices at which a pooled asset is traded is often more stale than the prices on centralized and more liquid exchanges. This leads to the LPs suffering losses to arbitrage. This problem is addressed by adapting market prices to trader behavior, captured via the classical market microstructure model of Glosten and Milgrom. In this paper, we propose the first optimal Bayesian and the first model-free data-driven algorithm to optimally track the external price of the asset. The notion of optimality that we use enforces a zero-profit condition on the prices of the market maker, hence the name ZeroSwap. This ensures that the market maker balances losses to informed traders with profits from noise traders. The key property of our approach is the ability to estimate the external market price without the need for price oracles or loss oracles. Our theoretical guarantees on the performance of both these algorithms, ensuring the stability and convergence of their price recommendations, are of independent interest in the theory of reinforcement learning. We empirically demonstrate the robustness of our algorithms to changing market conditions.

Adversarially robust clustering with optimality guarantees

We consider the problem of clustering data points coming from sub-Gaussian mixtures. Existing methods that provably achieve the optimal mislabeling error, such as the Lloyd algorithm, are usually vulnerable to outliers. In contrast, clustering methods seemingly robust to adversarial perturbations are not known to satisfy the optimal statistical guarantees. We propose a simple algorithm that obtains the optimal mislabeling rate even when we allow adversarial outliers to be present. Our algorithm achieves the optimal error rate in constant iterations when a weak initialization condition is satisfied. In the absence of outliers, in fixed dimensions, our theoretical guarantees are similar to that of the Lloyd algorithm. Extensive experiments on various simulated data sets are conducted to support the theoretical guarantees of our method.

Real Time Analytics: Algorithms and Systems

Velocity is one of the 4 Vs commonly used to characterize Big Data. In this regard, Forrester remarked the following in Q3 2014: "The high velocity, white-water flow of data from innumerable real-time data sources such as market data, Internet of Things, mobile, sensors, click-stream, and even transactions remain largely unnavigated by most firms. The opportunity to leverage streaming analytics has never been greater." Example use cases of streaming analytics include, but not limited to: (a) visualization of business metrics in real-time (b) facilitating highly personalized experiences (c) expediting response during emergencies. Streaming analytics is extensively used in a wide variety of domains such as healthcare, e-commerce, financial services, telecommunications, energy and utilities, manufacturing, government and transportation. In this tutorial, we shall present an in-depth overview of streaming analytics - applications, algorithms and platforms - landscape. We shall walk through how the field has evolved over the last decade and then discuss the current challenges - the impact of the other three Vs, viz., Volume, Variety and Veracity, on Big Data streaming analytics. The tutorial is intended for both researchers and practitioners in the industry. We shall also present state-of-the-affairs of streaming analytics at Twitter.