Asymptotically Optimal Change Detection for Unnormalized Pre- and Post-Change Distributions

This paper addresses the problem of detecting changes when only unnormalized pre- and post-change distributions are accessible. This situation happens in many scenarios in physics such as in ferromagnetism, crystallography, magneto-hydrodynamics, and thermodynamics, where the energy models are difficult to normalize. Our approach is based on the estimation of the Cumulative Sum (CUSUM) statistics, which is known to produce optimal performance. We first present an intuitively appealing approximation method. Unfortunately, this produces a biased estimator of the CUSUM statistics and may cause performance degradation. We then propose the Log-Partition Approximation Cumulative Sum (LPA-CUSUM) algorithm based on thermodynamic integration (TI) in order to estimate the log-ratio of normalizing constants of pre- and post-change distributions. It is proved that this approach gives an unbiased estimate of the log-partition function and the CUSUM statistics, and leads to an asymptotically optimal performance. Moreover, we derive a relationship between the required sample size for thermodynamic integration and the desired detection delay performance, offering guidelines for practical parameter selection. Numerical studies are provided demonstrating the efficacy of our approach.

DASA: Delay-Adaptive Multi-Agent Stochastic Approximation

We consider a setting in which $N$ agents aim to speedup a common Stochastic Approximation (SA) problem by acting in parallel and communicating with a central server. We assume that the up-link transmissions to the server are subject to asynchronous and potentially unbounded time-varying delays. To mitigate the effect of delays and stragglers while reaping the benefits of distributed computation, we propose \texttt{DASA}, a Delay-Adaptive algorithm for multi-agent Stochastic Approximation. We provide a finite-time analysis of \texttt{DASA} assuming that the agents' stochastic observation processes are independent Markov chains. Significantly advancing existing results, \texttt{DASA} is the first algorithm whose convergence rate depends only on the mixing time $\tau_{mix}$ and on the average delay $\tau_{avg}$ while jointly achieving an $N$-fold convergence speedup under Markovian sampling. Our work is relevant for various SA applications, including multi-agent and distributed temporal difference (TD) learning, Q-learning and stochastic optimization with correlated data.

Stochastic Approximation with Delayed Updates: Finite-Time Rates under Markovian Sampling

Motivated by applications in large-scale and multi-agent reinforcement learning, we study the non-asymptotic performance of stochastic approximation (SA) schemes with delayed updates under Markovian sampling. While the effect of delays has been extensively studied for optimization, the manner in which they interact with the underlying Markov process to shape the finite-time performance of SA remains poorly understood. In this context, our first main contribution is to show that under time-varying bounded delays, the delayed SA update rule guarantees exponentially fast convergence of the \emph{last iterate} to a ball around the SA operator's fixed point. Notably, our bound is \emph{tight} in its dependence on both the maximum delay $\tau_{max}$, and the mixing time $\tau_{mix}$. To achieve this tight bound, we develop a novel inductive proof technique that, unlike various existing delayed-optimization analyses, relies on establishing uniform boundedness of the iterates. As such, our proof may be of independent interest. Next, to mitigate the impact of the maximum delay on the convergence rate, we provide the first finite-time analysis of a delay-adaptive SA scheme under Markovian sampling. In particular, we show that the exponent of convergence of this scheme gets scaled down by $\tau_{avg}$, as opposed to $\tau_{max}$ for the vanilla delayed SA rule; here, $\tau_{avg}$ denotes the average delay across all iterations. Moreover, the adaptive scheme requires no prior knowledge of the delay sequence for step-size tuning. Our theoretical findings shed light on the finite-time effects of delays for a broad class of algorithms, including TD learning, Q-learning, and stochastic gradient descent under Markovian sampling.

Score-Based Methods for Discrete Optimization in Deep Learning

Discrete optimization problems often arise in deep learning tasks, despite the fact that neural networks typically operate on continuous data. One class of these problems involve objective functions which depend on neural networks, but optimization variables which are discrete. Although the discrete optimization literature provides efficient algorithms, they are still impractical in these settings due to the high cost of an objective function evaluation, which involves a neural network forward-pass. In particular, they require $O(n)$ complexity per iteration, but real data such as point clouds have values of $n$ in thousands or more. In this paper, we investigate a score-based approximation framework to solve such problems. This framework uses a score function as a proxy for the marginal gain of the objective, leveraging embeddings of the discrete variables and speed of auto-differentiation frameworks to compute backward-passes in parallel. We experimentally demonstrate, in adversarial set classification tasks, that our method achieves a superior trade-off in terms of speed and solution quality compared to heuristic methods.

Min-Max Optimization under Delays

Delays and asynchrony are inevitable in large-scale machine-learning problems where communication plays a key role. As such, several works have extensively analyzed stochastic optimization with delayed gradients. However, as far as we are aware, no analogous theory is available for min-max optimization, a topic that has gained recent popularity due to applications in adversarial robustness, game theory, and reinforcement learning. Motivated by this gap, we examine the performance of standard min-max optimization algorithms with delayed gradient updates. First, we show (empirically) that even small delays can cause prominent algorithms like Extra-gradient (\texttt{EG}) to diverge on simple instances for which \texttt{EG} guarantees convergence in the absence of delays. Our empirical study thus suggests the need for a careful analysis of delayed versions of min-max optimization algorithms. Accordingly, under suitable technical assumptions, we prove that Gradient Descent-Ascent (\texttt{GDA}) and \texttt{EG} with delayed updates continue to guarantee convergence to saddle points for convex-concave and strongly convex-strongly concave settings. Our complexity bounds reveal, in a transparent manner, the slow-down in convergence caused by delays.

Collaborative Linear Bandits with Adversarial Agents: Near-Optimal Regret Bounds

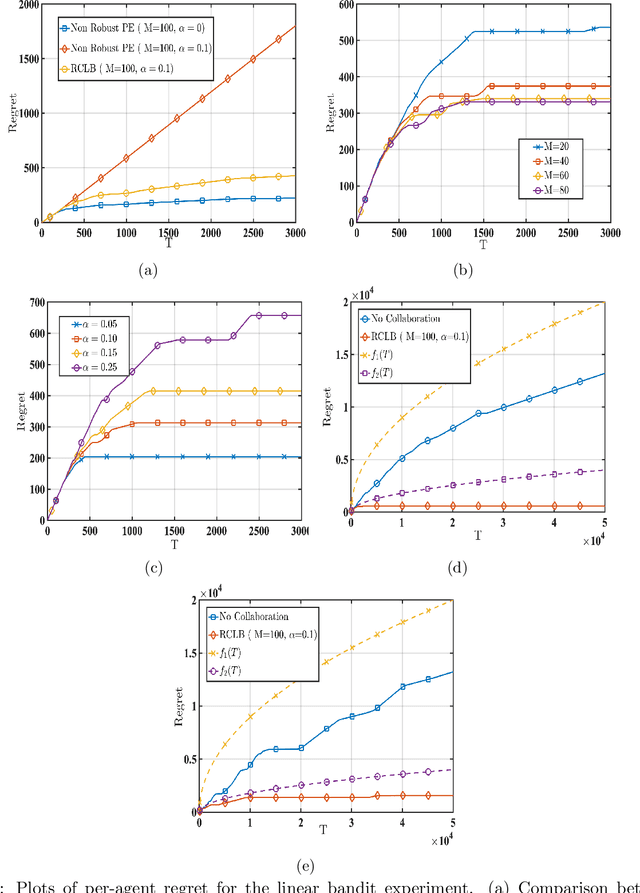
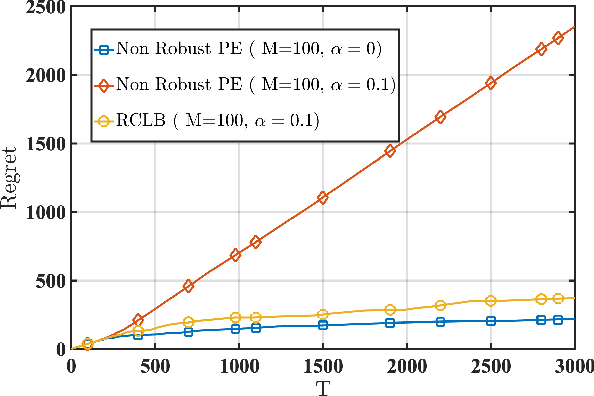
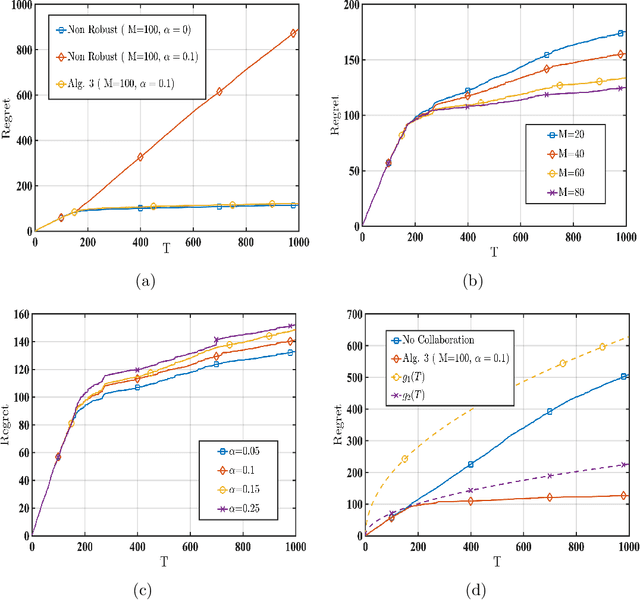
We consider a linear stochastic bandit problem involving $M$ agents that can collaborate via a central server to minimize regret. A fraction $\alpha$ of these agents are adversarial and can act arbitrarily, leading to the following tension: while collaboration can potentially reduce regret, it can also disrupt the process of learning due to adversaries. In this work, we provide a fundamental understanding of this tension by designing new algorithms that balance the exploration-exploitation trade-off via carefully constructed robust confidence intervals. We also complement our algorithms with tight analyses. First, we develop a robust collaborative phased elimination algorithm that achieves $\tilde{O}\left(\alpha+ 1/\sqrt{M}\right) \sqrt{dT}$ regret for each good agent; here, $d$ is the model-dimension and $T$ is the horizon. For small $\alpha$, our result thus reveals a clear benefit of collaboration despite adversaries. Using an information-theoretic argument, we then prove a matching lower bound, thereby providing the first set of tight, near-optimal regret bounds for collaborative linear bandits with adversaries. Furthermore, by leveraging recent advances in high-dimensional robust statistics, we significantly extend our algorithmic ideas and results to (i) the generalized linear bandit model that allows for non-linear observation maps; and (ii) the contextual bandit setting that allows for time-varying feature vectors.

Distributed Statistical Min-Max Learning in the Presence of Byzantine Agents

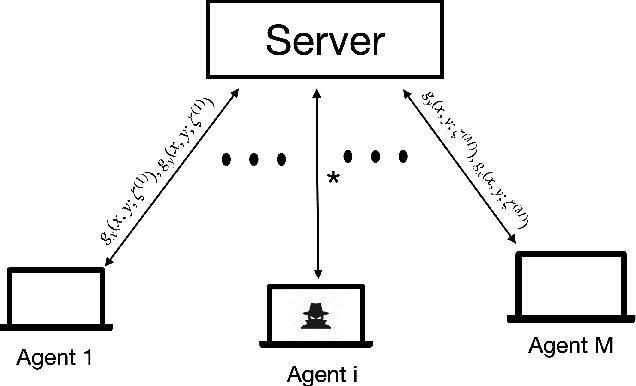
Recent years have witnessed a growing interest in the topic of min-max optimization, owing to its relevance in the context of generative adversarial networks (GANs), robust control and optimization, and reinforcement learning. Motivated by this line of work, we consider a multi-agent min-max learning problem, and focus on the emerging challenge of contending with worst-case Byzantine adversarial agents in such a setup. By drawing on recent results from robust statistics, we design a robust distributed variant of the extra-gradient algorithm - a popular algorithmic approach for min-max optimization. Our main contribution is to provide a crisp analysis of the proposed robust extra-gradient algorithm for smooth convex-concave and smooth strongly convex-strongly concave functions. Specifically, we establish statistical rates of convergence to approximate saddle points. Our rates are near-optimal, and reveal both the effect of adversarial corruption and the benefit of collaboration among the non-faulty agents. Notably, this is the first paper to provide formal theoretical guarantees for large-scale distributed min-max learning in the presence of adversarial agents.

Minimax Optimization: The Case of Convex-Submodular

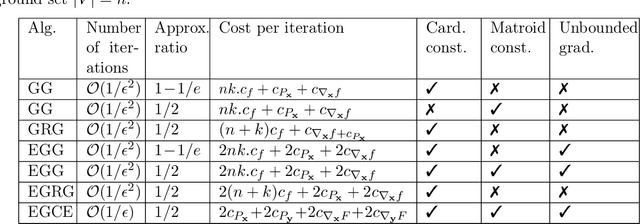
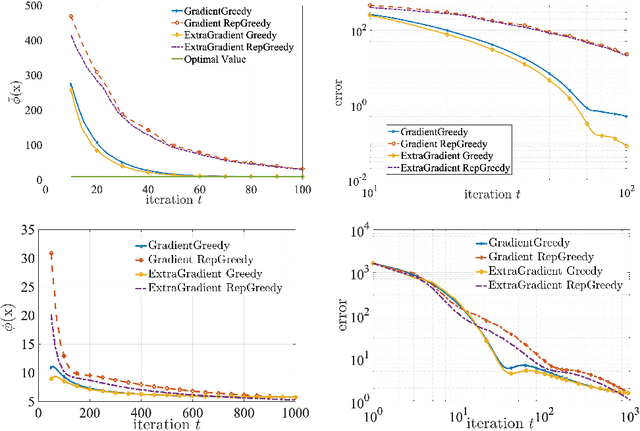
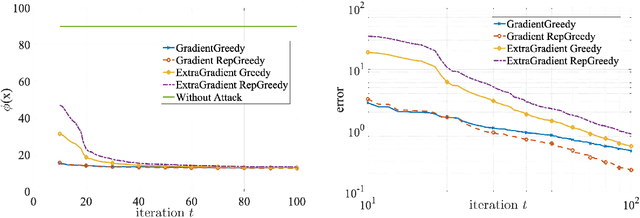
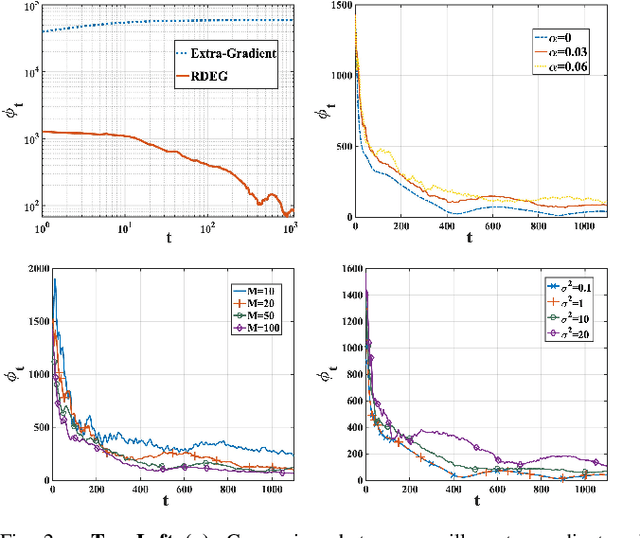
Minimax optimization has been central in addressing various applications in machine learning, game theory, and control theory. Prior literature has thus far mainly focused on studying such problems in the continuous domain, e.g., convex-concave minimax optimization is now understood to a significant extent. Nevertheless, minimax problems extend far beyond the continuous domain to mixed continuous-discrete domains or even fully discrete domains. In this paper, we study mixed continuous-discrete minimax problems where the minimization is over a continuous variable belonging to Euclidean space and the maximization is over subsets of a given ground set. We introduce the class of convex-submodular minimax problems, where the objective is convex with respect to the continuous variable and submodular with respect to the discrete variable. Even though such problems appear frequently in machine learning applications, little is known about how to address them from algorithmic and theoretical perspectives. For such problems, we first show that obtaining saddle points are hard up to any approximation, and thus introduce new notions of (near-) optimality. We then provide several algorithmic procedures for solving convex and monotone-submodular minimax problems and characterize their convergence rates, computational complexity, and quality of the final solution according to our notions of optimally. Our proposed algorithms are iterative and combine tools from both discrete and continuous optimization. Finally, we provide numerical experiments to showcase the effectiveness of our purposed methods.

Submodular Meta-Learning

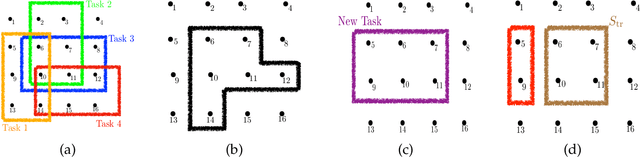
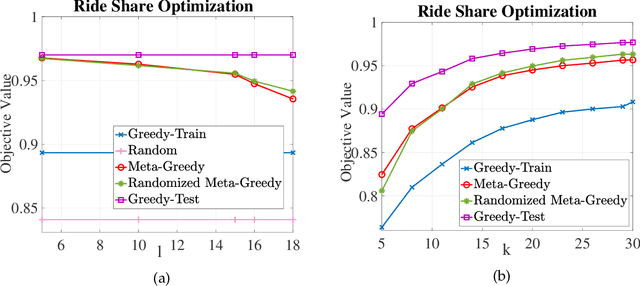
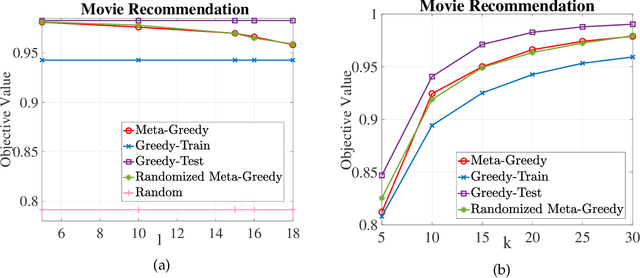
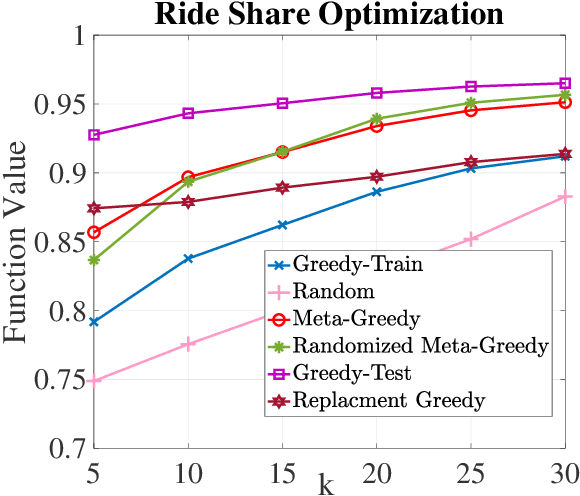
In this paper, we introduce a discrete variant of the meta-learning framework. Meta-learning aims at exploiting prior experience and data to improve performance on future tasks. By now, there exist numerous formulations for meta-learning in the continuous domain. Notably, the Model-Agnostic Meta-Learning (MAML) formulation views each task as a continuous optimization problem and based on prior data learns a suitable initialization that can be adapted to new, unseen tasks after a few simple gradient updates. Motivated by this terminology, we propose a novel meta-learning framework in the discrete domain where each task is equivalent to maximizing a set function under a cardinality constraint. Our approach aims at using prior data, i.e., previously visited tasks, to train a proper initial solution set that can be quickly adapted to a new task at a relatively low computational cost. This approach leads to (i) a personalized solution for each individual task, and (ii) significantly reduced computational cost at test time compared to the case where the solution is fully optimized once the new task is revealed. The training procedure is performed by solving a challenging discrete optimization problem for which we present deterministic and randomized algorithms. In the case where the tasks are monotone and submodular, we show strong theoretical guarantees for our proposed methods even though the training objective may not be submodular. We also demonstrate the effectiveness of our framework on two real-world problem instances where we observe that our methods lead to a significant reduction in computational complexity in solving the new tasks while incurring a small performance loss compared to when the tasks are fully optimized.

Optimal Algorithms for Submodular Maximization with Distributed Constraints

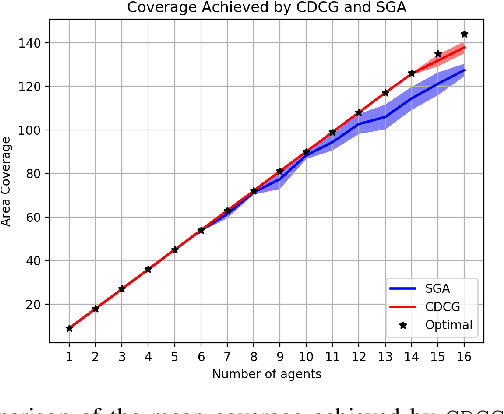
We consider a class of discrete optimization problems that aim to maximize a submodular objective function subject to a distributed partition matroid constraint. More precisely, we consider a networked scenario in which multiple agents choose actions from local strategy sets with the goal of maximizing a submodular objective function defined over the set of all possible actions. Given this distributed setting, we develop Constraint-Distributed Continuous Greedy (CDCG), a message passing algorithm that converges to the tight $(1-1/e)$ approximation factor of the optimum global solution using only local computation and communication. It is known that a sequential greedy algorithm can only achieve a $1/2$ multiplicative approximation of the optimal solution for this class of problems in the distributed setting. Our framework relies on lifting the discrete problem to a continuous domain and developing a consensus algorithm that achieves the tight $(1-1/e)$ approximation guarantee of the global discrete solution once a proper rounding scheme is applied. We also offer empirical results from a multi-agent area coverage problem to show that the proposed method significantly outperforms the state-of-the-art sequential greedy method.