Distributed Statistical Min-Max Learning in the Presence of Byzantine Agents
Paper and Code
Apr 07, 2022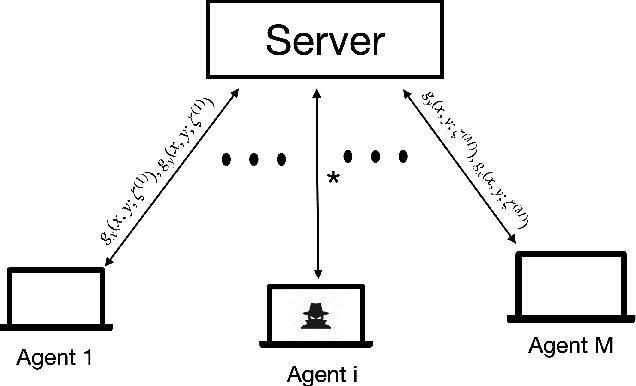
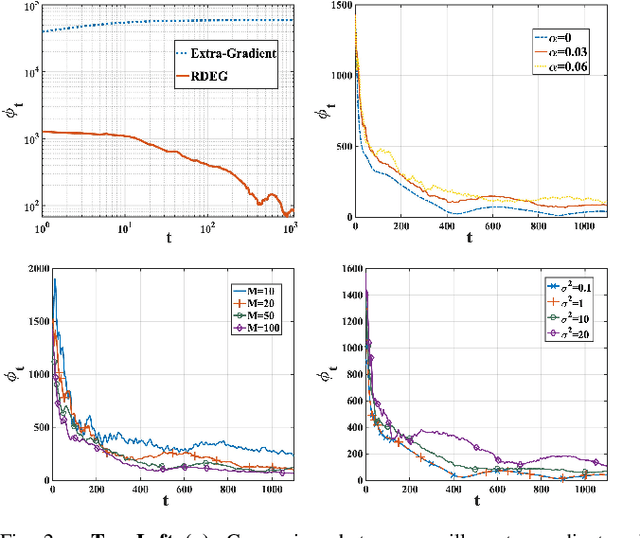
Recent years have witnessed a growing interest in the topic of min-max optimization, owing to its relevance in the context of generative adversarial networks (GANs), robust control and optimization, and reinforcement learning. Motivated by this line of work, we consider a multi-agent min-max learning problem, and focus on the emerging challenge of contending with worst-case Byzantine adversarial agents in such a setup. By drawing on recent results from robust statistics, we design a robust distributed variant of the extra-gradient algorithm - a popular algorithmic approach for min-max optimization. Our main contribution is to provide a crisp analysis of the proposed robust extra-gradient algorithm for smooth convex-concave and smooth strongly convex-strongly concave functions. Specifically, we establish statistical rates of convergence to approximate saddle points. Our rates are near-optimal, and reveal both the effect of adversarial corruption and the benefit of collaboration among the non-faulty agents. Notably, this is the first paper to provide formal theoretical guarantees for large-scale distributed min-max learning in the presence of adversarial agents.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge