Optimal Algorithms for Submodular Maximization with Distributed Constraints
Paper and Code
Sep 30, 2019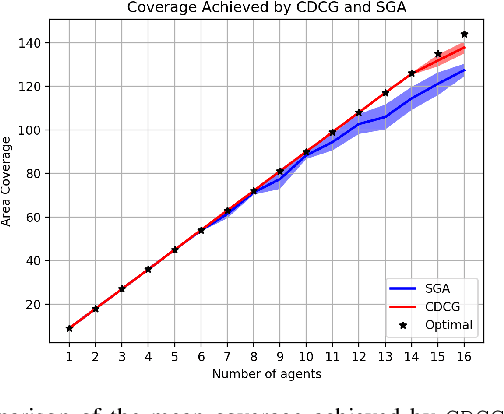
We consider a class of discrete optimization problems that aim to maximize a submodular objective function subject to a distributed partition matroid constraint. More precisely, we consider a networked scenario in which multiple agents choose actions from local strategy sets with the goal of maximizing a submodular objective function defined over the set of all possible actions. Given this distributed setting, we develop Constraint-Distributed Continuous Greedy (CDCG), a message passing algorithm that converges to the tight $(1-1/e)$ approximation factor of the optimum global solution using only local computation and communication. It is known that a sequential greedy algorithm can only achieve a $1/2$ multiplicative approximation of the optimal solution for this class of problems in the distributed setting. Our framework relies on lifting the discrete problem to a continuous domain and developing a consensus algorithm that achieves the tight $(1-1/e)$ approximation guarantee of the global discrete solution once a proper rounding scheme is applied. We also offer empirical results from a multi-agent area coverage problem to show that the proposed method significantly outperforms the state-of-the-art sequential greedy method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge