Conformal Risk Minimization with Variance Reduction

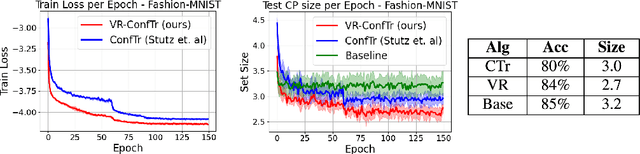
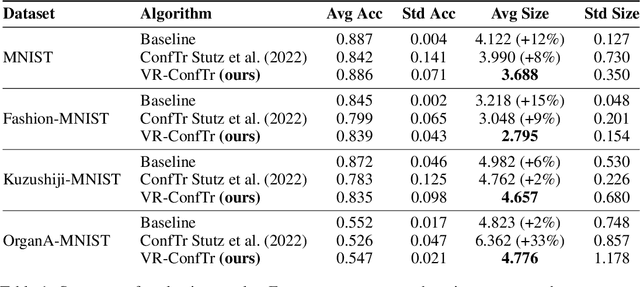
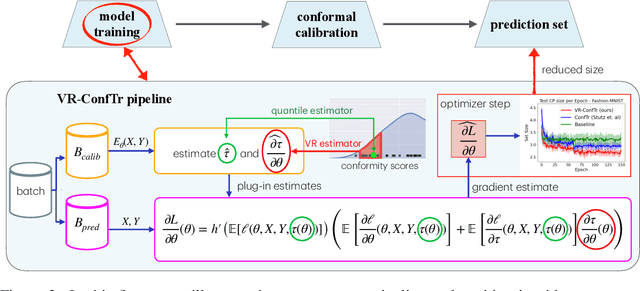
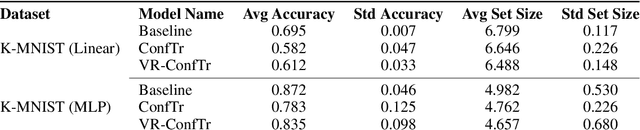
Conformal prediction (CP) is a distribution-free framework for achieving probabilistic guarantees on black-box models. CP is generally applied to a model post-training. Recent research efforts, on the other hand, have focused on optimizing CP efficiency during training. We formalize this concept as the problem of conformal risk minimization (CRM). In this direction, conformal training (ConfTr) by Stutz et al.(2022) is a technique that seeks to minimize the expected prediction set size of a model by simulating CP in-between training updates. Despite its potential, we identify a strong source of sample inefficiency in ConfTr that leads to overly noisy estimated gradients, introducing training instability and limiting practical use. To address this challenge, we propose variance-reduced conformal training (VR-ConfTr), a CRM method that incorporates a variance reduction technique in the gradient estimation of the ConfTr objective function. Through extensive experiments on various benchmark datasets, we demonstrate that VR-ConfTr consistently achieves faster convergence and smaller prediction sets compared to baselines.

DASA: Delay-Adaptive Multi-Agent Stochastic Approximation

We consider a setting in which $N$ agents aim to speedup a common Stochastic Approximation (SA) problem by acting in parallel and communicating with a central server. We assume that the up-link transmissions to the server are subject to asynchronous and potentially unbounded time-varying delays. To mitigate the effect of delays and stragglers while reaping the benefits of distributed computation, we propose \texttt{DASA}, a Delay-Adaptive algorithm for multi-agent Stochastic Approximation. We provide a finite-time analysis of \texttt{DASA} assuming that the agents' stochastic observation processes are independent Markov chains. Significantly advancing existing results, \texttt{DASA} is the first algorithm whose convergence rate depends only on the mixing time $\tau_{mix}$ and on the average delay $\tau_{avg}$ while jointly achieving an $N$-fold convergence speedup under Markovian sampling. Our work is relevant for various SA applications, including multi-agent and distributed temporal difference (TD) learning, Q-learning and stochastic optimization with correlated data.

Stochastic Approximation with Delayed Updates: Finite-Time Rates under Markovian Sampling

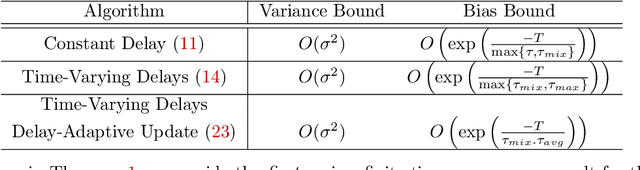
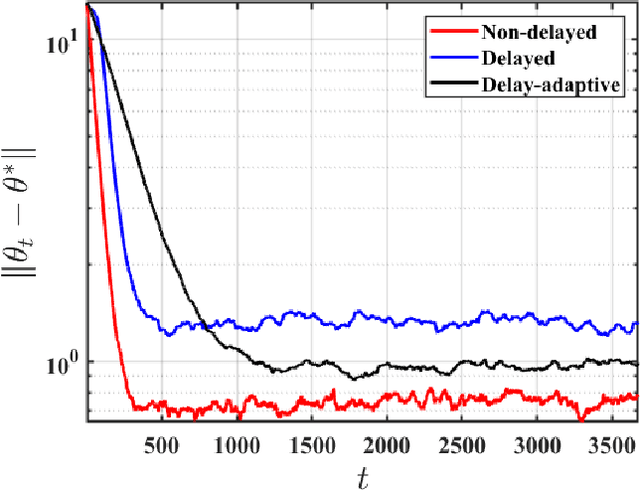
Motivated by applications in large-scale and multi-agent reinforcement learning, we study the non-asymptotic performance of stochastic approximation (SA) schemes with delayed updates under Markovian sampling. While the effect of delays has been extensively studied for optimization, the manner in which they interact with the underlying Markov process to shape the finite-time performance of SA remains poorly understood. In this context, our first main contribution is to show that under time-varying bounded delays, the delayed SA update rule guarantees exponentially fast convergence of the \emph{last iterate} to a ball around the SA operator's fixed point. Notably, our bound is \emph{tight} in its dependence on both the maximum delay $\tau_{max}$, and the mixing time $\tau_{mix}$. To achieve this tight bound, we develop a novel inductive proof technique that, unlike various existing delayed-optimization analyses, relies on establishing uniform boundedness of the iterates. As such, our proof may be of independent interest. Next, to mitigate the impact of the maximum delay on the convergence rate, we provide the first finite-time analysis of a delay-adaptive SA scheme under Markovian sampling. In particular, we show that the exponent of convergence of this scheme gets scaled down by $\tau_{avg}$, as opposed to $\tau_{max}$ for the vanilla delayed SA rule; here, $\tau_{avg}$ denotes the average delay across all iterations. Moreover, the adaptive scheme requires no prior knowledge of the delay sequence for step-size tuning. Our theoretical findings shed light on the finite-time effects of delays for a broad class of algorithms, including TD learning, Q-learning, and stochastic gradient descent under Markovian sampling.