Conformal Risk Minimization with Variance Reduction

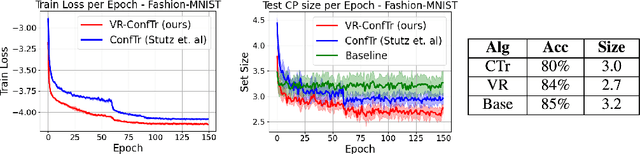
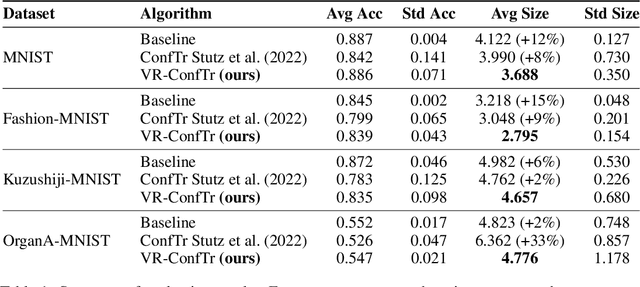
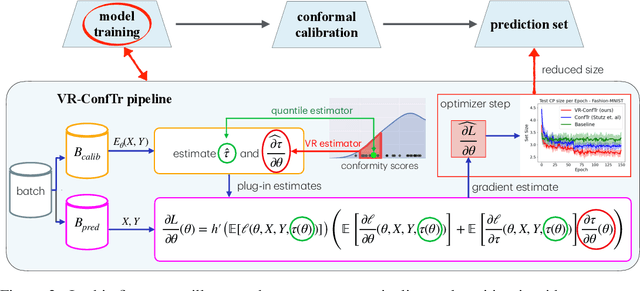
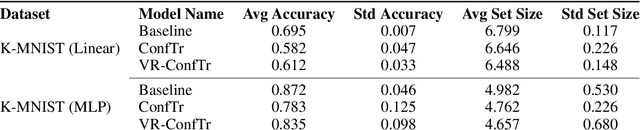
Conformal prediction (CP) is a distribution-free framework for achieving probabilistic guarantees on black-box models. CP is generally applied to a model post-training. Recent research efforts, on the other hand, have focused on optimizing CP efficiency during training. We formalize this concept as the problem of conformal risk minimization (CRM). In this direction, conformal training (ConfTr) by Stutz et al.(2022) is a technique that seeks to minimize the expected prediction set size of a model by simulating CP in-between training updates. Despite its potential, we identify a strong source of sample inefficiency in ConfTr that leads to overly noisy estimated gradients, introducing training instability and limiting practical use. To address this challenge, we propose variance-reduced conformal training (VR-ConfTr), a CRM method that incorporates a variance reduction technique in the gradient estimation of the ConfTr objective function. Through extensive experiments on various benchmark datasets, we demonstrate that VR-ConfTr consistently achieves faster convergence and smaller prediction sets compared to baselines.

Optimizing Deep Neural Networks via Discretization of Finite-Time Convergent Flows

In this paper, we investigate in the context of deep neural networks, the performance of several discretization algorithms for two first-order finite-time optimization flows. These flows are, namely, the rescaled-gradient flow (RGF) and the signed-gradient flow (SGF), and consist of non-Lipscthiz or discontinuous dynamical systems that converge locally in finite time to the minima of gradient-dominated functions. We introduce three discretization methods for these first-order finite-time flows, and provide convergence guarantees. We then apply the proposed algorithms in training neural networks and empirically test their performances on three standard datasets, namely, CIFAR10, SVHN, and MNIST. Our results show that our schemes demonstrate faster convergences against standard optimization alternatives, while achieving equivalent or better accuracy.

A Dynamical Systems Approach for Convergence of the Bayesian EM Algorithm

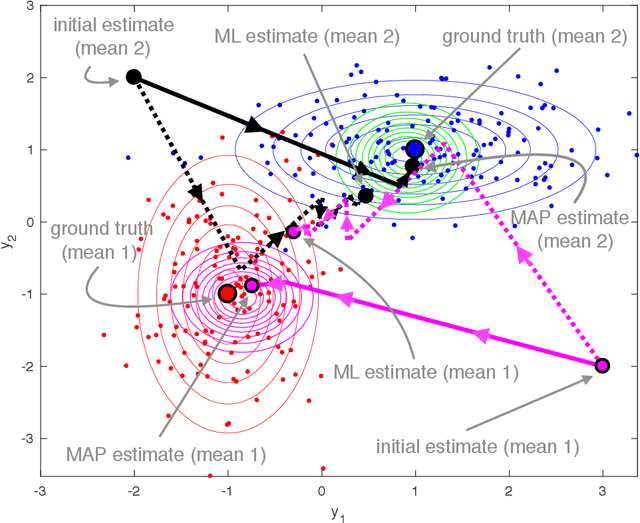
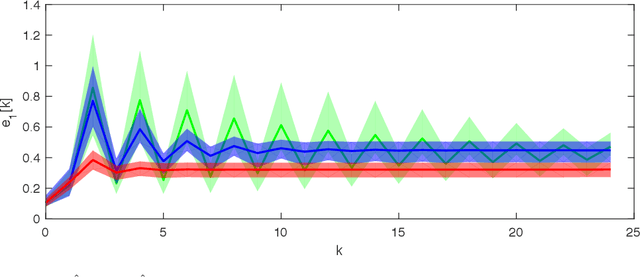
Out of the recent advances in systems and control (S\&C)-based analysis of optimization algorithms, not enough work has been specifically dedicated to machine learning (ML) algorithms and its applications. This paper addresses this gap by illustrating how (discrete-time) Lyapunov stability theory can serve as a powerful tool to aid, or even lead, in the analysis (and potential design) of optimization algorithms that are not necessarily gradient-based. The particular ML problem that this paper focuses on is that of parameter estimation in an incomplete-data Bayesian framework via the popular optimization algorithm known as maximum a posteriori expectation-maximization (MAP-EM). Following first principles from dynamical systems stability theory, conditions for convergence of MAP-EM are developed. Furthermore, if additional assumptions are met, we show that fast convergence (linear or quadratic) is achieved, which could have been difficult to unveil without our adopted S\&C approach. The convergence guarantees in this paper effectively expand the set of sufficient conditions for EM applications, thereby demonstrating the potential of similar S\&C-based convergence analysis of other ML algorithms.

Finite-Time Convergence of Continuous-Time Optimization Algorithms via Differential Inclusions

In this paper, we propose two discontinuous dynamical systems in continuous time with guaranteed prescribed finite-time local convergence to strict local minima of a given cost function. Our approach consists of exploiting a Lyapunov-based differential inequality for differential inclusions, which leads to finite-time stability and thus finite-time convergence with a provable bound on the settling time. In particular, for exact solutions to the aforementioned differential inequality, the settling-time bound is also exact, thus achieving prescribed finite-time convergence. We thus construct a class of discontinuous dynamical systems, of second order with respect to the cost function, that serve as continuous-time optimization algorithms with finite-time convergence and prescribed convergence time. Finally, we illustrate our results on the Rosenbrock function.

Analysis of Gradient-Based Expectation-Maximization-Like Algorithms via Integral Quadratic Constraints

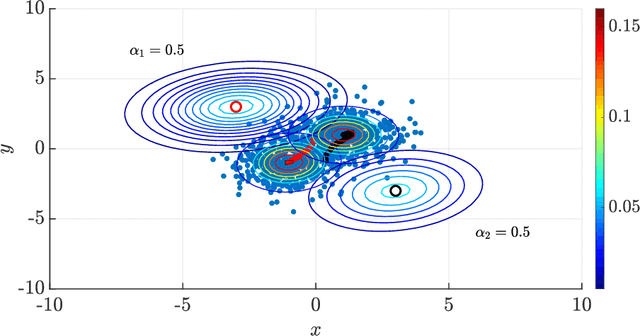
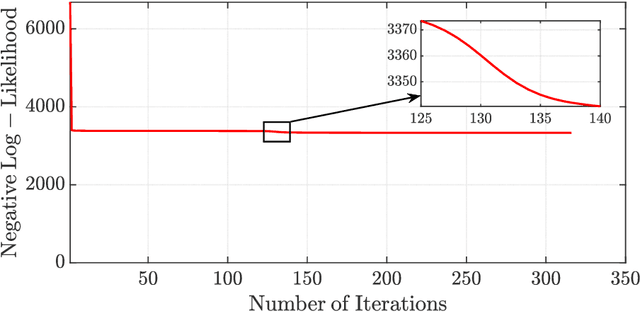
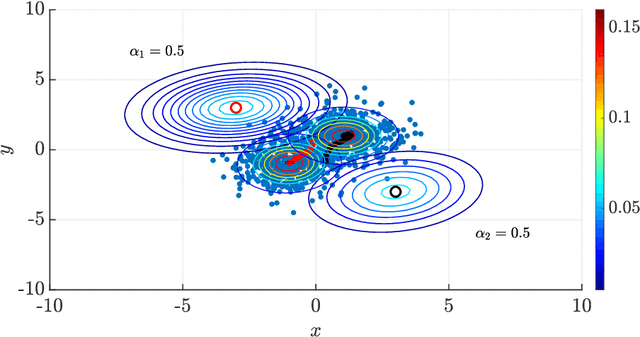
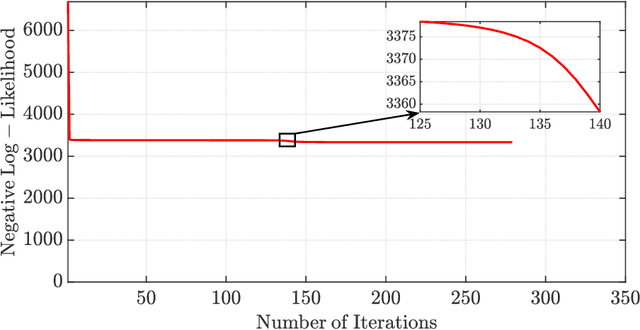
The Expectation-Maximization (EM) algorithm is one of the most popular methods used to solve the problem of distribution-based clustering in unsupervised learning. In this paper, we propose an analysis of a generalized EM (GEM) algorithm and a designed EM-like algorithm, as linear time-invariant (LTI) systems with a feedback nonlinearity, and by leveraging tools from robust control theory, particularly integral quadratic constraints (IQCs). Towards this goal, we investigate the absolute stability of dynamical systems of the above form with a sector-bounded feedback nonlinearity, that represent the aforementioned algorithms. This analysis allows us to craft a strongly convex objective function, which led to the design of the aforementioned novel EM-like algorithm for Gaussian mixture models (GMMs). Furthermore, it allows us to establish bounds on the convergence rates of the studied algorithms. In particular, the derived bounds for our proposed EM-like algorithm generalize bounds found in the literature for the EM algorithm on GMMs, and our analysis of an existing gradient ascent GEM algorithm based on the $Q$-function allowed us to approximately recover bounds found in the literature.

Convergence of the Expectation-Maximization Algorithm Through Discrete-Time Lyapunov Stability Theory

In this paper, we propose a dynamical systems perspective of the Expectation-Maximization (EM) algorithm. More precisely, we can analyze the EM algorithm as a nonlinear state-space dynamical system. The EM algorithm is widely adopted for data clustering and density estimation in statistics, control systems, and machine learning. This algorithm belongs to a large class of iterative algorithms known as proximal point methods. In particular, we re-interpret limit points of the EM algorithm and other local maximizers of the likelihood function it seeks to optimize as equilibria in its dynamical system representation. Furthermore, we propose to assess its convergence as asymptotic stability in the sense of Lyapunov. As a consequence, we proceed by leveraging recent results regarding discrete-time Lyapunov stability theory in order to establish asymptotic stability (and thus, convergence) in the dynamical system representation of the EM algorithm.