GRAM: Generalization in Deep RL with a Robust Adaptation Module

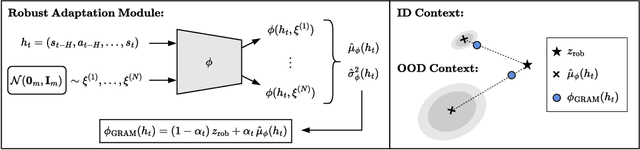
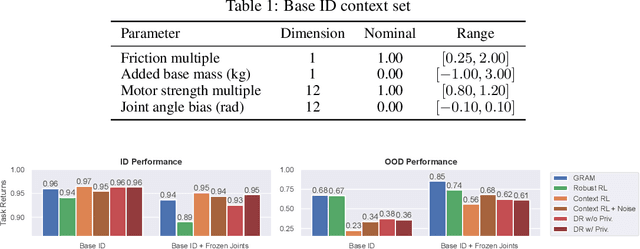
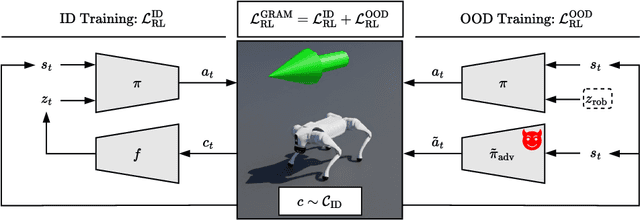
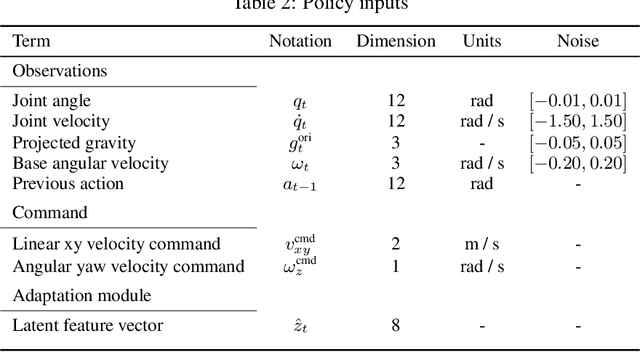
The reliable deployment of deep reinforcement learning in real-world settings requires the ability to generalize across a variety of conditions, including both in-distribution scenarios seen during training as well as novel out-of-distribution scenarios. In this work, we present a framework for dynamics generalization in deep reinforcement learning that unifies these two distinct types of generalization within a single architecture. We introduce a robust adaptation module that provides a mechanism for identifying and reacting to both in-distribution and out-of-distribution environment dynamics, along with a joint training pipeline that combines the goals of in-distribution adaptation and out-of-distribution robustness. Our algorithm GRAM achieves strong generalization performance across in-distribution and out-of-distribution scenarios upon deployment, which we demonstrate on a variety of realistic simulated locomotion tasks with a quadruped robot.

Policy Optimization for PDE Control with a Warm Start

Dimensionality reduction is crucial for controlling nonlinear partial differential equations (PDE) through a "reduce-then-design" strategy, which identifies a reduced-order model and then implements model-based control solutions. However, inaccuracies in the reduced-order modeling can substantially degrade controller performance, especially in PDEs with chaotic behavior. To address this issue, we augment the reduce-then-design procedure with a policy optimization (PO) step. The PO step fine-tunes the model-based controller to compensate for the modeling error from dimensionality reduction. This augmentation shifts the overall strategy into reduce-then-design-then-adapt, where the model-based controller serves as a warm start for PO. Specifically, we study the state-feedback tracking control of PDEs that aims to align the PDE state with a specific constant target subject to a linear-quadratic cost. Through extensive experiments, we show that a few iterations of PO can significantly improve the model-based controller performance. Our approach offers a cost-effective alternative to PDE control using end-to-end reinforcement learning.

Smooth and Sparse Latent Dynamics in Operator Learning with Jerk Regularization

Spatiotemporal modeling is critical for understanding complex systems across various scientific and engineering disciplines, but governing equations are often not fully known or computationally intractable due to inherent system complexity. Data-driven reduced-order models (ROMs) offer a promising approach for fast and accurate spatiotemporal forecasting by computing solutions in a compressed latent space. However, these models often neglect temporal correlations between consecutive snapshots when constructing the latent space, leading to suboptimal compression, jagged latent trajectories, and limited extrapolation ability over time. To address these issues, this paper introduces a continuous operator learning framework that incorporates jerk regularization into the learning of the compressed latent space. This jerk regularization promotes smoothness and sparsity of latent space dynamics, which not only yields enhanced accuracy and convergence speed but also helps identify intrinsic latent space coordinates. Consisting of an implicit neural representation (INR)-based autoencoder and a neural ODE latent dynamics model, the framework allows for inference at any desired spatial or temporal resolution. The effectiveness of this framework is demonstrated through a two-dimensional unsteady flow problem governed by the Navier-Stokes equations, highlighting its potential to expedite high-fidelity simulations in various scientific and engineering applications.

Controlgym: Large-Scale Safety-Critical Control Environments for Benchmarking Reinforcement Learning Algorithms

We introduce controlgym, a library of thirty-six safety-critical industrial control settings, and ten infinite-dimensional partial differential equation (PDE)-based control problems. Integrated within the OpenAI Gym/Gymnasium (Gym) framework, controlgym allows direct applications of standard reinforcement learning (RL) algorithms like stable-baselines3. Our control environments complement those in Gym with continuous, unbounded action and observation spaces, motivated by real-world control applications. Moreover, the PDE control environments uniquely allow the users to extend the state dimensionality of the system to infinity while preserving the intrinsic dynamics. This feature is crucial for evaluating the scalability of RL algorithms for control. This project serves the learning for dynamics & control (L4DC) community, aiming to explore key questions: the convergence of RL algorithms in learning control policies; the stability and robustness issues of learning-based controllers; and the scalability of RL algorithms to high- and potentially infinite-dimensional systems. We open-source the controlgym project at https://github.com/xiangyuan-zhang/controlgym.

Global Convergence of Receding-Horizon Policy Search in Learning Estimator Designs

We introduce the receding-horizon policy gradient (RHPG) algorithm, the first PG algorithm with provable global convergence in learning the optimal linear estimator designs, i.e., the Kalman filter (KF). Notably, the RHPG algorithm does not require any prior knowledge of the system for initialization and does not require the target system to be open-loop stable. The key of RHPG is that we integrate vanilla PG (or any other policy search directions) into a dynamic programming outer loop, which iteratively decomposes the infinite-horizon KF problem that is constrained and non-convex in the policy parameter into a sequence of static estimation problems that are unconstrained and strongly-convex, thus enabling global convergence. We further provide fine-grained analyses of the optimization landscape under RHPG and detail the convergence and sample complexity guarantees of the algorithm. This work serves as an initial attempt to develop reinforcement learning algorithms specifically for control applications with performance guarantees by utilizing classic control theory in both algorithmic design and theoretical analyses. Lastly, we validate our theories by deploying the RHPG algorithm to learn the Kalman filter design of a large-scale convection-diffusion model. We open-source the code repository at \url{https://github.com/xiangyuan-zhang/LearningKF}.

Risk-Averse Model Uncertainty for Distributionally Robust Safe Reinforcement Learning

Many real-world domains require safe decision making in the presence of uncertainty. In this work, we propose a deep reinforcement learning framework for approaching this important problem. We consider a risk-averse perspective towards model uncertainty through the use of coherent distortion risk measures, and we show that our formulation is equivalent to a distributionally robust safe reinforcement learning problem with robustness guarantees on performance and safety. We propose an efficient implementation that only requires access to a single training environment, and we demonstrate that our framework produces robust, safe performance on a variety of continuous control tasks with safety constraints in the Real-World Reinforcement Learning Suite.

Domain Knowledge-Infused Deep Learning for Automated Analog/Radio-Frequency Circuit Parameter Optimization

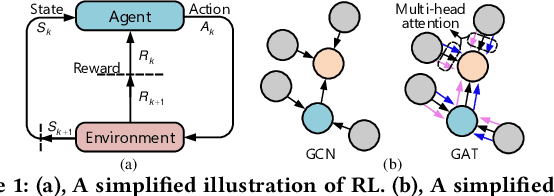
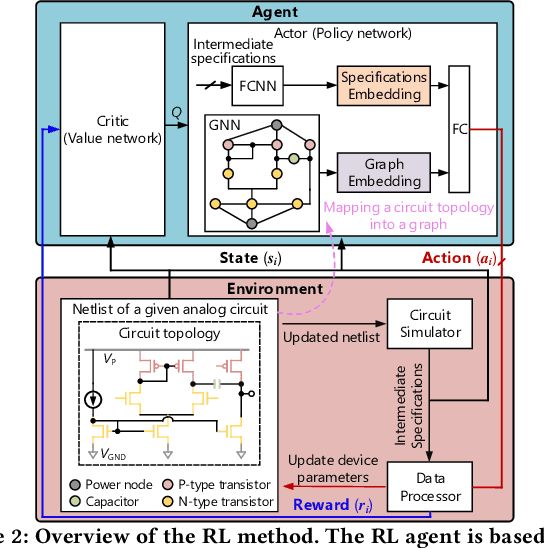
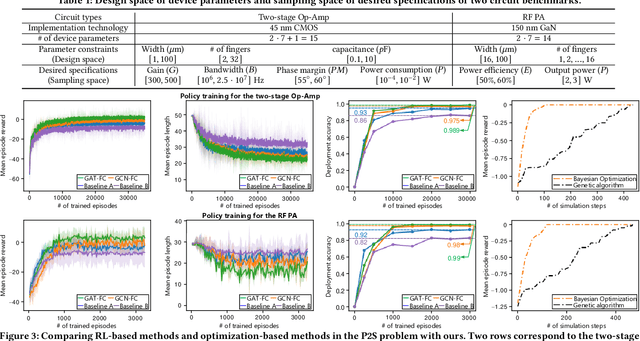
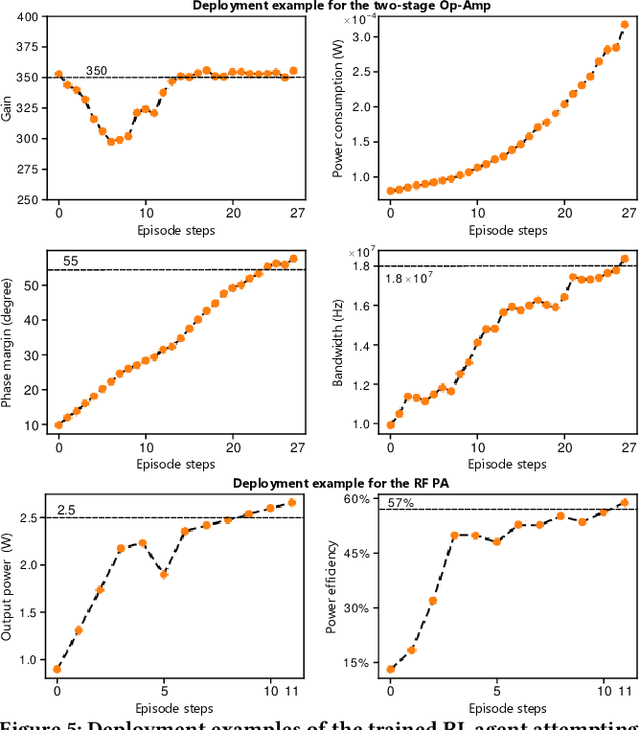
The design automation of analog circuits is a longstanding challenge. This paper presents a reinforcement learning method enhanced by graph learning to automate the analog circuit parameter optimization at the pre-layout stage, i.e., finding device parameters to fulfill desired circuit specifications. Unlike all prior methods, our approach is inspired by human experts who rely on domain knowledge of analog circuit design (e.g., circuit topology and couplings between circuit specifications) to tackle the problem. By originally incorporating such key domain knowledge into policy training with a multimodal network, the method best learns the complex relations between circuit parameters and design targets, enabling optimal decisions in the optimization process. Experimental results on exemplary circuits show it achieves human-level design accuracy (99%) 1.5X efficiency of existing best-performing methods. Our method also shows better generalization ability to unseen specifications and optimality in circuit performance optimization. Moreover, it applies to design radio-frequency circuits on emerging semiconductor technologies, breaking the limitations of prior learning methods in designing conventional analog circuits.

Domain Knowledge-Based Automated Analog Circuit Design with Deep Reinforcement Learning

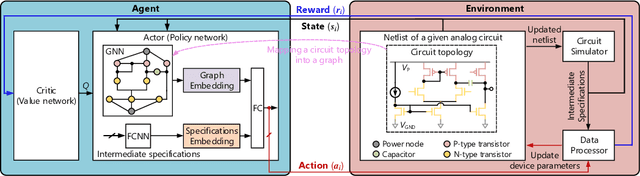
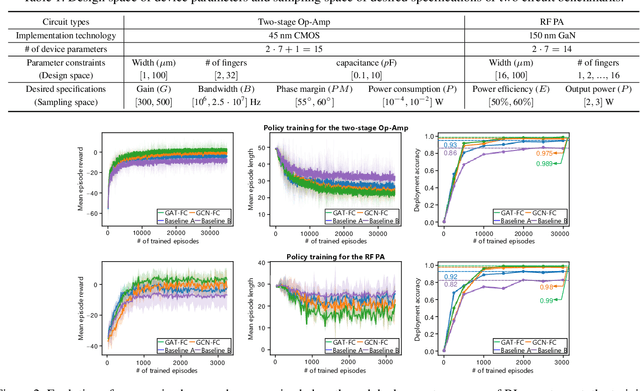
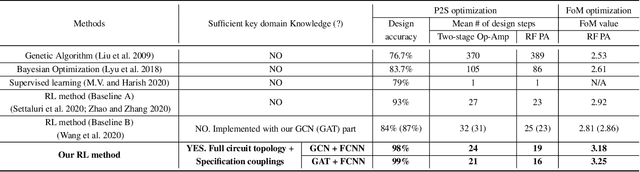
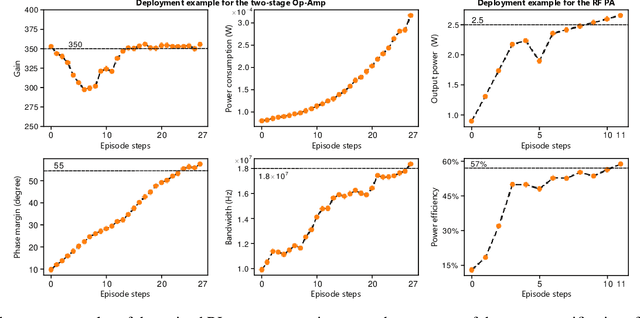
The design automation of analog circuits is a longstanding challenge in the integrated circuit field. This paper presents a deep reinforcement learning method to expedite the design of analog circuits at the pre-layout stage, where the goal is to find device parameters to fulfill desired circuit specifications. Our approach is inspired by experienced human designers who rely on domain knowledge of analog circuit design (e.g., circuit topology and couplings between circuit specifications) to tackle the problem. Unlike all prior methods, our method originally incorporates such key domain knowledge into policy learning with a graph-based policy network, thereby best modeling the relations between circuit parameters and design targets. Experimental results on exemplary circuits show it achieves human-level design accuracy (~99%) with 1.5x efficiency of existing best-performing methods. Our method also shows better generalization ability to unseen specifications and optimality in circuit performance optimization. Moreover, it applies to designing diverse analog circuits across different semiconductor technologies, breaking the limitations of prior ad-hoc methods in designing one particular type of analog circuits with conventional semiconductor technology.

Lyapunov Robust Constrained-MDPs: Soft-Constrained Robustly Stable Policy Optimization under Model Uncertainty

Safety and robustness are two desired properties for any reinforcement learning algorithm. CMDPs can handle additional safety constraints and RMDPs can perform well under model uncertainties. In this paper, we propose to unite these two frameworks resulting in robust constrained MDPs (RCMDPs). The motivation is to develop a framework that can satisfy safety constraints while also simultaneously offer robustness to model uncertainties. We develop the RCMDP objective, derive gradient update formula to optimize this objective and then propose policy gradient based algorithms. We also independently propose Lyapunov based reward shaping for RCMDPs, yielding better stability and convergence properties.

Robust Constrained-MDPs: Soft-Constrained Robust Policy Optimization under Model Uncertainty

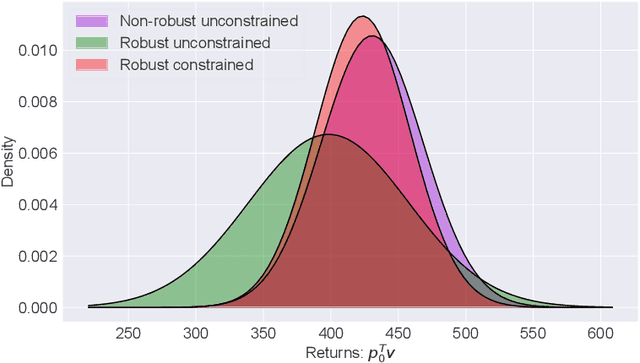
In this paper, we focus on the problem of robustifying reinforcement learning (RL) algorithms with respect to model uncertainties. Indeed, in the framework of model-based RL, we propose to merge the theory of constrained Markov decision process (CMDP), with the theory of robust Markov decision process (RMDP), leading to a formulation of robust constrained-MDPs (RCMDP). This formulation, simple in essence, allows us to design RL algorithms that are robust in performance, and provides constraint satisfaction guarantees, with respect to uncertainties in the system's states transition probabilities. The need for RCMPDs is important for real-life applications of RL. For instance, such formulation can play an important role for policy transfer from simulation to real world (Sim2Real) in safety critical applications, which would benefit from performance and safety guarantees which are robust w.r.t model uncertainty. We first propose the general problem formulation under the concept of RCMDP, and then propose a Lagrangian formulation of the optimal problem, leading to a robust-constrained policy gradient RL algorithm. We finally validate this concept on the inventory management problem.