Lyapunov Robust Constrained-MDPs: Soft-Constrained Robustly Stable Policy Optimization under Model Uncertainty

Safety and robustness are two desired properties for any reinforcement learning algorithm. CMDPs can handle additional safety constraints and RMDPs can perform well under model uncertainties. In this paper, we propose to unite these two frameworks resulting in robust constrained MDPs (RCMDPs). The motivation is to develop a framework that can satisfy safety constraints while also simultaneously offer robustness to model uncertainties. We develop the RCMDP objective, derive gradient update formula to optimize this objective and then propose policy gradient based algorithms. We also independently propose Lyapunov based reward shaping for RCMDPs, yielding better stability and convergence properties.

Robust Constrained-MDPs: Soft-Constrained Robust Policy Optimization under Model Uncertainty

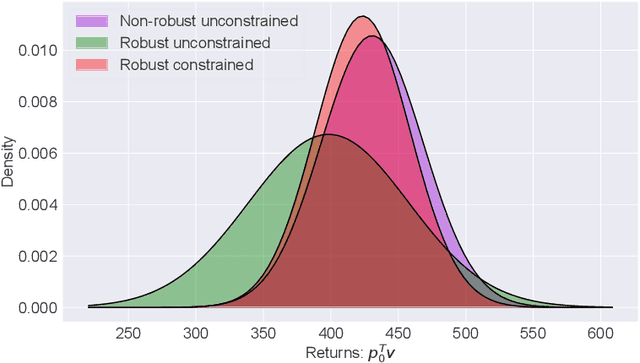
In this paper, we focus on the problem of robustifying reinforcement learning (RL) algorithms with respect to model uncertainties. Indeed, in the framework of model-based RL, we propose to merge the theory of constrained Markov decision process (CMDP), with the theory of robust Markov decision process (RMDP), leading to a formulation of robust constrained-MDPs (RCMDP). This formulation, simple in essence, allows us to design RL algorithms that are robust in performance, and provides constraint satisfaction guarantees, with respect to uncertainties in the system's states transition probabilities. The need for RCMPDs is important for real-life applications of RL. For instance, such formulation can play an important role for policy transfer from simulation to real world (Sim2Real) in safety critical applications, which would benefit from performance and safety guarantees which are robust w.r.t model uncertainty. We first propose the general problem formulation under the concept of RCMDP, and then propose a Lagrangian formulation of the optimal problem, leading to a robust-constrained policy gradient RL algorithm. We finally validate this concept on the inventory management problem.

Entropic Risk Constrained Soft-Robust Policy Optimization

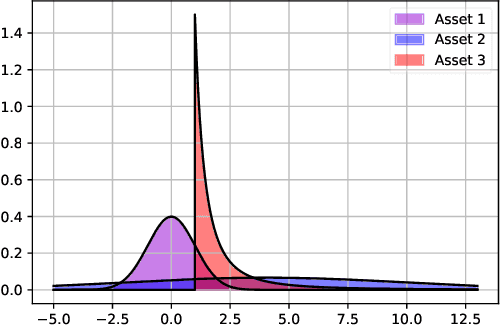
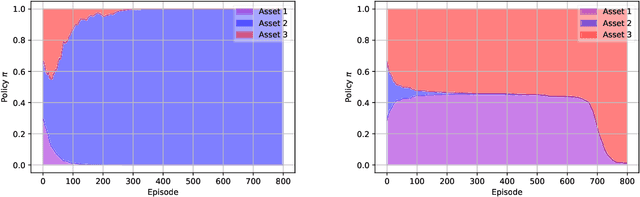
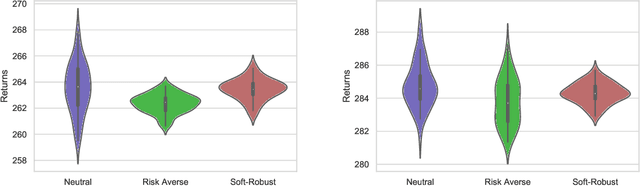
Having a perfect model to compute the optimal policy is often infeasible in reinforcement learning. It is important in high-stakes domains to quantify and manage risk induced by model uncertainties. Entropic risk measure is an exponential utility-based convex risk measure that satisfies many reasonable properties. In this paper, we propose an entropic risk constrained policy gradient and actor-critic algorithms that are risk-averse to the model uncertainty. We demonstrate the usefulness of our algorithms on several problem domains.

A Probabilistic Approach to Satisfiability of Propositional Logic Formulae

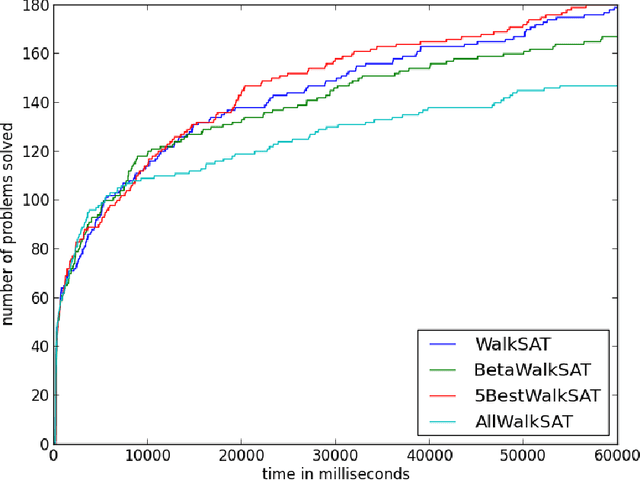
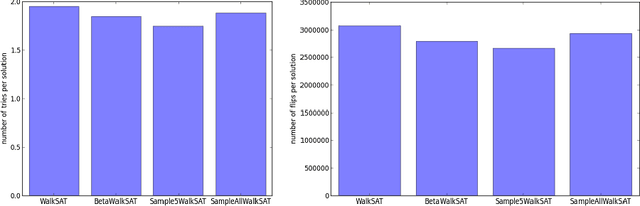
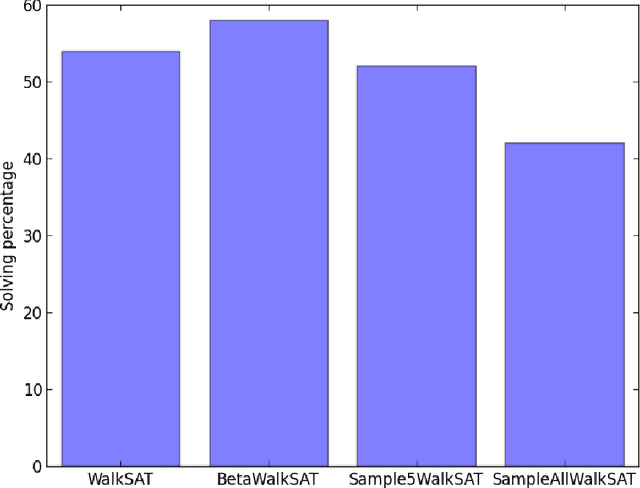
We propose a version of WalkSAT algorithm, named as BetaWalkSAT. This method uses probabilistic reasoning for biasing the starting state of the local search algorithm. Beta distribution is used to model the belief over boolean values of the literals. Our results suggest that, the proposed BetaWalkSAT algorithm can outperform other uninformed local search approaches for complex boolean satisfiability problems.

Optimizing Norm-Bounded Weighted Ambiguity Sets for Robust MDPs

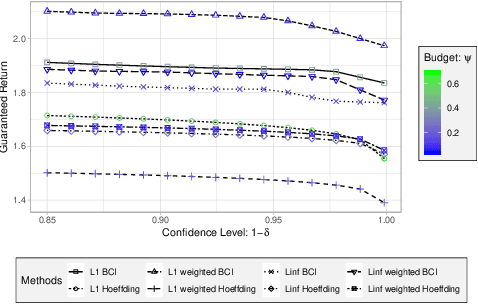
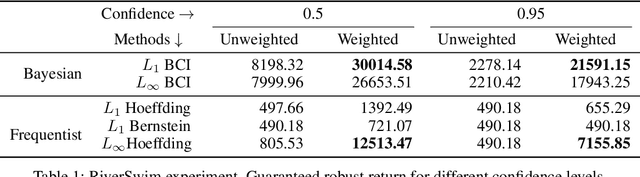
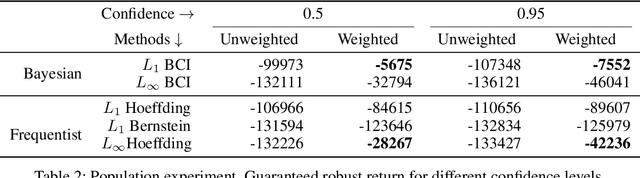
Optimal policies in Markov decision processes (MDPs) are very sensitive to model misspecification. This raises serious concerns about deploying them in high-stake domains. Robust MDPs (RMDP) provide a promising framework to mitigate vulnerabilities by computing policies with worst-case guarantees in reinforcement learning. The solution quality of an RMDP depends on the ambiguity set, which is a quantification of model uncertainties. In this paper, we propose a new approach for optimizing the shape of the ambiguity sets for RMDPs. Our method departs from the conventional idea of constructing a norm-bounded uniform and symmetric ambiguity set. We instead argue that the structure of a near-optimal ambiguity set is problem specific. Our proposed method computes a weight parameter from the value functions, and these weights then drive the shape of the ambiguity sets. Our theoretical analysis demonstrates the rationale of the proposed idea. We apply our method to several different problem domains, and the empirical results further furnish the practical promise of weighted near-optimal ambiguity sets.

High-Confidence Policy Optimization: Reshaping Ambiguity Sets in Robust MDPs

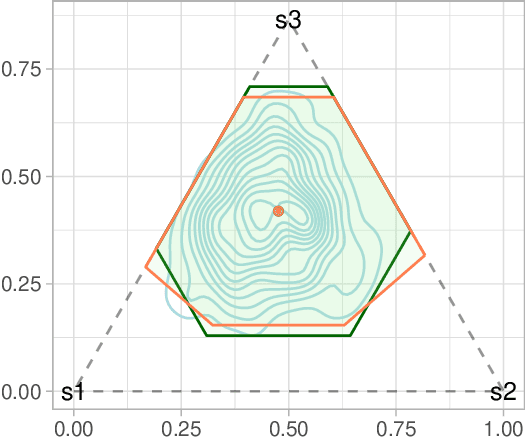
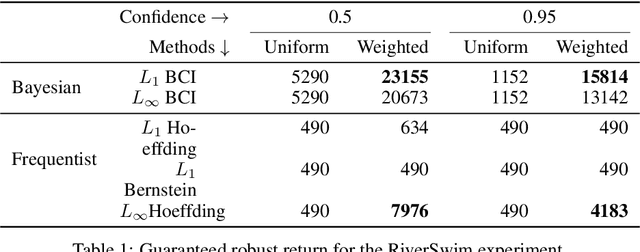
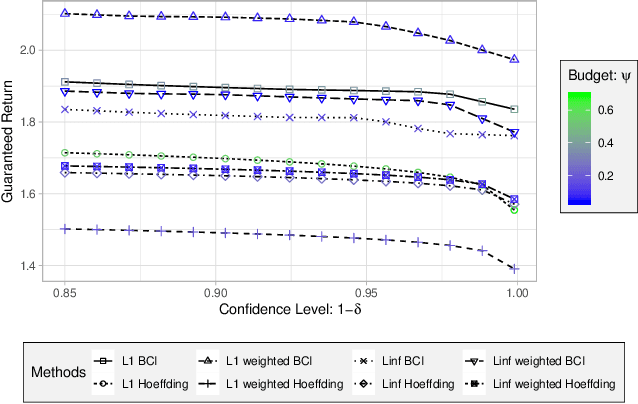
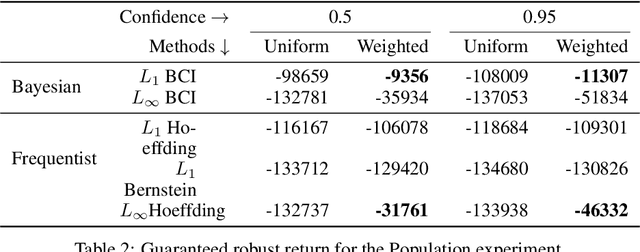
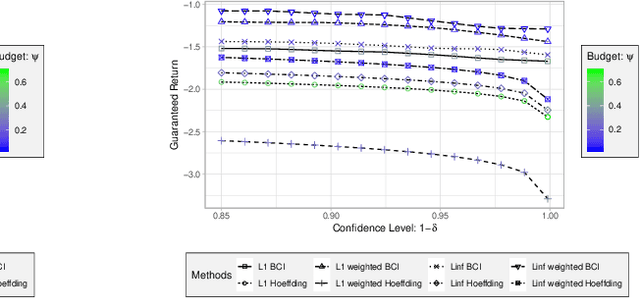
Robust MDPs are a promising framework for computing robust policies in reinforcement learning. Ambiguity sets, which represent the plausible errors in transition probabilities, determine the trade-off between robustness and average-case performance. The standard practice of defining ambiguity sets using the $L_1$ norm leads, unfortunately, to loose and impractical guarantees. This paper describes new methods for optimizing the shape of ambiguity sets beyond the $L_1$ norm. We derive new high-confidence sampling bounds for weighted $L_1$ and weighted $L_\infty$ ambiguity sets and describe how to compute near-optimal weights from rough value function estimates. Experimental results on a diverse set of benchmarks show that optimized ambiguity sets provide significantly tighter robustness guarantees.

A Short Survey on Probabilistic Reinforcement Learning

A reinforcement learning agent tries to maximize its cumulative payoff by interacting in an unknown environment. It is important for the agent to explore suboptimal actions as well as to pick actions with highest known rewards. Yet, in sensitive domains, collecting more data with exploration is not always possible, but it is important to find a policy with a certain performance guaranty. In this paper, we present a brief survey of methods available in the literature for balancing exploration-exploitation trade off and computing robust solutions from fixed samples in reinforcement learning.

Tight Bayesian Ambiguity Sets for Robust MDPs

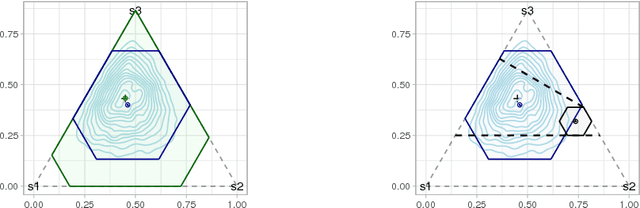
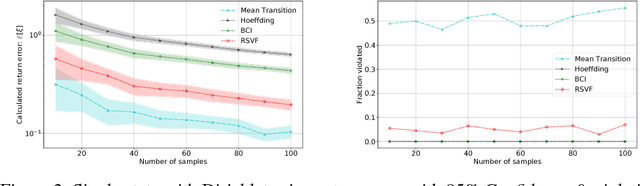
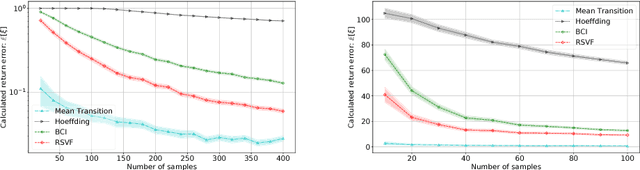
Robustness is important for sequential decision making in a stochastic dynamic environment with uncertain probabilistic parameters. We address the problem of using robust MDPs (RMDPs) to compute policies with provable worst-case guarantees in reinforcement learning. The quality and robustness of an RMDP solution is determined by its ambiguity set. Existing methods construct ambiguity sets that lead to impractically conservative solutions. In this paper, we propose RSVF, which achieves less conservative solutions with the same worst-case guarantees by 1) leveraging a Bayesian prior, 2) optimizing the size and location of the ambiguity set, and, most importantly, 3) relaxing the requirement that the set is a confidence interval. Our theoretical analysis shows the safety of RSVF, and the empirical results demonstrate its practical promise.

Value Directed Exploration in Multi-Armed Bandits with Structured Priors

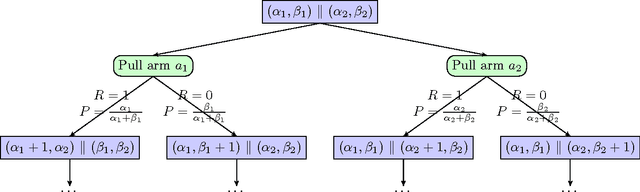
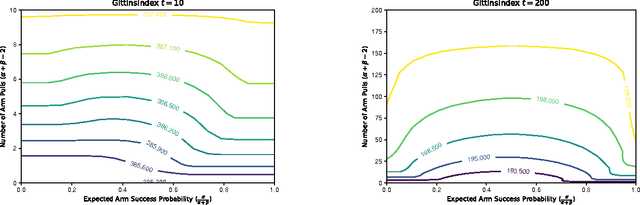
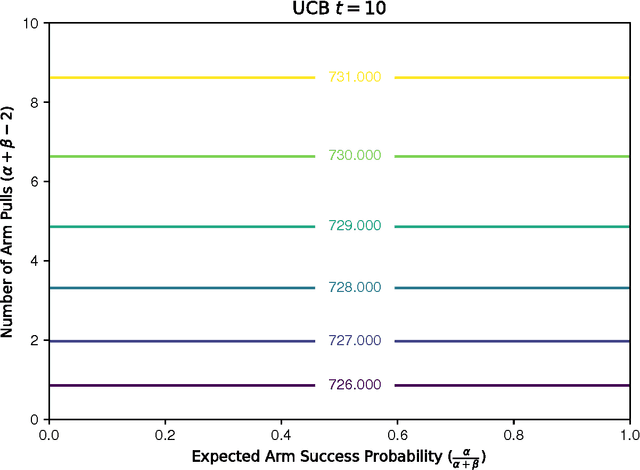
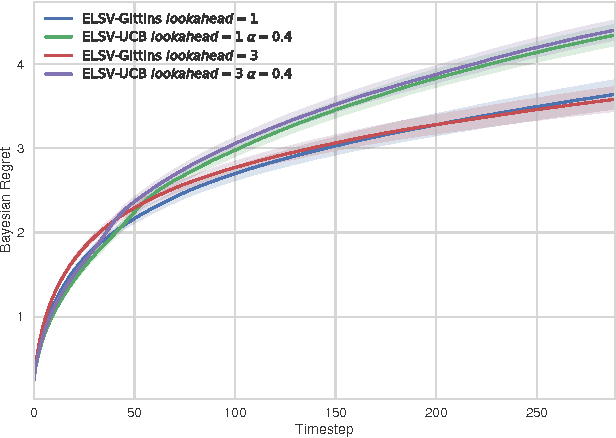
Multi-armed bandits are a quintessential machine learning problem requiring the balancing of exploration and exploitation. While there has been progress in developing algorithms with strong theoretical guarantees, there has been less focus on practical near-optimal finite-time performance. In this paper, we propose an algorithm for Bayesian multi-armed bandits that utilizes value-function-driven online planning techniques. Building on previous work on UCB and Gittins index, we introduce linearly-separable value functions that take both the expected return and the benefit of exploration into consideration to perform n-step lookahead. The algorithm enjoys a sub-linear performance guarantee and we present simulation results that confirm its strength in problems with structured priors. The simplicity and generality of our approach makes it a strong candidate for analyzing more complex multi-armed bandit problems.