Entropic Risk Constrained Soft-Robust Policy Optimization

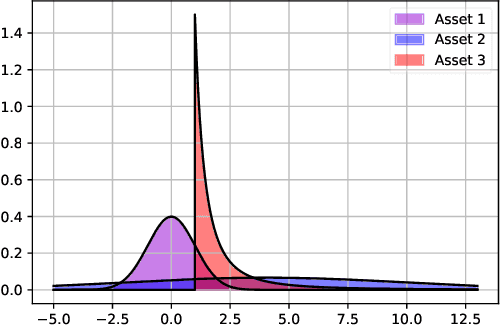
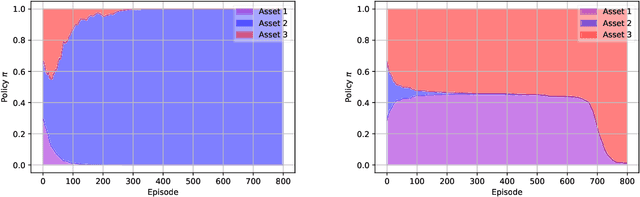
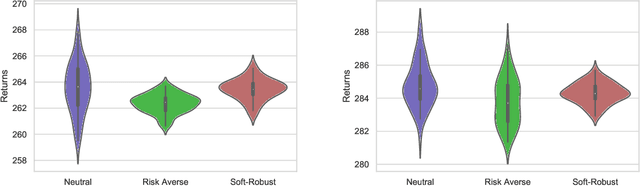
Having a perfect model to compute the optimal policy is often infeasible in reinforcement learning. It is important in high-stakes domains to quantify and manage risk induced by model uncertainties. Entropic risk measure is an exponential utility-based convex risk measure that satisfies many reasonable properties. In this paper, we propose an entropic risk constrained policy gradient and actor-critic algorithms that are risk-averse to the model uncertainty. We demonstrate the usefulness of our algorithms on several problem domains.

Optimizing Norm-Bounded Weighted Ambiguity Sets for Robust MDPs

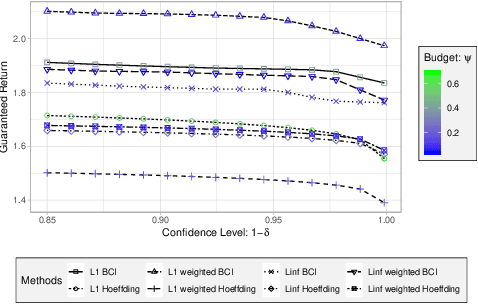
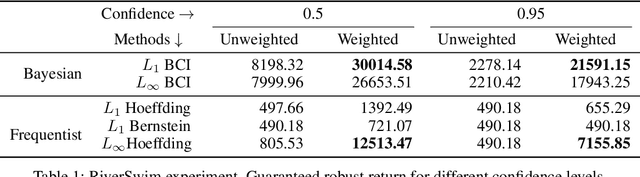
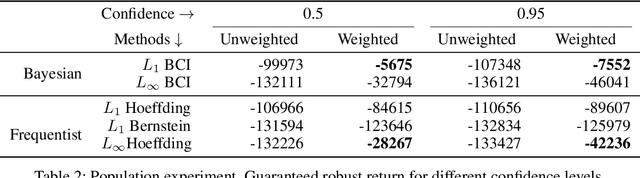
Optimal policies in Markov decision processes (MDPs) are very sensitive to model misspecification. This raises serious concerns about deploying them in high-stake domains. Robust MDPs (RMDP) provide a promising framework to mitigate vulnerabilities by computing policies with worst-case guarantees in reinforcement learning. The solution quality of an RMDP depends on the ambiguity set, which is a quantification of model uncertainties. In this paper, we propose a new approach for optimizing the shape of the ambiguity sets for RMDPs. Our method departs from the conventional idea of constructing a norm-bounded uniform and symmetric ambiguity set. We instead argue that the structure of a near-optimal ambiguity set is problem specific. Our proposed method computes a weight parameter from the value functions, and these weights then drive the shape of the ambiguity sets. Our theoretical analysis demonstrates the rationale of the proposed idea. We apply our method to several different problem domains, and the empirical results further furnish the practical promise of weighted near-optimal ambiguity sets.

High-Confidence Policy Optimization: Reshaping Ambiguity Sets in Robust MDPs

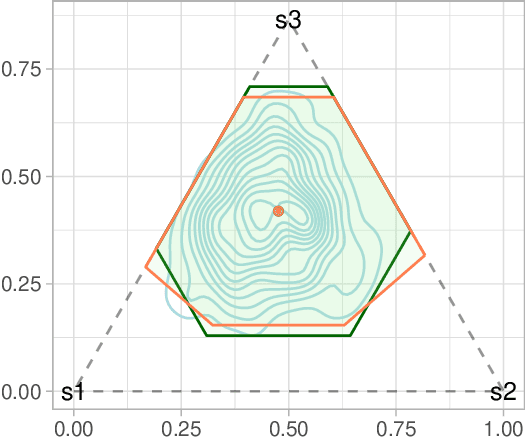
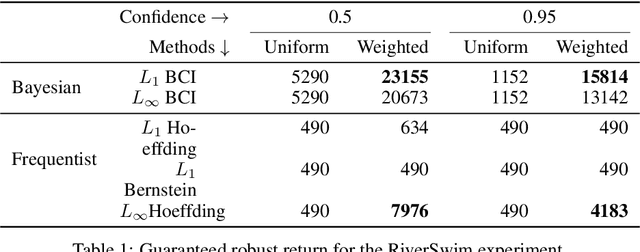
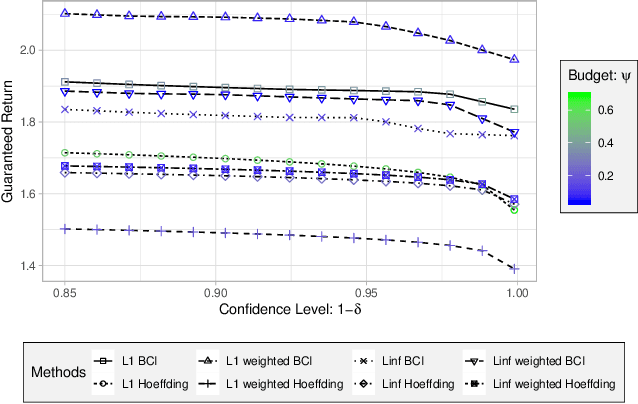
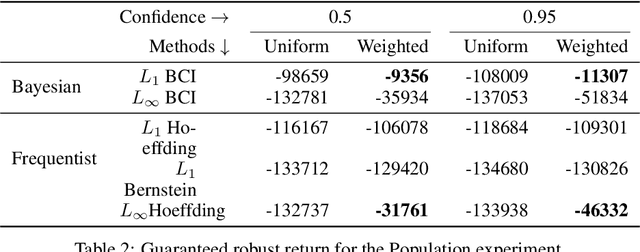
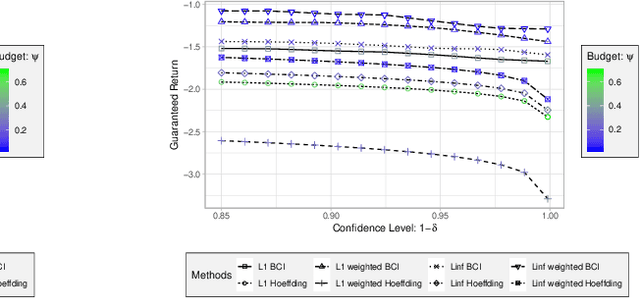
Robust MDPs are a promising framework for computing robust policies in reinforcement learning. Ambiguity sets, which represent the plausible errors in transition probabilities, determine the trade-off between robustness and average-case performance. The standard practice of defining ambiguity sets using the $L_1$ norm leads, unfortunately, to loose and impractical guarantees. This paper describes new methods for optimizing the shape of ambiguity sets beyond the $L_1$ norm. We derive new high-confidence sampling bounds for weighted $L_1$ and weighted $L_\infty$ ambiguity sets and describe how to compute near-optimal weights from rough value function estimates. Experimental results on a diverse set of benchmarks show that optimized ambiguity sets provide significantly tighter robustness guarantees.

Monte Carlo Localization in Hand-Drawn Maps

Robot localization is a one of the most important problems in robotics. Most of the existing approaches assume that the map of the environment is available beforehand and focus on accurate metrical localization. In this paper, we address the localization problem when the map of the environment is not present beforehand, and the robot relies on a hand-drawn map from a non-expert user. We addressed this problem by expressing the robot pose in the pixel coordinate and simultaneously estimate a local deformation of the hand-drawn map. Experiments show that we are able to localize the robot in the correct room with a robustness up to 80%