High-Confidence Policy Optimization: Reshaping Ambiguity Sets in Robust MDPs
Paper and Code
Oct 25, 2019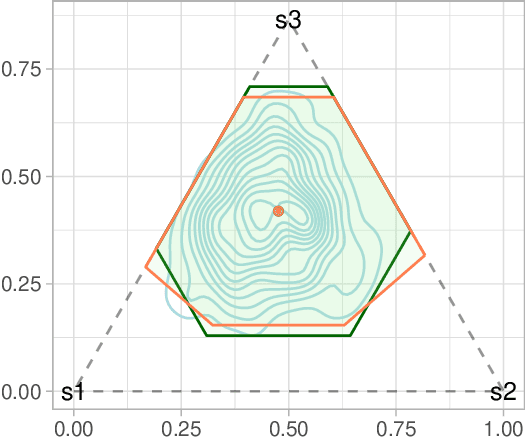
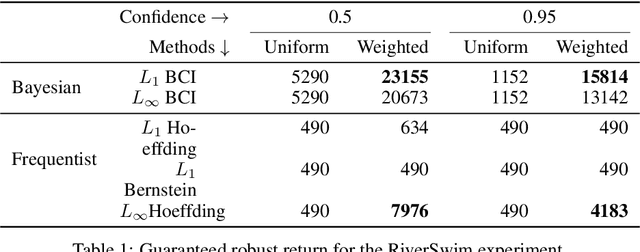
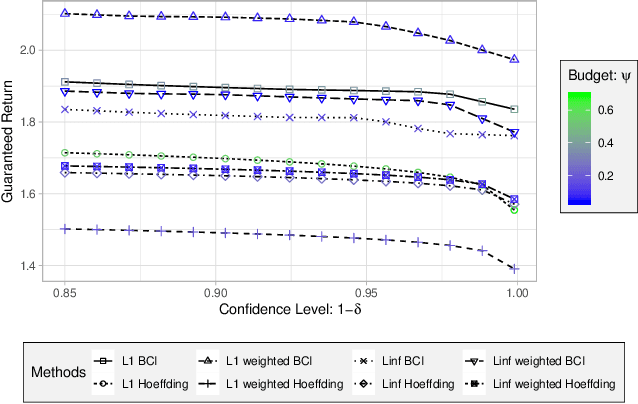
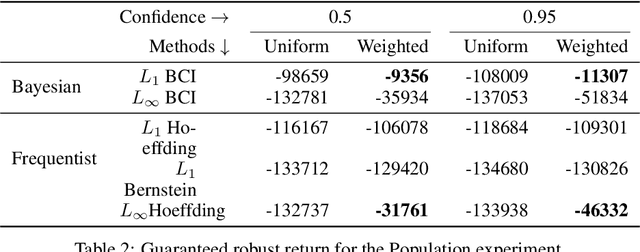
Robust MDPs are a promising framework for computing robust policies in reinforcement learning. Ambiguity sets, which represent the plausible errors in transition probabilities, determine the trade-off between robustness and average-case performance. The standard practice of defining ambiguity sets using the $L_1$ norm leads, unfortunately, to loose and impractical guarantees. This paper describes new methods for optimizing the shape of ambiguity sets beyond the $L_1$ norm. We derive new high-confidence sampling bounds for weighted $L_1$ and weighted $L_\infty$ ambiguity sets and describe how to compute near-optimal weights from rough value function estimates. Experimental results on a diverse set of benchmarks show that optimized ambiguity sets provide significantly tighter robustness guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge