Structure Matters: Dynamic Policy Gradient

In this work, we study $\gamma$-discounted infinite-horizon tabular Markov decision processes (MDPs) and introduce a framework called dynamic policy gradient (DynPG). The framework directly integrates dynamic programming with (any) policy gradient method, explicitly leveraging the Markovian property of the environment. DynPG dynamically adjusts the problem horizon during training, decomposing the original infinite-horizon MDP into a sequence of contextual bandit problems. By iteratively solving these contextual bandits, DynPG converges to the stationary optimal policy of the infinite-horizon MDP. To demonstrate the power of DynPG, we establish its non-asymptotic global convergence rate under the tabular softmax parametrization, focusing on the dependencies on salient but essential parameters of the MDP. By combining classical arguments from dynamic programming with more recent convergence arguments of policy gradient schemes, we prove that softmax DynPG scales polynomially in the effective horizon $(1-\gamma)^{-1}$. Our findings contrast recent exponential lower bound examples for vanilla policy gradient.

Decision Transformer as a Foundation Model for Partially Observable Continuous Control

Closed-loop control of nonlinear dynamical systems with partial-state observability demands expert knowledge of a diverse, less standardized set of theoretical tools. Moreover, it requires a delicate integration of controller and estimator designs to achieve the desired system behavior. To establish a general controller synthesis framework, we explore the Decision Transformer (DT) architecture. Specifically, we first frame the control task as predicting the current optimal action based on past observations, actions, and rewards, eliminating the need for a separate estimator design. Then, we leverage the pre-trained language models, i.e., the Generative Pre-trained Transformer (GPT) series, to initialize DT and subsequently train it for control tasks using low-rank adaptation (LoRA). Our comprehensive experiments across five distinct control tasks, ranging from maneuvering aerospace systems to controlling partial differential equations (PDEs), demonstrate DT's capability to capture the parameter-agnostic structures intrinsic to control tasks. DT exhibits remarkable zero-shot generalization abilities for completely new tasks and rapidly surpasses expert performance levels with a minimal amount of demonstration data. These findings highlight the potential of DT as a foundational controller for general control applications.

Policy Optimization for PDE Control with a Warm Start

Dimensionality reduction is crucial for controlling nonlinear partial differential equations (PDE) through a "reduce-then-design" strategy, which identifies a reduced-order model and then implements model-based control solutions. However, inaccuracies in the reduced-order modeling can substantially degrade controller performance, especially in PDEs with chaotic behavior. To address this issue, we augment the reduce-then-design procedure with a policy optimization (PO) step. The PO step fine-tunes the model-based controller to compensate for the modeling error from dimensionality reduction. This augmentation shifts the overall strategy into reduce-then-design-then-adapt, where the model-based controller serves as a warm start for PO. Specifically, we study the state-feedback tracking control of PDEs that aims to align the PDE state with a specific constant target subject to a linear-quadratic cost. Through extensive experiments, we show that a few iterations of PO can significantly improve the model-based controller performance. Our approach offers a cost-effective alternative to PDE control using end-to-end reinforcement learning.

Controlgym: Large-Scale Safety-Critical Control Environments for Benchmarking Reinforcement Learning Algorithms

We introduce controlgym, a library of thirty-six safety-critical industrial control settings, and ten infinite-dimensional partial differential equation (PDE)-based control problems. Integrated within the OpenAI Gym/Gymnasium (Gym) framework, controlgym allows direct applications of standard reinforcement learning (RL) algorithms like stable-baselines3. Our control environments complement those in Gym with continuous, unbounded action and observation spaces, motivated by real-world control applications. Moreover, the PDE control environments uniquely allow the users to extend the state dimensionality of the system to infinity while preserving the intrinsic dynamics. This feature is crucial for evaluating the scalability of RL algorithms for control. This project serves the learning for dynamics & control (L4DC) community, aiming to explore key questions: the convergence of RL algorithms in learning control policies; the stability and robustness issues of learning-based controllers; and the scalability of RL algorithms to high- and potentially infinite-dimensional systems. We open-source the controlgym project at https://github.com/xiangyuan-zhang/controlgym.

Global Convergence of Receding-Horizon Policy Search in Learning Estimator Designs

We introduce the receding-horizon policy gradient (RHPG) algorithm, the first PG algorithm with provable global convergence in learning the optimal linear estimator designs, i.e., the Kalman filter (KF). Notably, the RHPG algorithm does not require any prior knowledge of the system for initialization and does not require the target system to be open-loop stable. The key of RHPG is that we integrate vanilla PG (or any other policy search directions) into a dynamic programming outer loop, which iteratively decomposes the infinite-horizon KF problem that is constrained and non-convex in the policy parameter into a sequence of static estimation problems that are unconstrained and strongly-convex, thus enabling global convergence. We further provide fine-grained analyses of the optimization landscape under RHPG and detail the convergence and sample complexity guarantees of the algorithm. This work serves as an initial attempt to develop reinforcement learning algorithms specifically for control applications with performance guarantees by utilizing classic control theory in both algorithmic design and theoretical analyses. Lastly, we validate our theories by deploying the RHPG algorithm to learn the Kalman filter design of a large-scale convection-diffusion model. We open-source the code repository at \url{https://github.com/xiangyuan-zhang/LearningKF}.

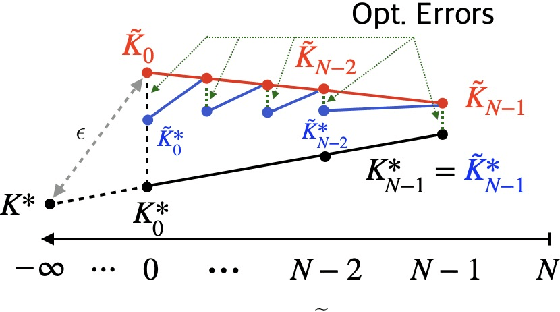
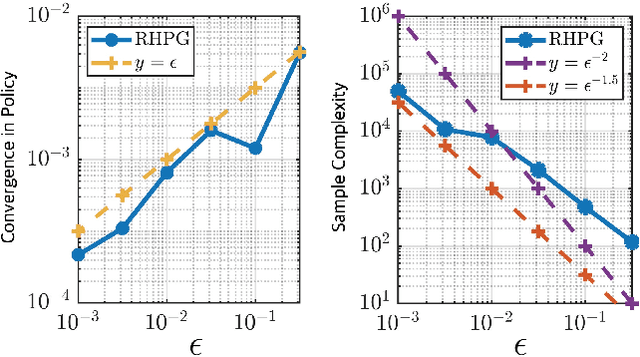
Revisiting LQR Control from the Perspective of Receding-Horizon Policy Gradient

We revisit in this paper the discrete-time linear quadratic regulator (LQR) problem from the perspective of receding-horizon policy gradient (RHPG), a newly developed model-free learning framework for control applications. We provide a fine-grained sample complexity analysis for RHPG to learn a control policy that is both stabilizing and $\epsilon$-close to the optimal LQR solution, and our algorithm does not require knowing a stabilizing control policy for initialization. Combined with the recent application of RHPG in learning the Kalman filter, we demonstrate the general applicability of RHPG in linear control and estimation with streamlined analyses.

Learning the Kalman Filter with Fine-Grained Sample Complexity

We develop the first end-to-end sample complexity of model-free policy gradient (PG) methods in discrete-time infinite-horizon Kalman filtering. Specifically, we introduce the receding-horizon policy gradient (RHPG-KF) framework and demonstrate $\tilde{\mathcal{O}}(\epsilon^{-2})$ sample complexity for RHPG-KF in learning a stabilizing filter that is $\epsilon$-close to the optimal Kalman filter. Notably, the proposed RHPG-KF framework does not require the system to be open-loop stable nor assume any prior knowledge of a stabilizing filter. Our results shed light on applying model-free PG methods to control a linear dynamical system where the state measurements could be corrupted by statistical noises and other (possibly adversarial) disturbances.

Derivative-Free Policy Optimization for Risk-Sensitive and Robust Control Design: Implicit Regularization and Sample Complexity

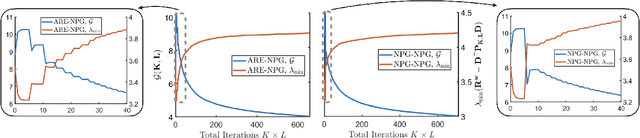
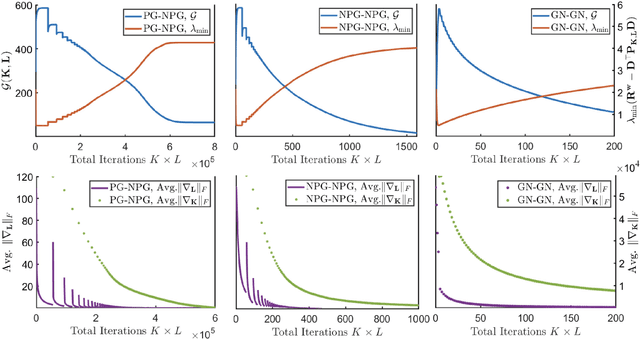
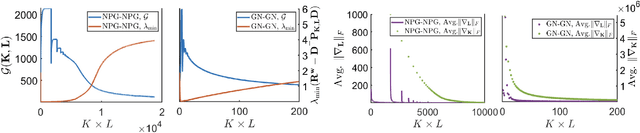
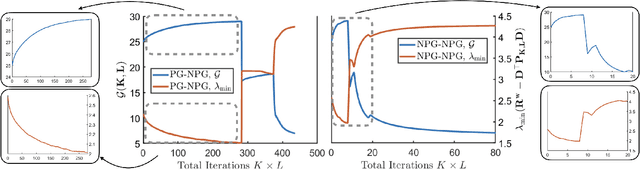
Direct policy search serves as one of the workhorses in modern reinforcement learning (RL), and its applications in continuous control tasks have recently attracted increasing attention. In this work, we investigate the convergence theory of policy gradient (PG) methods for learning the linear risk-sensitive and robust controller. In particular, we develop PG methods that can be implemented in a derivative-free fashion by sampling system trajectories, and establish both global convergence and sample complexity results in the solutions of two fundamental settings in risk-sensitive and robust control: the finite-horizon linear exponential quadratic Gaussian, and the finite-horizon linear-quadratic disturbance attenuation problems. As a by-product, our results also provide the first sample complexity for the global convergence of PG methods on solving zero-sum linear-quadratic dynamic games, a nonconvex-nonconcave minimax optimization problem that serves as a baseline setting in multi-agent reinforcement learning (MARL) with continuous spaces. One feature of our algorithms is that during the learning phase, a certain level of robustness/risk-sensitivity of the controller is preserved, which we termed as the implicit regularization property, and is an essential requirement in safety-critical control systems.

Non-Cooperative Inverse Reinforcement Learning

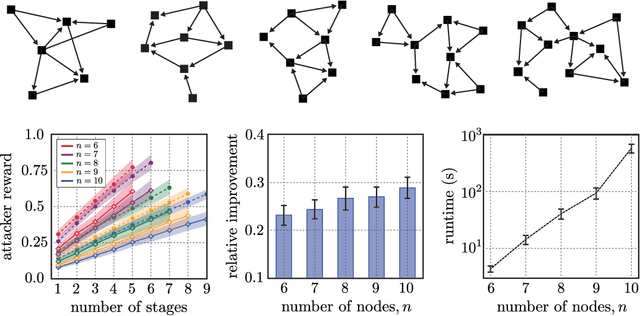
Making decisions in the presence of a strategic opponent requires one to take into account the opponent's ability to actively mask its intended objective. To describe such strategic situations, we introduce the non-cooperative inverse reinforcement learning (N-CIRL) formalism. The N-CIRL formalism consists of two agents with completely misaligned objectives, where only one of the agents knows the true objective function. Formally, we model the N-CIRL formalism as a zero-sum Markov game with one-sided incomplete information. Through interacting with the more informed player, the less informed player attempts to both infer, and act according to, the true objective function. As a result of the one-sided incomplete information, the multi-stage game can be decomposed into a sequence of single-stage games expressed by a recursive formula. Solving this recursive formula yields the value of the N-CIRL game and the more informed player's equilibrium strategy. Another recursive formula, constructed by forming an auxiliary game, termed the dual game, yields the less informed player's strategy. Building upon these two recursive formulas, we develop a computationally tractable algorithm to approximately solve for the equilibrium strategies. Finally, we demonstrate the benefits of our N-CIRL formalism over the existing multi-agent IRL formalism via extensive numerical simulation in a novel cyber security setting.