Revisiting LQR Control from the Perspective of Receding-Horizon Policy Gradient
Paper and Code
Feb 25, 2023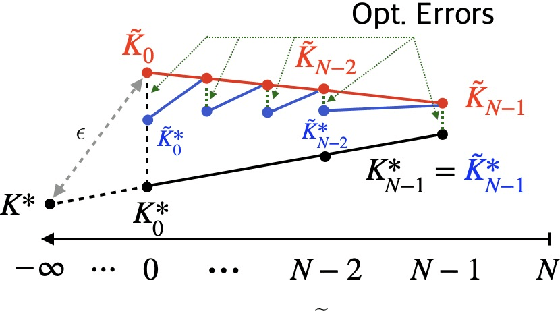
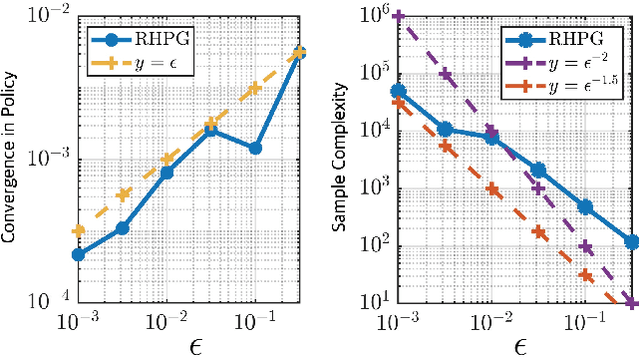
We revisit in this paper the discrete-time linear quadratic regulator (LQR) problem from the perspective of receding-horizon policy gradient (RHPG), a newly developed model-free learning framework for control applications. We provide a fine-grained sample complexity analysis for RHPG to learn a control policy that is both stabilizing and $\epsilon$-close to the optimal LQR solution, and our algorithm does not require knowing a stabilizing control policy for initialization. Combined with the recent application of RHPG in learning the Kalman filter, we demonstrate the general applicability of RHPG in linear control and estimation with streamlined analyses.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge