Task Arithmetic Through The Lens Of One-Shot Federated Learning

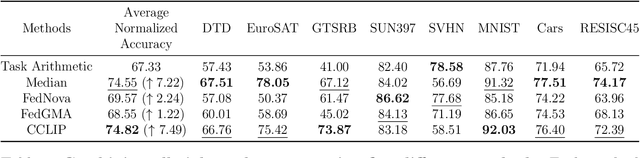
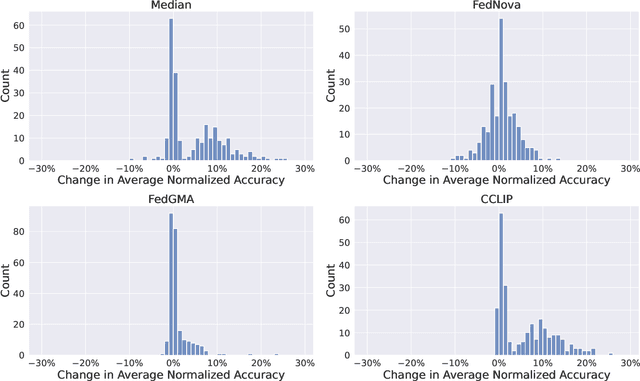
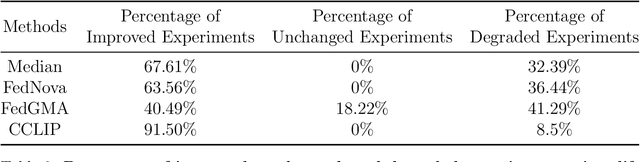
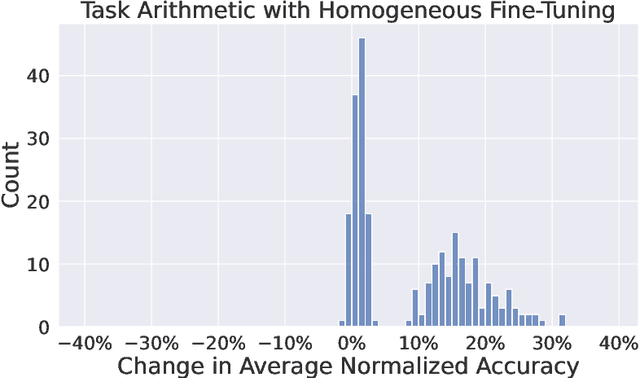
Task Arithmetic is a model merging technique that enables the combination of multiple models' capabilities into a single model through simple arithmetic in the weight space, without the need for additional fine-tuning or access to the original training data. However, the factors that determine the success of Task Arithmetic remain unclear. In this paper, we examine Task Arithmetic for multi-task learning by framing it as a one-shot Federated Learning problem. We demonstrate that Task Arithmetic is mathematically equivalent to the commonly used algorithm in Federated Learning, called Federated Averaging (FedAvg). By leveraging well-established theoretical results from FedAvg, we identify two key factors that impact the performance of Task Arithmetic: data heterogeneity and training heterogeneity. To mitigate these challenges, we adapt several algorithms from Federated Learning to improve the effectiveness of Task Arithmetic. Our experiments demonstrate that applying these algorithms can often significantly boost performance of the merged model compared to the original Task Arithmetic approach. This work bridges Task Arithmetic and Federated Learning, offering new theoretical perspectives on Task Arithmetic and improved practical methodologies for model merging.

On the Convergence of a Federated Expectation-Maximization Algorithm

Data heterogeneity has been a long-standing bottleneck in studying the convergence rates of Federated Learning algorithms. In order to better understand the issue of data heterogeneity, we study the convergence rate of the Expectation-Maximization (EM) algorithm for the Federated Mixture of $K$ Linear Regressions model. We fully characterize the convergence rate of the EM algorithm under all regimes of $m/n$ where $m$ is the number of clients and $n$ is the number of data points per client. We show that with a signal-to-noise-ratio (SNR) of order $\Omega(\sqrt{K})$, the well-initialized EM algorithm converges within the minimax distance of the ground truth under each of the regimes. Interestingly, we identify that when $m$ grows exponentially in $n$, the EM algorithm only requires a constant number of iterations to converge. We perform experiments on synthetic datasets to illustrate our results. Surprisingly, the results show that rather than being a bottleneck, data heterogeneity can accelerate the convergence of federated learning algorithms.

Byzantine-Robust Clustered Federated Learning

This paper focuses on the problem of adversarial attacks from Byzantine machines in a Federated Learning setting where non-Byzantine machines can be partitioned into disjoint clusters. In this setting, non-Byzantine machines in the same cluster have the same underlying data distribution, and different clusters of non-Byzantine machines have different learning tasks. Byzantine machines can adversarially attack any cluster and disturb the training process on clusters they attack. In the presence of Byzantine machines, the goal of our work is to identify cluster membership of non-Byzantine machines and optimize the models learned by each cluster. We adopt the Iterative Federated Clustering Algorithm (IFCA) framework of Ghosh et al. (2020) to alternatively estimate cluster membership and optimize models. In order to make this framework robust against adversarial attacks from Byzantine machines, we use coordinate-wise trimmed mean and coordinate-wise median aggregation methods used by Yin et al. (2018). Specifically, we propose a new Byzantine-Robust Iterative Federated Clustering Algorithm to improve on the results in Ghosh et al. (2019). We prove a convergence rate for this algorithm for strongly convex loss functions. We compare our convergence rate with the convergence rate of an existing algorithm, and we demonstrate the performance of our algorithm on simulated data.