Reinforcement Learning Paycheck Optimization for Multivariate Financial Goals

We study paycheck optimization, which examines how to allocate income in order to achieve several competing financial goals. For paycheck optimization, a quantitative methodology is missing, due to a lack of a suitable problem formulation. To deal with this issue, we formulate the problem as a utility maximization problem. The proposed formulation is able to (i) unify different financial goals; (ii) incorporate user preferences regarding the goals; (iii) handle stochastic interest rates. The proposed formulation also facilitates an end-to-end reinforcement learning solution, which is implemented on a variety of problem settings.

Deep PQR: Solving Inverse Reinforcement Learning using Anchor Actions

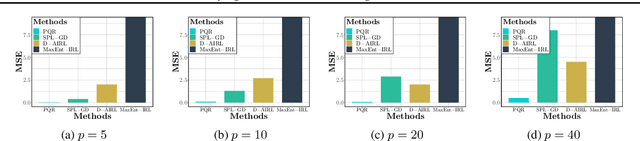
We propose a reward function estimation framework for inverse reinforcement learning with deep energy-based policies. We name our method PQR, as it sequentially estimates the Policy, the $Q$-function, and the Reward function by deep learning. PQR does not assume that the reward solely depends on the state, instead it allows for a dependency on the choice of action. Moreover, PQR allows for stochastic state transitions. To accomplish this, we assume the existence of one anchor action whose reward is known, typically the action of doing nothing, yielding no reward. We present both estimators and algorithms for the PQR method. When the environment transition is known, we prove that the PQR reward estimator uniquely recovers the true reward. With unknown transitions, we bound the estimation error of PQR. Finally, the performance of PQR is demonstrated by synthetic and real-world datasets.