Reinforcement Learning Paycheck Optimization for Multivariate Financial Goals

We study paycheck optimization, which examines how to allocate income in order to achieve several competing financial goals. For paycheck optimization, a quantitative methodology is missing, due to a lack of a suitable problem formulation. To deal with this issue, we formulate the problem as a utility maximization problem. The proposed formulation is able to (i) unify different financial goals; (ii) incorporate user preferences regarding the goals; (iii) handle stochastic interest rates. The proposed formulation also facilitates an end-to-end reinforcement learning solution, which is implemented on a variety of problem settings.

Improving Offline RL by Blending Heuristics

We propose Heuristic Blending (HUBL), a simple performance-improving technique for a broad class of offline RL algorithms based on value bootstrapping. HUBL modifies Bellman operators used in these algorithms, partially replacing the bootstrapped values with Monte-Carlo returns as heuristics. For trajectories with higher returns, HUBL relies more on heuristics and less on bootstrapping; otherwise, it leans more heavily on bootstrapping. We show that this idea can be easily implemented by relabeling the offline datasets with adjusted rewards and discount factors, making HUBL readily usable by many existing offline RL implementations. We theoretically prove that HUBL reduces offline RL's complexity and thus improves its finite-sample performance. Furthermore, we empirically demonstrate that HUBL consistently improves the policy quality of four state-of-the-art bootstrapping-based offline RL algorithms (ATAC, CQL, TD3+BC, and IQL), by 9% on average over 27 datasets of the D4RL and Meta-World benchmarks.

A Data-Driven State Aggregation Approach for Dynamic Discrete Choice Models

We study dynamic discrete choice models, where a commonly studied problem involves estimating parameters of agent reward functions (also known as "structural" parameters), using agent behavioral data. Maximum likelihood estimation for such models requires dynamic programming, which is limited by the curse of dimensionality. In this work, we present a novel algorithm that provides a data-driven method for selecting and aggregating states, which lowers the computational and sample complexity of estimation. Our method works in two stages. In the first stage, we use a flexible inverse reinforcement learning approach to estimate agent Q-functions. We use these estimated Q-functions, along with a clustering algorithm, to select a subset of states that are the most pivotal for driving changes in Q-functions. In the second stage, with these selected "aggregated" states, we conduct maximum likelihood estimation using a commonly used nested fixed-point algorithm. The proposed two-stage approach mitigates the curse of dimensionality by reducing the problem dimension. Theoretically, we derive finite-sample bounds on the associated estimation error, which also characterize the trade-off of computational complexity, estimation error, and sample complexity. We demonstrate the empirical performance of the algorithm in two classic dynamic discrete choice estimation applications.

Deep PQR: Solving Inverse Reinforcement Learning using Anchor Actions

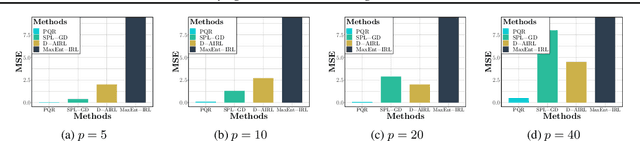
We propose a reward function estimation framework for inverse reinforcement learning with deep energy-based policies. We name our method PQR, as it sequentially estimates the Policy, the $Q$-function, and the Reward function by deep learning. PQR does not assume that the reward solely depends on the state, instead it allows for a dependency on the choice of action. Moreover, PQR allows for stochastic state transitions. To accomplish this, we assume the existence of one anchor action whose reward is known, typically the action of doing nothing, yielding no reward. We present both estimators and algorithms for the PQR method. When the environment transition is known, we prove that the PQR reward estimator uniquely recovers the true reward. With unknown transitions, we bound the estimation error of PQR. Finally, the performance of PQR is demonstrated by synthetic and real-world datasets.

Temporal Poisson Square Root Graphical Models

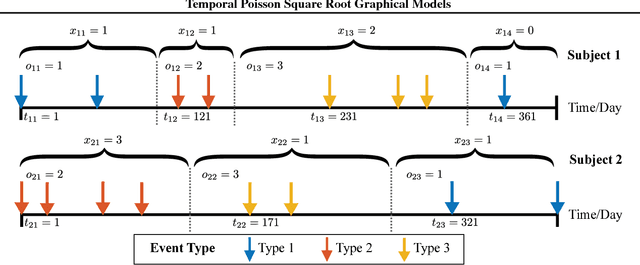
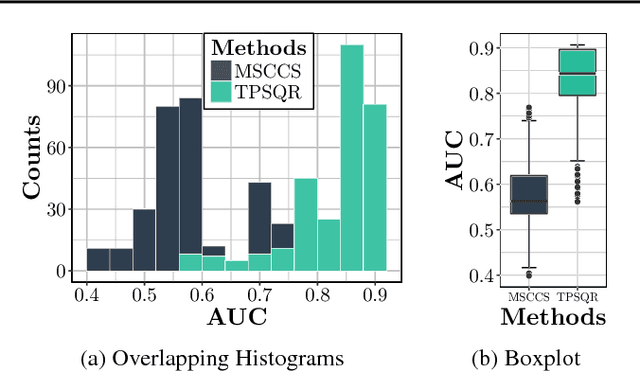
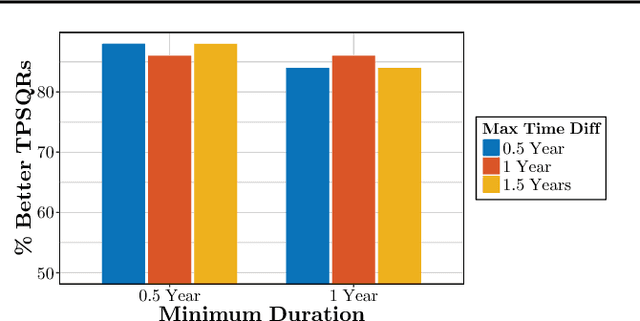
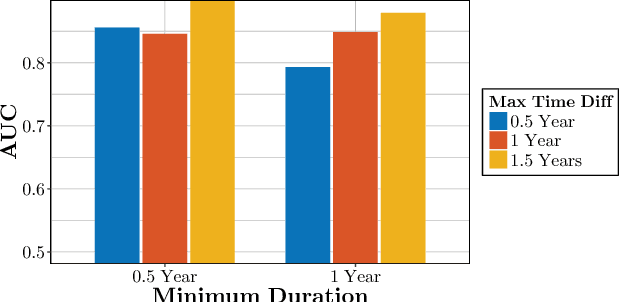
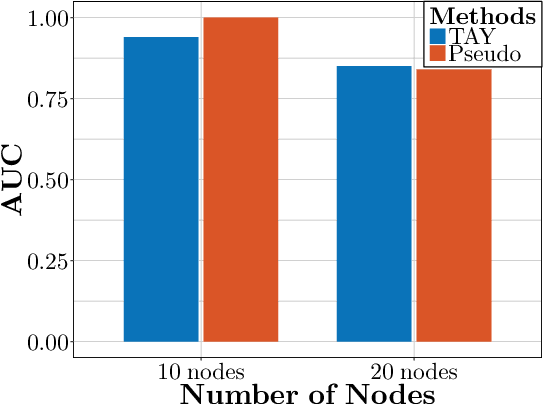
We propose temporal Poisson square root graphical models (TPSQRs), a generalization of Poisson square root graphical models (PSQRs) specifically designed for modeling longitudinal event data. By estimating the temporal relationships for all possible pairs of event types, TPSQRs can offer a holistic perspective about whether the occurrences of any given event type could excite or inhibit any other type. A TPSQR is learned by estimating a collection of interrelated PSQRs that share the same template parameterization. These PSQRs are estimated jointly in a pseudo-likelihood fashion, where Poisson pseudo-likelihood is used to approximate the original more computationally-intensive pseudo-likelihood problem stemming from PSQRs. Theoretically, we demonstrate that under mild assumptions, the Poisson pseudo-likelihood approximation is sparsistent for recovering the underlying PSQR. Empirically, we learn TPSQRs from Marshfield Clinic electronic health records (EHRs) with millions of drug prescription and condition diagnosis events, for adverse drug reaction (ADR) detection. Experimental results demonstrate that the learned TPSQRs can recover ADR signals from the EHR effectively and efficiently.

Stochastic Learning for Sparse Discrete Markov Random Fields with Controlled Gradient Approximation Error

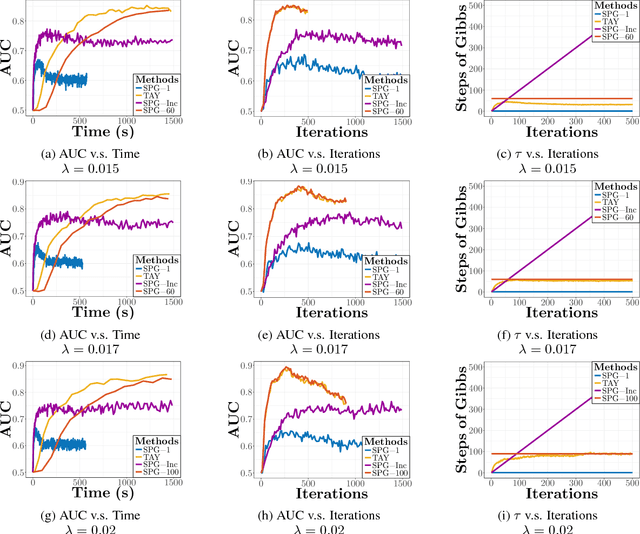
We study the $L_1$-regularized maximum likelihood estimator/estimation (MLE) problem for discrete Markov random fields (MRFs), where efficient and scalable learning requires both sparse regularization and approximate inference. To address these challenges, we consider a stochastic learning framework called stochastic proximal gradient (SPG; Honorio 2012a, Atchade et al. 2014,Miasojedow and Rejchel 2016). SPG is an inexact proximal gradient algorithm [Schmidtet al., 2011], whose inexactness stems from the stochastic oracle (Gibbs sampling) for gradient approximation - exact gradient evaluation is infeasible in general due to the NP-hard inference problem for discrete MRFs [Koller and Friedman, 2009]. Theoretically, we provide novel verifiable bounds to inspect and control the quality of gradient approximation. Empirically, we propose the tighten asymptotically (TAY) learning strategy based on the verifiable bounds to boost the performance of SPG.

Partially Linear Additive Gaussian Graphical Models

We propose a partially linear additive Gaussian graphical model (PLA-GGM) for the estimation of associations between random variables distorted by observed confounders. Model parameters are estimated using an $L_1$-regularized maximal pseudo-profile likelihood estimator (MaPPLE) for which we prove $\sqrt{n}$-sparsistency. Importantly, our approach avoids parametric constraints on the effects of confounders on the estimated graphical model structure. Empirically, the PLA-GGM is applied to both synthetic and real-world datasets, demonstrating superior performance compared to competing methods.

Joint Nonparametric Precision Matrix Estimation with Confounding

We consider the problem of precision matrix estimation where, due to extraneous confounding of the underlying precision matrix, the data are independent but not identically distributed. While such confounding occurs in many scientific problems, our approach is inspired by recent neuroscientific research suggesting that brain function, as measured using functional magnetic resonance imagine (fMRI), is susceptible to confounding by physiological noise such as breathing and subject motion. Following the scientific motivation, we propose a graphical model, which in turn motivates a joint nonparametric estimator. We provide theoretical guarantees for the consistency and the convergence rate of the proposed estimator. In addition, we demonstrate that the optimization of the proposed estimator can be transformed into a series of linear programming problems, and thus be efficiently solved in parallel. Empirical results are presented using simulated and real brain imaging data, which suggest that our approach improves precision matrix estimation, as compared to baselines, when confounding is present.

An Efficient Pseudo-likelihood Method for Sparse Binary Pairwise Markov Network Estimation

The pseudo-likelihood method is one of the most popular algorithms for learning sparse binary pairwise Markov networks. In this paper, we formulate the $L_1$ regularized pseudo-likelihood problem as a sparse multiple logistic regression problem. In this way, many insights and optimization procedures for sparse logistic regression can be applied to the learning of discrete Markov networks. Specifically, we use the coordinate descent algorithm for generalized linear models with convex penalties, combined with strong screening rules, to solve the pseudo-likelihood problem with $L_1$ regularization. Therefore a substantial speedup without losing any accuracy can be achieved. Furthermore, this method is more stable than the node-wise logistic regression approach on unbalanced high-dimensional data when penalized by small regularization parameters. Thorough numerical experiments on simulated data and real world data demonstrate the advantages of the proposed method.